PEE Moduł 8: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 677: | Linia 677: | ||
<hr width="100%"> | <hr width="100%"> | ||
NOTATKI BEZ SLAJDÓW | {| border="0" cellpadding="4" width="100%" | ||
|valign="top"|NOTATKI BEZ SLAJDÓW | |||
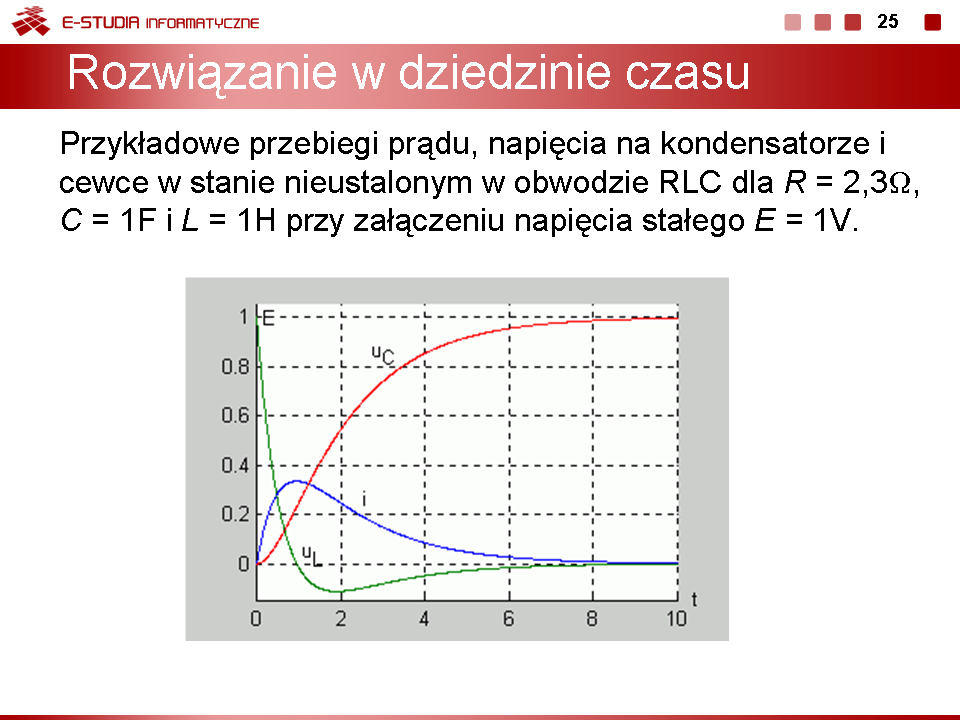
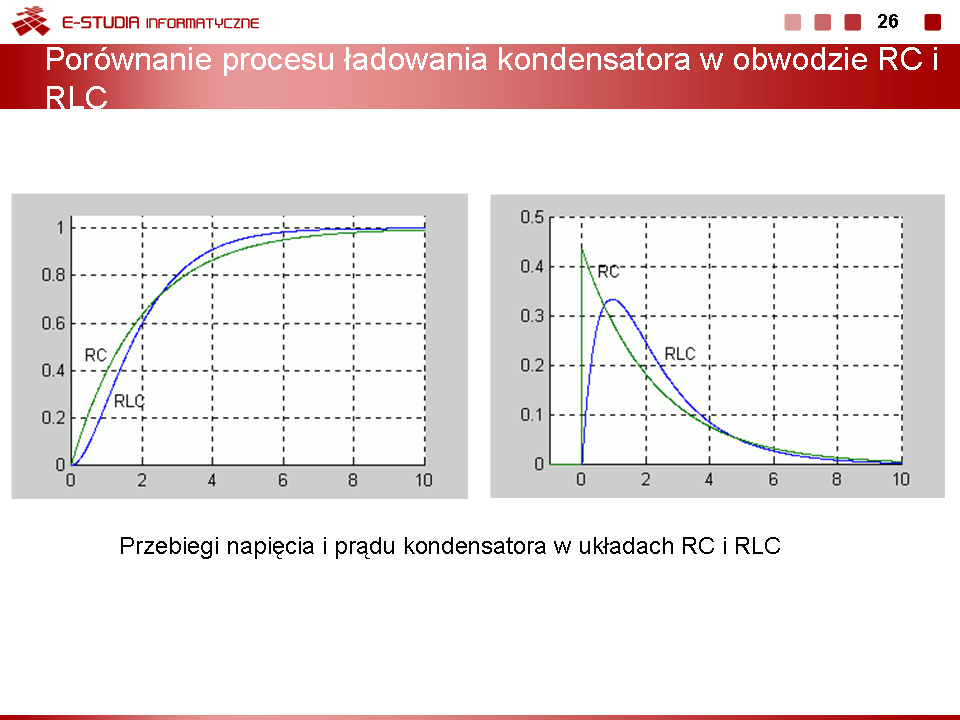
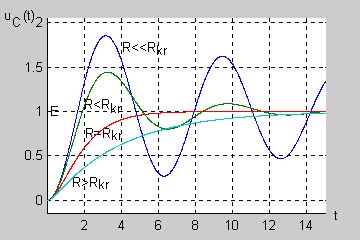
Należy podkreślić, że jakkolwiek wyrażenia analityczne opisujące przebiegi czasowe w obwodzie dla różnych przypadków tłumienia są znacznie różniące się miedzy sobą, wszystkie reprezentują charakter ciągły. Poszczególne przypadki przechodzą w siebie nawzajem przy ciągłej zmianie wartości rezystancji. Przy małej rezystancji tłumienie jest małe i przebieg prądu oraz napięć jest oscylacyjny, tłumiony wykładniczo. Wzrost wartości rezystancji powoduje wzrost tłumienia, drgania trwają krócej aż przy pewnej wartości krytycznej <math>R_{kr}=2\sqrt{\frac{L}{C}}</math> przechodzą w przebieg aperiodyczny (krytyczny), przy którym nie obserwuje się już drgań. Dalszy wzrost rezystancji niewiele zmienia w charakterze jakościowym przebiegów poza wydłużeniem stanu przejściowego. Ilustrację powyższego zjawiska na przykładzie napięcia w obwodzie przedstawiono na rys. poniższym | |||
{| | |||
|valign="top" width="500px"|[[Grafika:PEE_M8_Rtxt1.jpg]] | |||
|} | |||
'''Zadania sprawdzające''' | |||
''Zadanie 8.1'' | |||
Wyznaczyć transformatę odwrotną Laplace’a dla transmitancji operatorowej F(s) | |||
: <math>F(s)=\frac{s}{(s+2)(s+3)(s+5)^2}</math> | |||
{ | ''Rozwiązanie'' | ||
W rozważanym przypadku wszystkie bieguny są rzeczywiste, przy czym jeden z nich jest podwójny. Ich wartości są równe: <math>s_1=-2</math>, <math>s_2=-3</math>, <math>s_3=s_4=-5</math>. Najskuteczniejszą metodą pozostaje w tym przypadku metoda residuów, zgodnie z którą | |||
: <math>f(t)=res_{s \to -2}F(s)e^{st}+res_{s \to -3}F(s)e^{st}+res_{s \to -5}F(s)e^{st}</math> | |||
Wartość funkcji residuum dla poszczególnych biegunów jest równa | |||
: <math>res_{s \to -2}F(s)e^{st}=\lim_{s \to -2} F(s)(s+2)e^{st}=-\frac{2}{9}e^{-2t}</math> | |||
: <math>res_{s \to -3}F(s)e^{st}=\lim_{s \to -3} F(s)(s+3)e^{st}=\frac{3}{4}e^{-3t}</math> | |||
: <math>res_{s \to -5}F(s)e^{st}=\lim_{s \to -5} \frac{d}{ds} \left(F(s)(s+5)^2 e^{st}\right)=-\frac{19}{36}e^{-5t}-\frac{5}{6}te^{-5t}</math> | |||
Sumując poszczególne składniki otrzymujemy | |||
: <math>f(t)=-\frac{2}{9}e^{-2t}+\frac{3}{4}e^{-3t}-\frac{19}{36}e^{-5t}-\frac{5}{6}te^{-5t}</math> | |||
Zadanie 8.2 | |||
Określić przebieg napięcia na kondensatorze w stanie nieustalonym po przełączeniu metodą operatorową w obwodzie przedstawionym na rys. 8.15. Przyjąć następujące parametry obwodu:<math>R_1=50\Omega</math>, <math>R_2=100\Omega</math>, <math>C_1=10\mu F</math>, <math>C_2=20\mu F</math>, <math>e_1(t)=50V</math>, <math>e_2(t)=100V</math>. | |||
Wersja z 04:27, 2 sie 2006

|
Wykład 8. Zastosowanie metody operatorowej Laplace’a w analizie stanów nieustalonych |

|
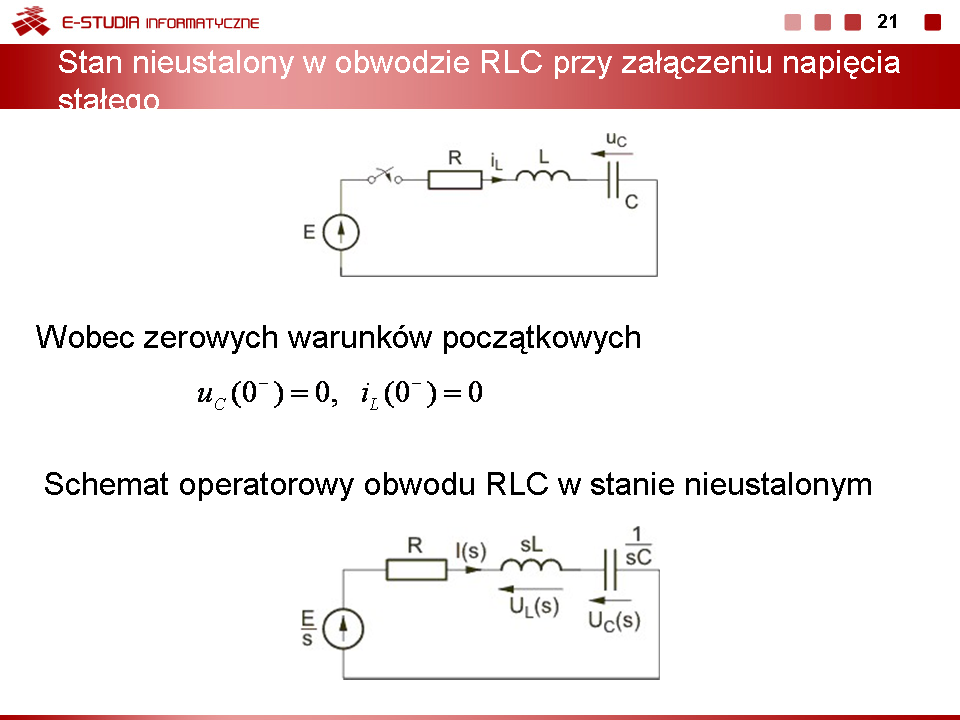
2) Stan ustalony po przełączeniu w obwodzie
(slajd 15) |
|
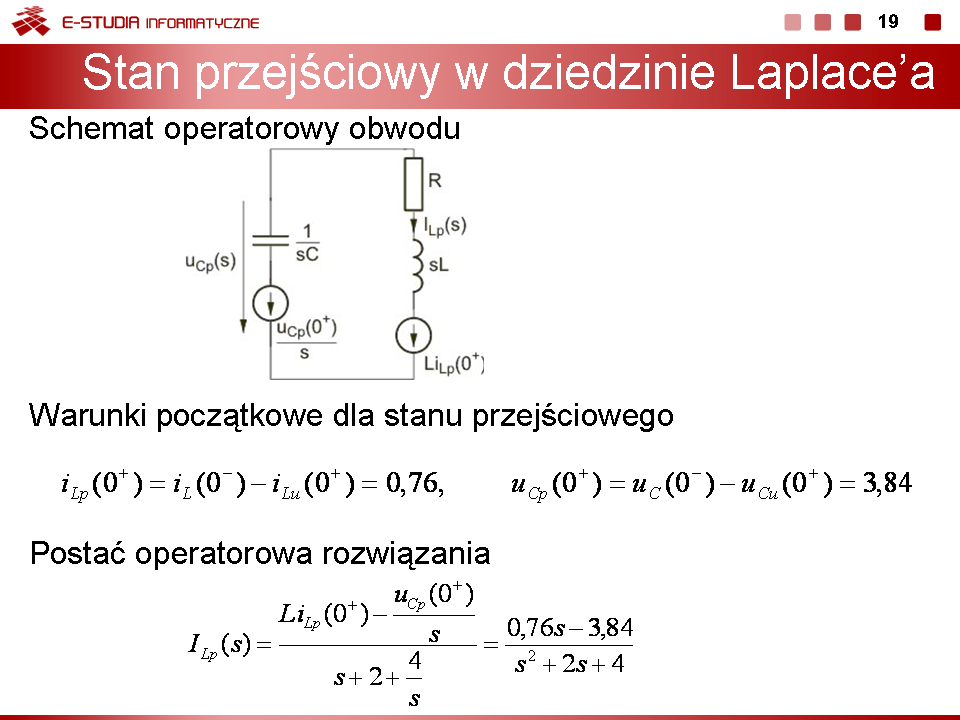
3) Stan przejściowy po przełączeniu
Schemat operatorowy przedstawiony jest na rys. na slajdzie 16 Warunki początkowe dla stanu przejściowego: |

|
Postać operatorowa rozwiązania
Wobec zespolonych biegunów zastosujemy metodę tablicową określenia transformaty odwrotnej. Zgodnie z nią
Rozwiązanie całkowite na prąd cewki w stanie nieustalonym
|

|
Przypadek aperiodyczny krytyczny
W przypadku aperiodycznym krytycznym, wobec spełnienia relacji oba pierwiastki mianownika są równe i transformata prądu wyraża się wzorem |