PEE Moduł 8: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 382: | Linia 382: | ||
Należy podkreślić, że rozbicie stanu nieustalonego na ustalony i przejściowy jest zalecane jedynie przy istnieniu wymuszeń sinusoidalnych w obwodzie po przełączeniu. Jeśli źródła takie nie występują schemat operatorowy może dotyczyć obwodu całkowitego, bez rozbijania go na schemat dla składowej ustalonej i przejściowej. W takim przypadku pozostawia się zewnętrzne źródła wymuszające w obwodzie przyjmując ich model operatorowy, czyli zastępując postać czasową źródła (wartość stała A przy wymuszeniu stałym) przez funkcję <math>\frac{A}{s}</math>. Warunki początkowe również nie podlegają modyfikacji, co oznacza, że <math>i_L(0^{+})=i_L(0^{-})</math> oraz <math>u_C(0^{+})=u_C(0^{-})</math> . | Należy podkreślić, że rozbicie stanu nieustalonego na ustalony i przejściowy jest zalecane jedynie przy istnieniu wymuszeń sinusoidalnych w obwodzie po przełączeniu. Jeśli źródła takie nie występują schemat operatorowy może dotyczyć obwodu całkowitego, bez rozbijania go na schemat dla składowej ustalonej i przejściowej. W takim przypadku pozostawia się zewnętrzne źródła wymuszające w obwodzie przyjmując ich model operatorowy, czyli zastępując postać czasową źródła (wartość stała A przy wymuszeniu stałym) przez funkcję <math>\frac{A}{s}</math>. Warunki początkowe również nie podlegają modyfikacji, co oznacza, że <math>i_L(0^{+})=i_L(0^{-})</math> oraz <math>u_C(0^{+})=u_C(0^{-})</math>. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd14.png]] | |||
|valign="top"|''Przykład '' | |||
Określić prąd cewki w stanie nieustalonym po przełączeniu w obwodzie przedstawionym na slajdzie 14. Przyjąć następujące wartości parametrów obwodu: <math>R=2\omega</math>, <math>L=1H\,</math>, <math>C=1/4F\,</math>. Zakładamy, że przełączanie zapewnia ciągłość prądu cewki podlegającej przełączeniu. | |||
Rozwiązanie | |||
1) Warunki początkowe w obwodzie: | |||
: <math>\omega=4</math> | |||
: <math>I_L=\frac{10e^{j45^\circ}}{4+j4}=\frac{2,5}{\sqrt{2}}</math> | |||
: <math>i_L(t)=2,5sin(4t)</math> | |||
: <math>i_L(0^{-})=0</math> | |||
: <math>u_C(0^{-})=0</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd15.png]] | |||
|valign="top"|2) Stan ustalony po przełączeniu w obwodzie | |||
(slajd 15) | |||
: <math>I_{Lu}=\frac{10e^{j45^\circ}}{2+j4-j1}=2,77e^{-j11,31^\circ}</math> | |||
: <math>U_{Cu}=-j1\cdot I_{Lu}=2,77e^{-j101,31^\circ}</math> | |||
: <math>i_{Lu}(t)=2,77\sqrt{2}sin(4t-11,31^\circ)</math> | |||
: <math>u_{Cu}(t)=2,77\sqrt{2}sin(4t-101,31^\circ)</math> | |||
: <math>i_{Lu}(0^{+})=-0,76</math> | |||
: <math>u_{Cu}(0^{+})=-3,84</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd16.png]] | |||
|valign="top"|3) Stan przejściowy po przełączeniu | |||
Schemat operatorowy przedstawiony jest na rys. na slajdzie 16 | |||
Warunki początkowe dla stanu przejściowego: | |||
: <math>i_{Lp}(0^{+})=i_L(0^{-})-i_{Lu}(0^{+})=0,76</math> | |||
: <math>u_{Cp}(0^{+})=u_C(0^{-})-u_{Cu}(0^{+})=3,84</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd17.png]] | |||
|valign="top"|Postać operatorowa rozwiązania | |||
<math>I_{Lp}(s)=\frac{Li_{Lp}(0^{+})-\frac{u_{Cp}(0^{+})}{s}}{s+2+\frac{4}{s}}=\frac{0,76s-3,84}{s^2+2s+4}</math> | |||
Wobec zespolonych biegunów zastosujemy metodę tablicową określenia transformaty odwrotnej. Zgodnie z nią | |||
<math>I_{Lp}(s)=\frac{0,76(s+1)-4,6 \cdot \frac{1}{\sqrt{3}}\sqrt{3}}{(s+1)^2+(\sqrt{3})^2}</math> | |||
<math>i_{Lp}(t)=0,76e^{-t}cos(\sqrt{3}t)-2,67e^{-t}sin(\sqrt{3}t)</math> | |||
Rozwiązanie całkowite na prąd cewki w stanie nieustalonym | |||
<math>i_L(t)=i_{Lu}(t)+i_{Lp}(t)=</math> | |||
<math>=2,77\sqrt{2}sin(4t-11,31^\circ)+0,76e^{-t}cos(\sqrt{3}t)-2,67e^{-t}sin(\sqrt{3}t)</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd18.png]] | |||
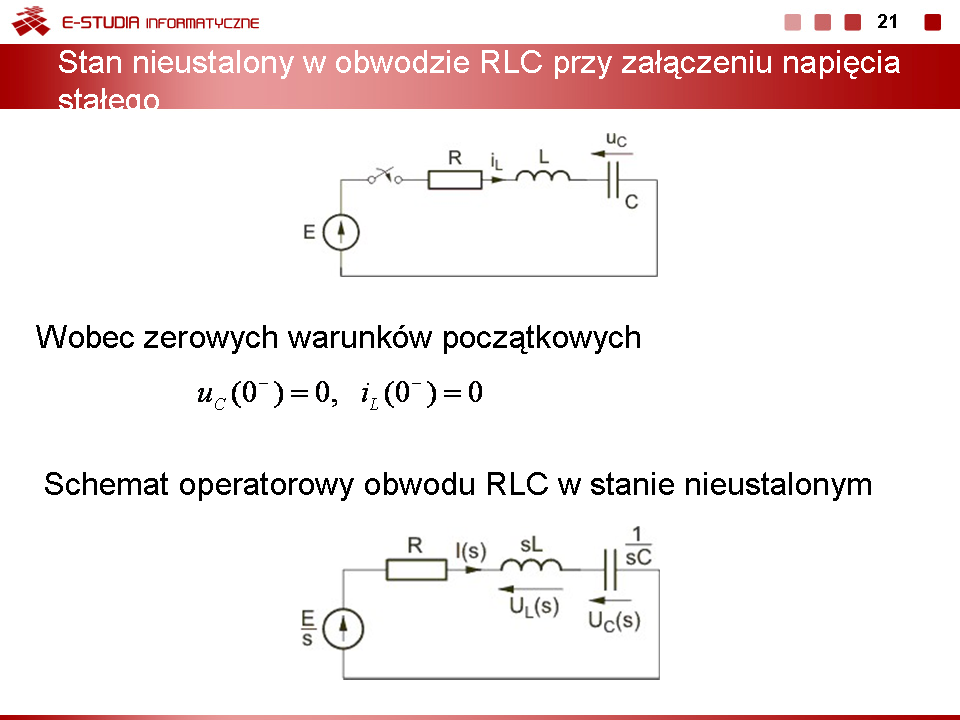
|valign="top"|'''Stan nieustalony w obwodzie RLC przy załączeniu napięcia stałego''' | |||
'''Rozwiązanie operatorowe''' | |||
Rozpatrzmy załączenie napięcia stałego E do gałęzi szeregowej RLC przedstawionej na rys. pierwszym na slajdzie 18. | |||
Wobec zerowych warunków początkowych (brak wymuszenia w obwodzie przed przełączeniem) mamy <math>u_C(0^{-})=0</math>, <math>i_L(0^{-})=0</math>. | |||
Schemat operatorowy obwodu w stanie nieustalonym przedstawiony jest na rys. drugim na slajdzie 18. Warunki początkowe napięcia kondensatora i prądu cewki określają równania | |||
: <math>u_C(0^{+})=u_C(0^{-})=0</math> | |||
: <math>i_L(0^{+})=i_L(0^{-})=0</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd19.png]] | |||
|valign="top"|Z prawa napięciowego Kirchhoffa zastosowanego do obwodu wynika następująca postać operatorowa prądu cewki | |||
<math>I(s)=\frac{E/s}{sL+R+1/sC}=\frac{E/L}{s^2+\frac{R}{L}s+\frac{1}{LC}}</math> | |||
Dla wyznaczenia transformaty odwrotnej należy obliczyć pierwiastki mianownika transmitancji, czyli | |||
: <math>s^2+\frac{R}{L}s+\frac{1}{LC}=0</math> | |||
W wyniku rozwiązania tego równania otrzymuje się dwa pierwiastki (bieguny układu) | |||
: <math>s_1=-\frac{R}{2L}+\sqrt{(\frac{R}{2L})^2-\frac{1}{LC}}</math> | |||
: <math>s_2=-\frac{R}{2L}-\sqrt{(\frac{R}{2L})^2-\frac{1}{LC}}</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd20.png]] | |||
|valign="top"|Z postaci wzoru opisującego bieguny wynika, że w zależności od znaku funkcji podpierwiastkowej możliwe są 3 przypadki rozwiązania. | |||
* Przypadek '''aperiodyczny''' dla <math>R>2\sqrt{\frac{L}{C}}</math>. Przy spełnieniu tego warunku oba bieguny są rzeczywiste i ujemne. Charakter zmian prądu w obwodzie w stanie przejściowym jest aperiodyczny (nieokresowy) zanikający do zera w sposób wykładniczy. | |||
* Przypadek '''aperiodyczny krytyczny''' występujący dla <math>R=2\sqrt{\frac{L}{C}}</math>. Przy spełnieniu tego warunku oba bieguny są rzeczywiste i równe sobie. Charakter zmian prądu w obwodzie w stanie przejściowym jest również aperiodyczny, podobnie jak w przypadku pierwszym, ale czas dochodzenia do wartości ustalonych (z określona tolerancją) jest najkrótszy z możliwych. | |||
* Przypadek '''oscylacyjny''' (periodyczny) występujący dla <math>R<2\sqrt{\frac{L}{C}}</math>. Przy spełnieniu tego warunku oba bieguny są zespolone (zespolony i sprzężony z nim). Charakter zmian prądu w obwodzie w stanie przejściowym jest sinusoidalny tłumiony, o oscylacjach zanikających do zera. | |||
Rezystancja <math>R=2\sqrt{\frac{L}{C}}</math> nazywana jest rezystancją krytyczną i oznaczana w postaci <math>R_{kr}</math>. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd21.png]] | |||
|valign="top"|'''Przypadek aperiodyczny''' | |||
Rozpatrzymy najpierw przypadek pierwszy (aperiodyczny). Ze względu na to, że oba bieguny są rzeczywiste w obliczeniach transformaty odwrotnej najwygodniej jest zastosować metodę residuów. Zgodnie z nią przebieg czasowy prądu <math>i(t)</math> można zapisać w postaci | |||
Wersja z 01:45, 2 sie 2006

|
Wykład 8. Zastosowanie metody operatorowej Laplace’a w analizie stanów nieustalonych |

|
2) Stan ustalony po przełączeniu w obwodzie
(slajd 15) |
|
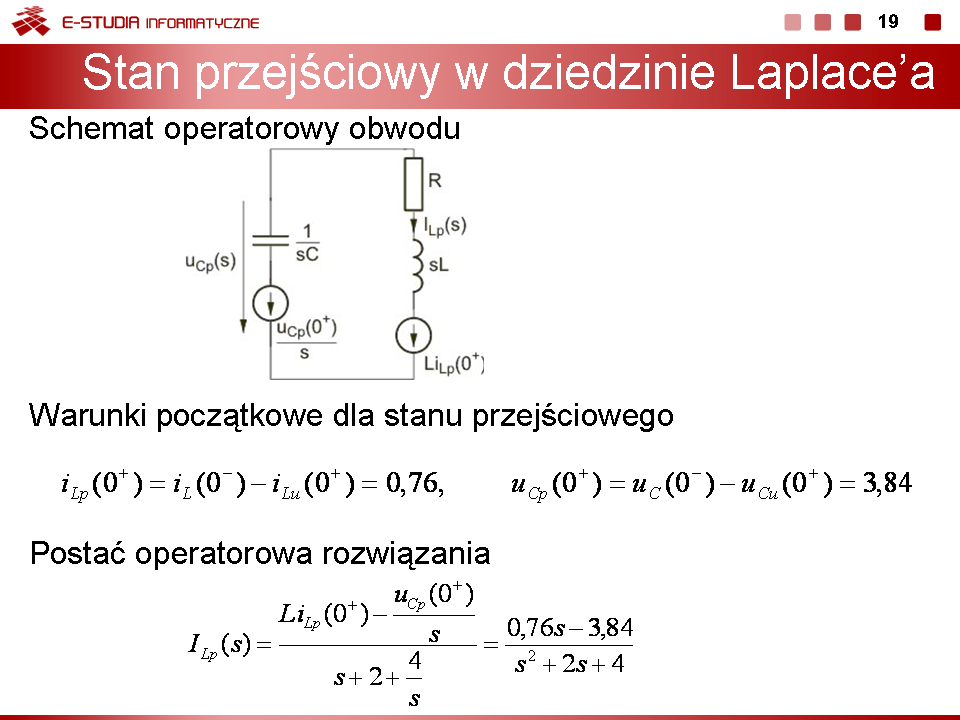
3) Stan przejściowy po przełączeniu
Schemat operatorowy przedstawiony jest na rys. na slajdzie 16 Warunki początkowe dla stanu przejściowego: |

|
Postać operatorowa rozwiązania
Wobec zespolonych biegunów zastosujemy metodę tablicową określenia transformaty odwrotnej. Zgodnie z nią
Rozwiązanie całkowite na prąd cewki w stanie nieustalonym
|