Języki, automaty i obliczenia/Wykład 1: Słowa, katenacja - elementy teorii półgrup, półgrupy i monoidy wolne

Definicje, oznaczenia i podstawowe własności

Przyjmijmy, że $\mathbb{\mathbb{N}}=\{1,2,\dots \}$ oznacza zbiór liczb naturalnych, a ${\mathbb{\mathbb{N}}}_0$ zbiór liczb naturalnych wraz z 0. Przypomnimy teraz podstawowe wiadomości z wykładu Algebra Liniowa dotyczące struktur algebraicznych, a dokładniej struktur najprostszych, półgrup i monoidów, posiadających jedno tylko działanie.

Definicja 1.1

Zbiór $S$, w którym określone jest działanie łączne, to znaczy spełniające warunek

$\mathrm{\forall }x,y,z\in Sx\cdot (y\cdot z)=(x\cdot y)\cdot z$

nazywamy półgrupą.

Przykład 1.1

Zbiór liczb naturalnych z dodawaniem $(\mathbb{\mathbb{N}},+)$ tworzy półgrupę.

Definicja 1.2

Półgrupę $M$, w której istnieje element neutralny działania, to znaczy element $1_M\in M$ spełniający warunek

$\mathrm{\forall }x\in M{1}_M\cdot x=x\cdot 1_M=x$

nazywamy monoidem.

Przykład 1.2

(1) Zbiór liczb naturalnych z mnożeniem $(\mathbb{\mathbb{N}},\cdot ,1)$ jest monoidem.

(2) Zbiór liczb naturalnych z zerem $({\mathbb{\mathbb{N}}}_0,+,0)$ jest monoidem ze względu na dodawanie.

(3) Monoidem jest $(A^A,\circ ,i{d}_A)$ - zbiór odwzorowań dowolnego zbioru $A$ w siebie ze składaniem jako działaniem i identycznością jako elementem neutralnym.

Dwa pierwsze monoidy są przemienne, czyli działanie jest przemienne, a trzeci jest nieprzemienny.

Każdy monoid jest półgrupą.

Dla uproszczenia notacji będziemy opuszczać kropkę "$\cdot$" oznaczającą działanie oraz używać nazwy "jedynka" na element neutralny. Jeśli nie będzie zaznaczone inaczej, to $(\mathbf{𝐒},\cdot )$ będzie oznaczać półgrupę, a $(\mathbf{𝐌},\cdot ,1_{\mathbf{𝐌}})$ monoid. Ze względu na łączność działania zarówno w półgrupie, jak i w monoidzie iloczyn $x_1...x_n$, a także $x^n=x...x$ (n razy) jest określony jednoznacznie bez potrzeby wprowadzania nawiasów. Dla dowolnych liczb naturalnych $m,n\in \mathbb{\mathbb{N}}$ zachodzą wzory

$\begin{array}{c}{x}^{m+n}=x^m{x}^n=x^n{x}^m,\\ (x^m{)}^n=x^{mn}.\end{array}$

Dla dowolnego

$x\in M$

przyjmujemy z definicji

$x^0=1_M$.

Strukturę monoidu $M$ przenosimy na zbiór potęgowy ${𝒫}(M)$ wszystkich podzbiorów monoidu $M$, określając dla dowolnych $A,B\in {𝒫}(M)$ działanie

$A\cdot B=\{x\in \mathbf{𝐌}:\mathrm{\exists }a\in A,\mathrm{\exists }b\in B,x=ab\}$

$({𝒫}(M),\cdot ,\{1_M\})$ jest monoidem.
Podobnie przenosimy strukturę półgrupy z $S$ na ${𝒫}(S)$.
Dla dowolnego podzbioru monoidu (półgrupy) i dla dowolnej liczby $n\in \mathbb{\mathbb{N}}$ zapis $A^n$ oznacza n-krotny iloczyn zbioru $\text{A}$ przez siebie rozumiany w powyższym sensie.
W szczególności $A^1=A$

W przypadku monoidu przyjmujemy z definicji

$A^0=\{1_M\}$.

Definicja 1.3

Homomorfizmem półgrup $(S,\cdot ),(S^{\prime },*)$ nazywamy odwzorowanie

$h:S⟼S^{\prime }$ takie, że $\mathrm{\forall }x,y\in Sh(x\cdot y)=h(x)*h(y)$.

Homomorfizmem monoidów $(M,\cdot ,1_M),(M^{\prime },*,1_{M^{\prime }})$ nazywamy odwzorowanie $h:M⟼M^{\prime }$

takie, że $\mathrm{\forall }x,y\in Mh(x\cdot y)=h(x)*h(y)ih(1_M)=1_{M^{\prime }}$.

Przykład 1.3

Odwzorowanie $h:{\mathbb{\mathbb{Z}}}_{mod3}⟶{\mathbb{\mathbb{Z}}}_{mod6}$ takie, że

$\begin{array}{c}\begin{array}{l}1⟶4\\ 0⟶0\\ 2⟶2\end{array}\end{array}$

jest homomorfizmem półgrupy $({\mathbb{\mathbb{Z}}}_{mod3},\cdot )$ w półgrupę $({\mathbb{\mathbb{Z}}}_{mod6},\cdot )$, ale nie jest homomorfizmem monoidu $({\mathbb{\mathbb{Z}}}_{mod3},\cdot ,1)$ w monoid $({\mathbb{\mathbb{Z}}}_{mod6},\cdot ,1)$, bo wartością 1 z monoidu $({\mathbb{\mathbb{Z}}}_{mod3},\cdot ,1)$ nie jest jedynka monoidu $({\mathbb{\mathbb{Z}}}_{mod6},\cdot ,1)$.

Dla zainteresowanych

Definicja 1.4.

Niech $(S,\cdot ),(M,\cdot ,1_M)$ będą odpowiednio dowolną półgrupą, monoidem.

• $(T,\cdot )$ nazywamy podpółgrupą $S$ wtedy i tylko wtedy, gdy $T\subset S$ i $T^2\subset T$.

• $(N,\cdot ,1_M)$ nazywamy podmonoidem $M$ wtedy i tylko wtedy, gdy $N$ jest podpółgrupą $M$ i $1_M\in N$

Przykład 1.4.

$({\mathbb{\mathbb{Z}}}_{mod6},\cdot )$ jest monoidem. Podzbiór $\{2,4\}$, jako zamknięty na działanie ${\cdot }_{mod6}$, tworzy podpółgrupę ${\mathbb{\mathbb{Z}}}_{mod6}$. $(\{2,4\},{\cdot }_{mod6})$ jest monoidem z $4$ jako elementem neutralnym, ale nie podmonoidem ${\mathbb{\mathbb{Z}}}_{mod6}$.

Niech $X$ będzie dowolnym podzbiorem monoidu $M$. Zbiór

$X^{*}=\{1\}\cup X\cup X^2\cup ...\cup X^n\cup \dots =\bigcup _{i=0}^{\mathrm{\infty }}{X}^i$

jest podmonoidem monoidu $M$. Jest to najmniejszy, w sensie inkluzji podmonoid monoidu $M$ zawierający zbiór $X$. Gdy spełniona jest równość $X^{*}=M$, to mówimy, że $X$ jest zbiorem generatorów monoidu $M$. Zachodzą następujące własności:

1. Zbiór generatorów nie jest wyznaczony jednoznacznie.

2. Dla dowolnego monoidu istnieje zbiór generatorów, jest nim w szczególności zbiór $M$.

Podobnie dla dowolnego podzbioru $X$ półgrupy $S$ zbiór

$X^{+}=X\cup X^2\cup ...\cup X^n\cup \dots =\bigcup _{i=1}^{\mathrm{\infty }}{X}^i$

jest podpółgrupą $S$ i to najmniejszą w sensie inkluzji zawierającą zbiór $X$.
Powyższe uwagi dotyczące zbioru generatorów monoidów przenoszą się odpowiednio dla półgrup.

Przykład 1.5.

W monoidzie $({\mathbb{\mathbb{N}}}_0,+,0)$ podmonoid generowany przez zbiór generatorów $X=\{2\}$ składa się z liczb parzystych i nieujemnych.

Definicja 1.5

Niech $S$ będzie półgrupą. Relację równoważności $\rho \subset S^2$ nazywamy:

(1) prawą kongruencją w półgrupie $S$, jeśli $\mathrm{\forall }x,y,z\in Sx\rho y\Rightarrow xz\rho yz$,

(2) lewą kongruencją w półgrupie $S$, jeśli $\mathrm{\forall }x,y,z\in Sx\rho y\Rightarrow zx\rho zy$,

(3) kongruencją, jeśli jest prawą i lewą kongruencją, tzn. $\mathrm{\forall }x,y,z\in Sx\rho y\Rightarrow zx\rho zyixz\rho yz$.

Zastępując w powyższej definicji półgrupę $S$ na monoid $M$ otrzymamy dualnie pojęcia prawej kongruencji, lewej kongruencji i kongruencji zdefiniowane w monoidzie.
Mając kongruencję $\rho$ określoną w półgrupie $S$ (monoidzie $M)$ możemy utworzyć półgrupę ilorazową $S/\rho$ (monoid ilorazowy $M/\rho$), której elementami są klasy równoważności (abstrakcji) relacji $\rho$.

Dla dowolnego homomorfizmu półgrup $h:S⟼S^{\prime }$ określamy relację

$Ke{r}_h=\{(x,y)\in S\times S:h(x)=h(y)\}$. Relacja $Ke{r}_h$ jest kongruencją w półgrupie $S$.

Dla homomorfizmu monoidów $h:M⟼M^{\prime }$ relacja $Ke{r}_h$ jest kongruencją w monoidzie $M$.

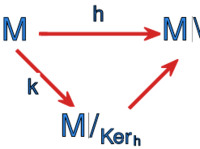
Podstawowe twierdzenie o epimorfizmie dla struktur algebraicznych przyjmuje dla półgrup i odpowiednio dla monoidów następującą postać.

Twierdzenie 1.1

Niech $h:S⟼S^{\prime }$ będzie dowolnym epimorfizmem półgrupy $S$ na półgrupę $S\text{'}$. Półgrupa $S\text{'}$ jest izomorficzna z półgrupą ilorazową $S{/}_{Ke{r}_h}$.

<flash>file=Ja-1-1.swf|width=200|height=200</flash> <div.thumbcaption>Rysunek 1

Twierdzenie 1.2

Niech $h:M⟼M^{\prime }$ będzie dowolnym epimorfizmem monoidu $M$ na monoid $M\text{'}$. Monoid $M\text{'}$ jest izomorficzny z monoidem ilorazowym $M{/}_{Ke{r}_h}$.

Rysunek 2

Półgrupy wolne i monoidy wolne

Niech $A$ oznacza dowolny zbiór.

Definicja 2.1

Wolnym monoidem $A^{*}$ o bazie $A$ nazywamy zbiór wszystkich skończonych ciągów:

$A^{*}=\{(a_1,...,a_n):n\ge 0,a_i\in A\}$ wraz z działaniem $(a_1,...,a_n)\cdot (b_1,...,b_m)=(a_1,...,a_n,b_1,...,b_m)$

Ciąg pusty $(n=0)$ oznaczamy symbolem "1" i z definicji jest on elementem neutralnym określonego powyżej działania, nazywanego katenacją lub konkatenacją.

Przyjmujemy następującą konwencję zapisu: $(a)\equiv a,(a_1,...,a_n)\equiv a_1...a_n$. W oparciu o nią możemy stwierdzić inkluzję $A\subset A^{*}$.

Dla zainteresowanych

Ta inkluzja uzasadnia użycie wprowadzonego wcześniej oznaczenia $A^{*}$.
$A^{*}$ jest najmniejszym podmonoidem monoidu $A^{*}$ zawierającym $A$.

Definicja 2.2

Wolną półgrupą $A^{+}$ nad alfabetem $A$ nazywamy zbiór wszystkich skończonych ciągów:

$A^{+}=\{(a_1,...,a_n):n>0,a_i\in A\}$ wraz z działaniem katenacji.

Używa się także określeń - wolny monoid o bazie $A$ i wolna półgrupa o bazie $A$.

• Elementy alfabetu $A$ nazywamy literami.

• Elementy wolnego monoidu (półgrupy) nazywamy słowami i oznaczać bedziemy w wykładzie najczęściej literami $u,v,w$.

• Dowolny podzbiór wolnego monoidu (półgrupy) nazywamy językiem.

Długością słowa $w\in A^{*}$ nazywamy liczbę $|w|$ będącą długością ciągu określającego to słowo. Słowo puste 1, czyli odpowiadające ciągowi pustemu ma długość równą 0.

Przykład 2.1

(1) Wolna półgrupa $\{0,1{\}}^{+}$ składa się z ciągów binarnych.

(2) Wolny monoid $\{0,1{\}}^{*}$ składa się z ciągów binarnych i ciągu pustego.

Definicja 2.3

Niech $A$ i $B$ będą alfabetami. Podstawieniem nazywamy homomorfizm

$s:A^{*}⟶{𝒫}(B^{*})$. Odwzorowanie $s$ jako homomorfizm monoidu $A^{*}$ w monoid ${𝒫}(B^{*})$ spełnia dla dowolnych $v,w\in A^{*}$ równość $s(vw)=s(v)s(w)\text{oraz}s(1)=\{1\}$

Dla zainteresowanych

Twierdzenie 2.1.

Niech $A$ oznacza dowolny zbiór, a $(M,\cdot ,1_M)$ dowolny monoid.

(1) Każde odwzorowanie

$f:A⟼M$

daje się jednoznacznie rozszerzyć do homomorfizmu $h:A^{*}⟼M$.

(2) Homomorfizm $h$ jest epimorfizmem wtedy i tylko wtedy, gdy $f(A)$ jest zbiorem generatorów $M$.

Dowód

(1) Przyjmujemy

$\mathrm{\forall }{a}_1...a_n\in A^{+}h(a_1...a_n)=f(a_1)...f(a_n)\text{oraz}h(1)=1_M$.

Tak określone $h$ jest jedynym rozszerzeniem przekształcenia $f$.

(2) $f(A{)}^{*}=M\iff \mathrm{\forall }s\in Ms=f(a_1)...f(a_n)=h(a_1...a_n)$ dla pewnego $a_1...a_n\in A^{*}\iff h$ jest suriekcją.

Przyjmując w powyższym twierdzeniu jako $A$ dowolny zbiór generatorów monoidu $M$ oraz jako funkcję $f$ włożenie $i{d}_A:A⟶\mathbf{𝐌}$ równe identyczności na $A$ dochodzimy do następującego wniosku.

Wniosek 2.1.

Każdy monoid $M$ jest homomorficznym obrazem wolnego monoidu $A^{*}$ utworzonego nad dowolnym zbiorem generatorów $M$.

Udowodnione powyżej twierdzenie oraz sformułowany wniosek prawdziwy jest również dla półgrup.
Powyższe rezultaty określają rolę wolnych monoidów (półgrup) w klasie wszystkich monoidów (półgrup).

Twierdzenie 2.2.

Monoid $M$ jest wolny wtedy i tylko wtedy, gdy każdy element $m\in S=M\setminus \{1\}$ ma jednoznaczny rozkład na elementy zbioru $A=S\setminus S^2$.

Dowod

Załóżmy, że monoid $M$ jest wolny, to znaczy $M=B^{*}$ dla pewnego zbioru (bazy) $B$.

• Udowodnimy, że $A$ jest zbiorem generatorów monoidu $M$. W tym celu wykażemy, że zachodzi inkluzja $S\subset (S\setminus S^2{)}^{+}$. Dowód przeprowadzimy nie wprost. Załóżmy więc, że

$S\setminus (S\setminus S^2{)}^{+}\ne \mathrm{\varnothing }$

i niech $m$ oznacza element z tego zbioru o najmniejszej długości w $B^{*}$.
Wnioskujemy stąd kolejno:

$m\notin (S\setminus S^2{)}^{+}$
$m\in S^2$
$m=s_1{s}_2$ dla pewnych $s_1,s_2\in S$,

przy czym długość $s_1,s_2$ jest silnie mniejsza niż długość $m$. Zatem

$s_1,s_2\in (S\setminus S^2{)}^{+}$

a to oznacza, że

$m=s_1{s}_2\in (S\setminus S^2{)}^{+}$

Otrzymana sprzeczność kończy dowód faktu, że $A=S\setminus S^2$ jest zbiorem generatorów monoidu $M$.

• Pokażemy teraz, że $A\subset B$.
  Niech $m=b_1...b_k\in S\setminus S^2$ dla pewnych $b_i\in B$, $i=1,...,k$.
  Jeśli $k>1$, to $m\in S^2$, co jest sprzeczne z wyborem $m$. Zatem $k=1$, co implikuje $A\subset B$.

Z definicji wolnego monoidu wynika jednoznaczność rozkładu na elementy z bazy $B$, a to pociąga za sobą jednoznaczność rozkładu na elementy z podzbioru $A=S\setminus S^2$.

Niech teraz $M$ oznacza monoid z jednoznacznością rozkładu na elementy zbioru $A=S\setminus S^2$. Rozszerzamy identyczność $i{d}_A:A⟼M$ do homomorfizmu $h:A^{*}⟼M$. Z założenia wynika, że każdy element $m\in S$ można przedstawić jako iloczyn

$m=a_1...a_{n}gdzie{a}_i\in Adlai=1,...,n$.

Zatem

$h(a_1...a_n)=h(a_1)...h(a_n)a_1...a_n$.

Homomorfizm $h$ jest izomorfizmem, więc monoid $M$ jako izomorficzny z $A^{*}$ jest wolny.

Powyższe twierdzenie posiada swój odpowiednik dla wolnych półgrup.

Twierdzenie 2.3.

Półgrupa $S$ jest wolna wtedy i tylko wtedy, gdy każdy element $x\in S$ ma jednoznaczny rozkład na elementy zbioru $S\setminus S^2$.

Wniosek 2.2.

Baza wolnego monoidu (półgrupy) jest minimalym zbiorem generatorów.

Przyklad 2.2.

(1) Półgrupa $(\mathbb{\mathbb{N}},+)$ jest wolna. Każdy jej element można jednoznacznie zapisać jako sumę jedynek - $\mathbb{\mathbb{N}}\setminus (\mathbb{\mathbb{N}}+\mathbb{\mathbb{N}})=\left\{1\right\}$.

(2) Dla ${\mathbb{\mathbb{N}}}_2=\{n\in \mathbb{\mathbb{N}}:n\ge 2\}$ półgrupa $({\mathbb{\mathbb{N}}}_2,+)$ nie jest to półgrupą wolną.
Nie ma jednoznaczności rozkładu na elementy z ${\mathbb{\mathbb{N}}}_2\setminus ({\mathbb{\mathbb{N}}}_2+{\mathbb{\mathbb{N}}}_2)=\{2,3\}$.
Na przykład $6=2+2+2=3+3$.