PEE Moduł 14: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „<math> ” na „<math>” |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| Linia 10: | Linia 10: | ||
|valign="top"|'''Wprowadzenie''' | |valign="top"|'''Wprowadzenie''' | ||
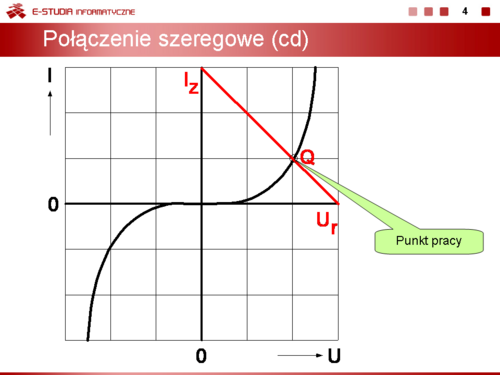
Mając do dyspozycji charakterystyki elementu nieliniowego można wykonać graficzną analizę obwodu zawierającego ten element. Przy połączeniu szeregowym przedstawionym na slajdzie suma napięć na elementach jest stała i równa się <math>E\</math>,. | Mając do dyspozycji charakterystyki elementu nieliniowego można wykonać graficzną analizę obwodu zawierającego ten element. Przy połączeniu szeregowym przedstawionym na slajdzie suma napięć na elementach jest stała i równa się <math>E\ </math>,. | ||
<math>E=I_QR+U_Q</math> | <math>E=I_QR+U_Q</math> | ||
Prąd <math>I_Q\</math>, oraz napięcie <math>U_Q</math> określają współrzędne punktu pracy elementu nieliniowego na jego charakterystyce prądowo-napięciowej. | Prąd <math>I_Q\ </math>, oraz napięcie <math>U_Q</math> określają współrzędne punktu pracy elementu nieliniowego na jego charakterystyce prądowo-napięciowej. | ||
| Linia 77: | Linia 77: | ||
<math>u(\omega t)=\sqrt{2}\cdot U\cdot sin\omega t</math> | <math>u(\omega t)=\sqrt{2}\cdot U\cdot sin\omega t</math> | ||
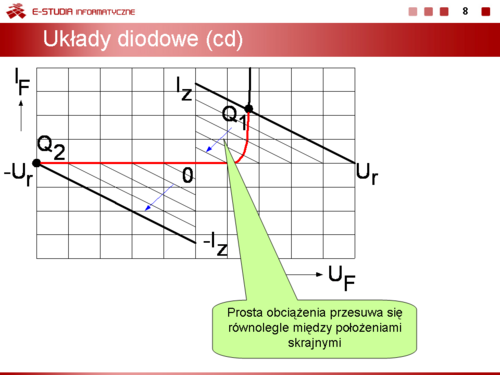
Przy takim sterowaniu dioda pracuje w dwóch stanach: stanie przewodzenia i stanie zaporowy. Punkt pracy przesuwa się po charakterystyce prądowo-napięciowej pomiędzy dwoma skrajnymi położeniami <math>Q_1\</math>, i <math>Q_2\</math>, | Przy takim sterowaniu dioda pracuje w dwóch stanach: stanie przewodzenia i stanie zaporowy. Punkt pracy przesuwa się po charakterystyce prądowo-napięciowej pomiędzy dwoma skrajnymi położeniami <math>Q_1\ </math>, i <math>Q_2\ </math>, | ||
|} | |} | ||
| Linia 84: | Linia 84: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M14_Slajd9.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M14_Slajd9.png|thumb|500px]] | ||
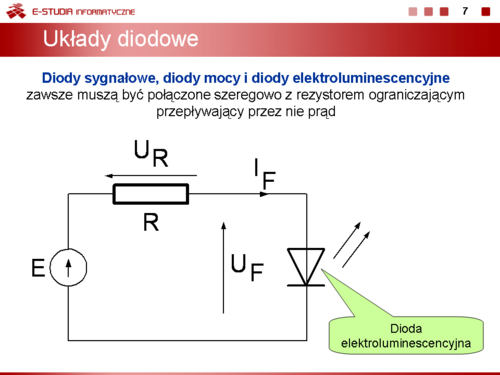
|valign="top"|Dla stabilistora (diody Zenera i diody lawinowej) obszarem roboczym jest najczęściej stan, w którym występuje polaryzacja zaporowa i przyrząd pracuje jak stabilizator napięcia (slajd 9). Z tego powodu, każdy stabilistor podobnie jak diody sygnałowe musi być dołączony do źródła zasilania przez rezystor. Rezystor musi ograniczyć wartość prądu w stabilistorze tak, aby nie została przekroczona graniczna wartość mocy strat. Na slajdzie przedstawiono zmianę położenia punktu pracy stabilistora pracującego w układzie parametrycznego stabilizatora napięcia przy zmianach wartości rezystancji szeregowej <math>R\</math>,. Istnieje pewna minimalna wartość rezystancji <math>R_{min}\</math>,, przekroczenie której spowoduje, że punktu pracy przesunie się powyżej krzywej dopuszczalnej mocy strat <math>P_{tot}\</math>, i stabilistor ulegnie uszkodzeniu. | |valign="top"|Dla stabilistora (diody Zenera i diody lawinowej) obszarem roboczym jest najczęściej stan, w którym występuje polaryzacja zaporowa i przyrząd pracuje jak stabilizator napięcia (slajd 9). Z tego powodu, każdy stabilistor podobnie jak diody sygnałowe musi być dołączony do źródła zasilania przez rezystor. Rezystor musi ograniczyć wartość prądu w stabilistorze tak, aby nie została przekroczona graniczna wartość mocy strat. Na slajdzie przedstawiono zmianę położenia punktu pracy stabilistora pracującego w układzie parametrycznego stabilizatora napięcia przy zmianach wartości rezystancji szeregowej <math>R\ </math>,. Istnieje pewna minimalna wartość rezystancji <math>R_{min}\ </math>,, przekroczenie której spowoduje, że punktu pracy przesunie się powyżej krzywej dopuszczalnej mocy strat <math>P_{tot}\ </math>, i stabilistor ulegnie uszkodzeniu. | ||
|} | |} | ||
| Linia 92: | Linia 92: | ||
|valign="top"|'''Układy tranzystorowe.''' | |valign="top"|'''Układy tranzystorowe.''' | ||
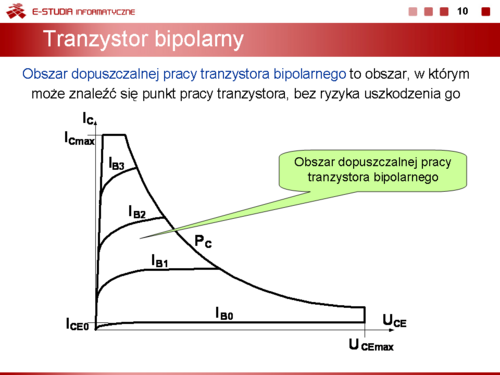
Obszar dopuszczalnej pracy tranzystora bipolarnego tzn. obszar w którym może znaleźć się punkt pracy tranzystora bez ryzyka jego szkodzenia można przedstawić posługując się charakterystykami wyjściowymi tranzystora. Obszar ten jest ograniczony krzywą mocy strat <math>P_C\</math>, lub <math>P_t_o_t\</math>,, która uwzględnia zjawisko powielania lawinowego nośników w złączu kolektorowym występujące przy dużych napięciach kolektor-emiter, wartością maksymalną prądu kolektora <math>I_C_m_a_x\</math>, , minimalnym prądem kolektora, który dla <math>I_B = 0\, A\</math>, jest równy prądowi zerowemu <math>I_C_E_0\</math>, oraz napięciem maksymalnym <math>U_C_E_m_a_x\</math>,. Minimalny prąd kolektora oraz napięcie maksymalne mogą być różne w zależności od sposobu sterownia tranzystora | Obszar dopuszczalnej pracy tranzystora bipolarnego tzn. obszar w którym może znaleźć się punkt pracy tranzystora bez ryzyka jego szkodzenia można przedstawić posługując się charakterystykami wyjściowymi tranzystora. Obszar ten jest ograniczony krzywą mocy strat <math>P_C\ </math>, lub <math>P_t_o_t\ </math>,, która uwzględnia zjawisko powielania lawinowego nośników w złączu kolektorowym występujące przy dużych napięciach kolektor-emiter, wartością maksymalną prądu kolektora <math>I_C_m_a_x\ </math>, , minimalnym prądem kolektora, który dla <math>I_B = 0\, A\ </math>, jest równy prądowi zerowemu <math>I_C_E_0\ </math>, oraz napięciem maksymalnym <math>U_C_E_m_a_x\ </math>,. Minimalny prąd kolektora oraz napięcie maksymalne mogą być różne w zależności od sposobu sterownia tranzystora | ||
|} | |} | ||
| Linia 99: | Linia 99: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M14_Slajd11.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M14_Slajd11.png|thumb|500px]] | ||
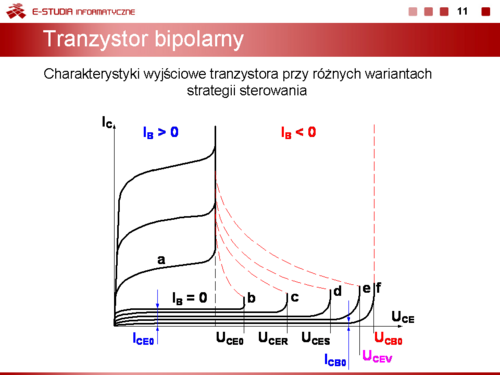
|valign="top"|Na slajdzie 11 przedstawiono charakterystyki wyjściowe tranzystora przy różnych wariantach strategii sterowania. Największą wartość napięcia kolektor-emiter <math>U_C_E_V\</math>,, zbliżoną do wartości <math>U_C_E_0\</math>, przy odłączonym emiterze można uzyskać, gdy baza jest wysterowana względem emitera ujemnym napięciem. | |valign="top"|Na slajdzie 11 przedstawiono charakterystyki wyjściowe tranzystora przy różnych wariantach strategii sterowania. Największą wartość napięcia kolektor-emiter <math>U_C_E_V\ </math>,, zbliżoną do wartości <math>U_C_E_0\ </math>, przy odłączonym emiterze można uzyskać, gdy baza jest wysterowana względem emitera ujemnym napięciem. | ||
|} | |} | ||
| Linia 111: | Linia 111: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M14_Slajd13.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M14_Slajd13.png|thumb|500px]] | ||
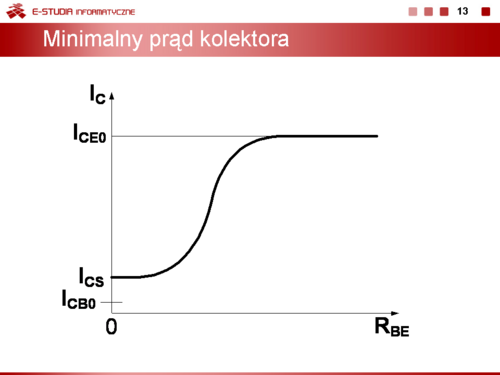
|valign="top"|W zależności od wartości rezystancji <math>R_B_E\</math>, dołączonej równolegle do złącza baza-emiter minimalny prąd kolektora będzie zmieniał się jak na wykresie przedstawionym na slajdzie 13. Prąd <math>I_C_S\</math>, odpowiada stanowi, gdy <math>I_B < 0\, A</math> i <math>R_B_E = 0\, \Omega</math> (przypadek przedstawiony na slajdzie 12, rys. e). | |valign="top"|W zależności od wartości rezystancji <math>R_B_E\ </math>, dołączonej równolegle do złącza baza-emiter minimalny prąd kolektora będzie zmieniał się jak na wykresie przedstawionym na slajdzie 13. Prąd <math>I_C_S\ </math>, odpowiada stanowi, gdy <math>I_B < 0\, A</math> i <math>R_B_E = 0\, \Omega</math> (przypadek przedstawiony na slajdzie 12, rys. e). | ||
|} | |} | ||
| Linia 119: | Linia 119: | ||
|valign="top"|'''Punkt pracy tranzystora bipolarnego''' | |valign="top"|'''Punkt pracy tranzystora bipolarnego''' | ||
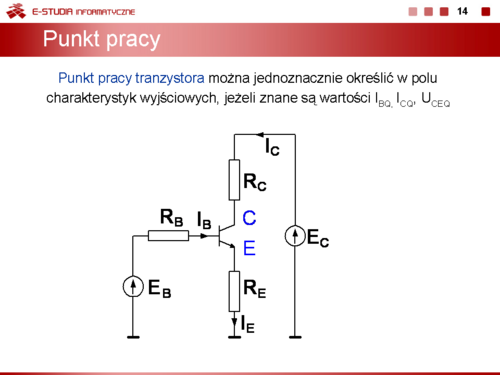
Punkt pracy tranzystora można jednoznacznie określić w polu charakterystyk wyjściowych, jeżeli znane są <math>I_B_Q,\, I_C_Q,\, U_C_E_Q\</math>, oraz rezystancje <math>R_B,\, R_C,\, R_E\</math>, i napięcia źródeł zasilania <math>E_B,\, E_C\</math>,. W rzeczywistości postępujemy na ogół inaczej: przyjmujemy parametry tranzystora w punkcie pracy i dla zadanych napięć źródeł zasilania dobieramy odpowiednie wartości rezystancji <math>R_B,\, R_C,\, R_E\</math>,. | Punkt pracy tranzystora można jednoznacznie określić w polu charakterystyk wyjściowych, jeżeli znane są <math>I_B_Q,\, I_C_Q,\, U_C_E_Q\ </math>, oraz rezystancje <math>R_B,\, R_C,\, R_E\ </math>, i napięcia źródeł zasilania <math>E_B,\, E_C\ </math>,. W rzeczywistości postępujemy na ogół inaczej: przyjmujemy parametry tranzystora w punkcie pracy i dla zadanych napięć źródeł zasilania dobieramy odpowiednie wartości rezystancji <math>R_B,\, R_C,\, R_E\ </math>,. | ||
|} | |} | ||
| Linia 129: | Linia 129: | ||
Przy zwarciu można napisać | Przy zwarciu można napisać | ||
<math>E_C-I_C_z\cdot R_C+I_E_z\cdot R_E</math> gdzie <math>I_C_z = \alpha_0\cdot I_E_z\</math>, | <math>E_C-I_C_z\cdot R_C+I_E_z\cdot R_E</math> gdzie <math>I_C_z = \alpha_0\cdot I_E_z\ </math>, | ||
Zatem | Zatem | ||
| Linia 149: | Linia 149: | ||
|width="500px" valign="top"|[[Grafika:PEE_M14_Slajd16.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M14_Slajd16.png|thumb|500px]] | ||
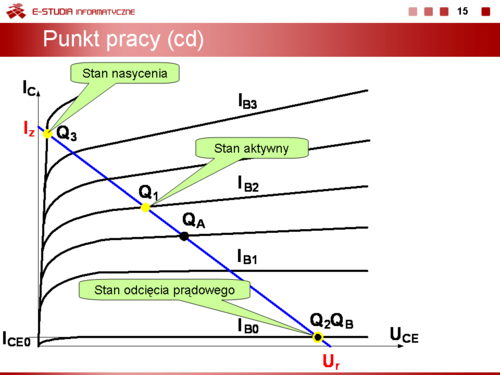
|valign="top"|W zależności od położenia punktu pracy w polu charakterystyk tranzystora wyróżnia się: | |valign="top"|W zależności od położenia punktu pracy w polu charakterystyk tranzystora wyróżnia się: | ||
*stan przewodzenia aktywnego, kiedy punkt pracy leży wewnątrz obszaru dopuszczalnej pracy (np. punkt <math>Q_1\</math>, na slajdzie 15). W tym stanie prąd kolektora i napięcie kolektor-emiter mają stosunkowo duże wartości. | *stan przewodzenia aktywnego, kiedy punkt pracy leży wewnątrz obszaru dopuszczalnej pracy (np. punkt <math>Q_1\ </math>, na slajdzie 15). W tym stanie prąd kolektora i napięcie kolektor-emiter mają stosunkowo duże wartości. | ||
*stan odcięcia prądowego, kiedy punkt pracy znajduje się na najniżej położonej charakterystyce (np. punkt <math>Q_2\</math>, na slajdzie15). W tym stanie tranzystor praktycznie nie przewodzi, prąd kolektora jest pomijalnie mały (np. równy <math>I_C_E_0</math>), a napięcie kolektor-emiter jest porównywalne lub równe napięciu zasilania. | *stan odcięcia prądowego, kiedy punkt pracy znajduje się na najniżej położonej charakterystyce (np. punkt <math>Q_2\ </math>, na slajdzie15). W tym stanie tranzystor praktycznie nie przewodzi, prąd kolektora jest pomijalnie mały (np. równy <math>I_C_E_0</math>), a napięcie kolektor-emiter jest porównywalne lub równe napięciu zasilania. | ||
*stan nasycenia prądowego, kiedy punkt pracy leży w obszarze nasycenia (na tzw. prostej nasycenia, np. punkt <math>Q_3\</math>, na slajdzie 15). W tym stanie tranzystor zachowuje się jak zamknięty łącznik, prąd kolektora jest duży, a napięcie kolektor-emiter jest praktycznie równe 0 V (pomijamy w tym wypadku napięcie nasycenia tranzystora <math>U_C_E_s\approx 0,2\, V</math>). | *stan nasycenia prądowego, kiedy punkt pracy leży w obszarze nasycenia (na tzw. prostej nasycenia, np. punkt <math>Q_3\ </math>, na slajdzie 15). W tym stanie tranzystor zachowuje się jak zamknięty łącznik, prąd kolektora jest duży, a napięcie kolektor-emiter jest praktycznie równe 0 V (pomijamy w tym wypadku napięcie nasycenia tranzystora <math>U_C_E_s\approx 0,2\, V</math>). | ||
|} | |} | ||
| Linia 171: | Linia 171: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M14_Slajd18.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M14_Slajd18.png|thumb|500px]] | ||
|valign="top"|''Współrzędne punktu pracy tranzystora bipolarnego'' <math>I_C_Q\</math> i <math>U_C_E_Q</math> zależą od parametrów obwodu zewnętrznego dołączonego do tranzystora (napięcie zasilania <math>U_C_C</math>, rezystory <math>R_C,\, R_E,\, R_B\</math>,) oraz od parametrów tranzystora. Przyjmuje się, z pośród wielu parametrów tranzystora trzy z nich: napięcie <math>U_B_E\</math>,, prąd <math>I_{CB0}\</math>,, współczynnik wzmocnienia prądowego <math>\alpha_0</math> lub <math>\beta_0</math> , są potrzebna do jednoznacznego określenia punktu pracy tranzystora. | |valign="top"|''Współrzędne punktu pracy tranzystora bipolarnego'' <math>I_C_Q\ </math> i <math>U_C_E_Q</math> zależą od parametrów obwodu zewnętrznego dołączonego do tranzystora (napięcie zasilania <math>U_C_C</math>, rezystory <math>R_C,\, R_E,\, R_B\ </math>,) oraz od parametrów tranzystora. Przyjmuje się, z pośród wielu parametrów tranzystora trzy z nich: napięcie <math>U_B_E\ </math>,, prąd <math>I_{CB0}\ </math>,, współczynnik wzmocnienia prądowego <math>\alpha_0</math> lub <math>\beta_0</math> , są potrzebna do jednoznacznego określenia punktu pracy tranzystora. | ||
Obwód przedstawiony na slajdzie 18 można opisać układem równań | Obwód przedstawiony na slajdzie 18 można opisać układem równań | ||
| Linia 233: | Linia 233: | ||
<math>S_{\beta}=\frac{dI_{CQ}}{d\beta_0}\bigg|_{\begin{matrix} U_{BE}=const \\ I_{CB0}=const \end{matrix}}</math> | <math>S_{\beta}=\frac{dI_{CQ}}{d\beta_0}\bigg|_{\begin{matrix} U_{BE}=const \\ I_{CB0}=const \end{matrix}}</math> | ||
Zagadnienia związane ze stabilizacją termiczną punktu pracy dotyczą wyłącznie składowych stałych prądów i napięć polaryzujących tranzystor bipolarny. A zatem na wartość współczynników stabilizacji nie wpływają wartości parametrów małosygnałowych (dynamicznych). Dla tranzystorów krzemowych istotniejszy jest współczynnik <math>S_u\</math>, a nie <math>S_i\</math>,. | Zagadnienia związane ze stabilizacją termiczną punktu pracy dotyczą wyłącznie składowych stałych prądów i napięć polaryzujących tranzystor bipolarny. A zatem na wartość współczynników stabilizacji nie wpływają wartości parametrów małosygnałowych (dynamicznych). Dla tranzystorów krzemowych istotniejszy jest współczynnik <math>S_u\ </math>, a nie <math>S_i\ </math>,. | ||
|} | |} | ||
| Linia 256: | Linia 256: | ||
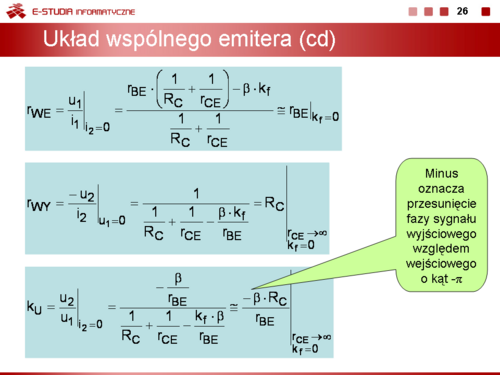
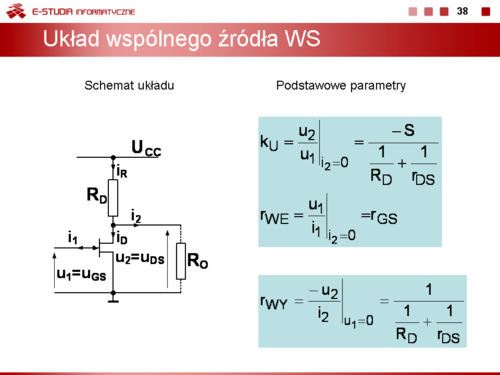
<math>k_{U}=\frac{u_2}{u_1}\bigg|_{i_2=0}</math> wzmocnienie napięciowe. | <math>k_{U}=\frac{u_2}{u_1}\bigg|_{i_2=0}</math> wzmocnienie napięciowe. | ||
Znak minus w definicji rezystancji wyjściowej wynika z przyjęcia, przeciwnego niż to jest przyjęte w teorii czwórników, zwrotu prądu <math>i_2\</math>, | Znak minus w definicji rezystancji wyjściowej wynika z przyjęcia, przeciwnego niż to jest przyjęte w teorii czwórników, zwrotu prądu <math>i_2\ </math>, | ||
Jeżeli, jak to często ma miejsce, prąd <math>i_2\</math>, wypływa ze wzmacniacza to w definicji rezystancji wyjściowej należy dopisać znak minus (w tym wypadku przyjęty kierunek prądu jest przeciwny do tego, który przyjęto w teorii czwórników). | Jeżeli, jak to często ma miejsce, prąd <math>i_2\ </math>, wypływa ze wzmacniacza to w definicji rezystancji wyjściowej należy dopisać znak minus (w tym wypadku przyjęty kierunek prądu jest przeciwny do tego, który przyjęto w teorii czwórników). | ||
|} | |} | ||
| Linia 264: | Linia 264: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M14_Slajd24.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M14_Slajd24.png|thumb|500px]] | ||
|valign="top"|Przy wyznaczaniu tych parametrów stosuje się małosygnałowy model tranzystora bipolarnego opisany równaniami macierzy hybrydowej <math>h\</math>, z parametrami w postaci uniwersalnej. | |valign="top"|Przy wyznaczaniu tych parametrów stosuje się małosygnałowy model tranzystora bipolarnego opisany równaniami macierzy hybrydowej <math>h\ </math>, z parametrami w postaci uniwersalnej. | ||
<math>u_{BE}=i_B\cdot r_{BE}+u_{CE}\cdot k_f</math> | <math>u_{BE}=i_B\cdot r_{BE}+u_{CE}\cdot k_f</math> | ||
| Linia 287: | Linia 287: | ||
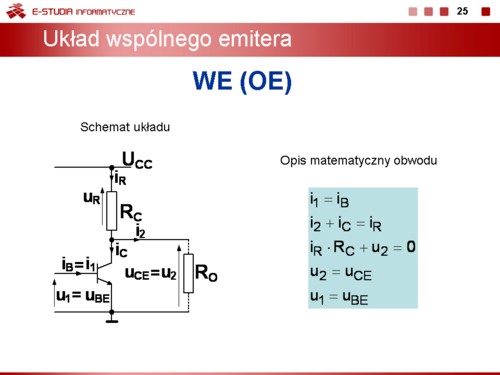
Warunek <math>i_R\cdot R_C + u_2 = 0</math> oznacza, że przyrosty napięć na rezystorze kolektorowym | Warunek <math>i_R\cdot R_C + u_2 = 0</math> oznacza, że przyrosty napięć na rezystorze kolektorowym | ||
i tranzystorze kompensują się. Wynika to z faktu, że napięcie zasilania <math>U_{CC}\</math>, jest stałe tzn. nie zmienia się w czasie | i tranzystorze kompensują się. Wynika to z faktu, że napięcie zasilania <math>U_{CC}\ </math>, jest stałe tzn. nie zmienia się w czasie | ||
|} | |} | ||
| Linia 301: | Linia 301: | ||
<math>-\frac{u_2}{R_C}=i_1\cdot \beta +u_2\cdot \frac{1}{r_{CE}}</math> | <math>-\frac{u_2}{R_C}=i_1\cdot \beta +u_2\cdot \frac{1}{r_{CE}}</math> | ||
Rugując z tego układu równań prąd <math>i_1\</math>, wzmocnienie napięciowe jest opisane zależnością | Rugując z tego układu równań prąd <math>i_1\ </math>, wzmocnienie napięciowe jest opisane zależnością | ||
<math>k_U=\frac{u_2}{u_1}\bigg|_{i_2=0} =\frac{-\frac{\beta}{r_{BE}}}{\frac{1}{R_C}+\frac{1}{r_{CE}}-\frac{k_f\cdot \beta}{r_{BE}}}\cong \frac{-\beta\cdot R_C}{r_{BE}}\bigg|_{\begin{matrix} r_{CE}\to \infty \\ k_f=0 \end{matrix}}</math> | <math>k_U=\frac{u_2}{u_1}\bigg|_{i_2=0} =\frac{-\frac{\beta}{r_{BE}}}{\frac{1}{R_C}+\frac{1}{r_{CE}}-\frac{k_f\cdot \beta}{r_{BE}}}\cong \frac{-\beta\cdot R_C}{r_{BE}}\bigg|_{\begin{matrix} r_{CE}\to \infty \\ k_f=0 \end{matrix}}</math> | ||
| Linia 320: | Linia 320: | ||
<math>-\frac{u_2}{R_C}-i_2=i_1\cdot \beta +u_2\cdot \frac{1}{r_{CE}}</math> | <math>-\frac{u_2}{R_C}-i_2=i_1\cdot \beta +u_2\cdot \frac{1}{r_{CE}}</math> | ||
Rugując z tego układu równań napięcie <math>u_2\</math>, rezystancja wyjściowa jest opisane zależnością | Rugując z tego układu równań napięcie <math>u_2\ </math>, rezystancja wyjściowa jest opisane zależnością | ||
<math>r_{WY}=\frac{-u_2}{i_2}\bigg|_{u_1=0} =\frac{1}{\frac{1}{R_C}+\frac{1}{r_{CE}}-\frac{\beta\cdot k_f}{r_{BE}}}= R_C \bigg|_{\begin{matrix} r_{CE}\to \infty \\ k_f=0 \end{matrix}}</math> | <math>r_{WY}=\frac{-u_2}{i_2}\bigg|_{u_1=0} =\frac{1}{\frac{1}{R_C}+\frac{1}{r_{CE}}-\frac{\beta\cdot k_f}{r_{BE}}}= R_C \bigg|_{\begin{matrix} r_{CE}\to \infty \\ k_f=0 \end{matrix}}</math> | ||
| Linia 402: | Linia 402: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M14_Slajd31.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M14_Slajd31.png|thumb|500px]] | ||
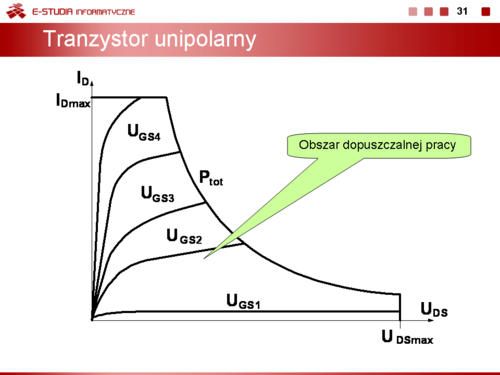
|valign="top"|''Obszar dopuszczalnej pracy tranzystora unipolarnego'' tzn. obszar w którym może znaleźć się punkt pracy tranzystora bez ryzyka jego szkodzenia można, podobnie jak dla tranzystorów bipolarnych, można przedstawić posługując się charakterystykami wyjściowymi tranzystora. Obszar ten jest ograniczony krzywą mocy strat <math>P_{tot}\</math>,, wartością maksymalną prądu drenu <math>I_{Dmax}\</math>, , oraz napięciem maksymalnym <math>U_{DSmax}\</math>,. | |valign="top"|''Obszar dopuszczalnej pracy tranzystora unipolarnego'' tzn. obszar w którym może znaleźć się punkt pracy tranzystora bez ryzyka jego szkodzenia można, podobnie jak dla tranzystorów bipolarnych, można przedstawić posługując się charakterystykami wyjściowymi tranzystora. Obszar ten jest ograniczony krzywą mocy strat <math>P_{tot}\ </math>,, wartością maksymalną prądu drenu <math>I_{Dmax}\ </math>, , oraz napięciem maksymalnym <math>U_{DSmax}\ </math>,. | ||
|} | |} | ||
| Linia 411: | Linia 411: | ||
|valign="top"|'''Punkt pracy tranzystora unipolarnego''' | |valign="top"|'''Punkt pracy tranzystora unipolarnego''' | ||
Punkt pracy tranzystora można jednoznacznie określić w polu charakterystyk wyjściowych, jeżeli znane są <math>U_{GSQ},\, I_{DQ},\, U_{DSQ}\</math>,. Załóżmy, że dane są charakterystyki wyjściowe tranzystora pracującego w układzie wzmacniacza przedstawionego na slajdzie 32. Postępując podobnie jak w układach z tranzystorami bipolarnymi możemy oddzielić część liniową obwodu od części nieliniowej. Część nieliniowa (tranzystor) ma znaną charakterystykę prądowo-napięciową. Charakterystyka części liniowej obwodu jest liniowa. Dwa punktu tej charakterystyki określamy zwierając i rozwierając elektrody D i S tranzystora. | Punkt pracy tranzystora można jednoznacznie określić w polu charakterystyk wyjściowych, jeżeli znane są <math>U_{GSQ},\, I_{DQ},\, U_{DSQ}\ </math>,. Załóżmy, że dane są charakterystyki wyjściowe tranzystora pracującego w układzie wzmacniacza przedstawionego na slajdzie 32. Postępując podobnie jak w układach z tranzystorami bipolarnymi możemy oddzielić część liniową obwodu od części nieliniowej. Część nieliniowa (tranzystor) ma znaną charakterystykę prądowo-napięciową. Charakterystyka części liniowej obwodu jest liniowa. Dwa punktu tej charakterystyki określamy zwierając i rozwierając elektrody D i S tranzystora. | ||
Ponieważ <math>E_D=I_{Dz}\cdot (R_D+R_S)</math> | Ponieważ <math>E_D=I_{Dz}\cdot (R_D+R_S)</math> | ||
| Linia 425: | Linia 425: | ||
<math>I_r=0\,A,\, U_r=E_D</math> | <math>I_r=0\,A,\, U_r=E_D</math> | ||
Punkt przecięcia tak wyznaczonej prostej (tzw. prostej obciążenia) z charakterystyką tranzystora odpowiadającą napięciu <math>U_{GS}\</math>,, które w tym wypadku będzie również równe napięciu <math>U_{GSQ}\</math>, wyznaczy współrzędne punktu pracy</math>I_{DQ}\</math>, oraz <math>U_{DSQ}\</math>, wyznaczy współrzędne punktu pracy <math>I_{DQ}\</math>, oraz <math>U_{DSQ}\</math>,. | Punkt przecięcia tak wyznaczonej prostej (tzw. prostej obciążenia) z charakterystyką tranzystora odpowiadającą napięciu <math>U_{GS}\ </math>,, które w tym wypadku będzie również równe napięciu <math>U_{GSQ}\ </math>, wyznaczy współrzędne punktu pracy</math>I_{DQ}\ </math>, oraz <math>U_{DSQ}\ </math>, wyznaczy współrzędne punktu pracy <math>I_{DQ}\ </math>, oraz <math>U_{DSQ}\ </math>,. | ||
|} | |} | ||
| Linia 434: | Linia 434: | ||
|valign="top"|W zależności od położenia punktu pracy w polu charakterystyk tranzystora wyróżnia się: | |valign="top"|W zależności od położenia punktu pracy w polu charakterystyk tranzystora wyróżnia się: | ||
*stan aktywny, kiedy punkt pracy leży wewnątrz obszaru dopuszczalnej pracy (np. punkt <math>Q_1\</math>, na slajdzie 32). W tym stanie tranzystor jest wzmacniaczem, prąd drenu i napięcie dren-źródło mają stosunkowo duże wartości. | *stan aktywny, kiedy punkt pracy leży wewnątrz obszaru dopuszczalnej pracy (np. punkt <math>Q_1\ </math>, na slajdzie 32). W tym stanie tranzystor jest wzmacniaczem, prąd drenu i napięcie dren-źródło mają stosunkowo duże wartości. | ||
*stan wyłączenia, kiedy punkt pracy jest położony najniżej na prostej obciążenia (punkt <math>Q_2\</math>, na slajdzie 32). W tym stanie tranzystor praktycznie nie przewodzi, prąd drenu jest pomijalnie mały, a napięcie dren-źródło jest porównywalne lub równe napięciu zasilania. | *stan wyłączenia, kiedy punkt pracy jest położony najniżej na prostej obciążenia (punkt <math>Q_2\ </math>, na slajdzie 32). W tym stanie tranzystor praktycznie nie przewodzi, prąd drenu jest pomijalnie mały, a napięcie dren-źródło jest porównywalne lub równe napięciu zasilania. | ||
*stan załączenia, kiedy punkt pracy leży w obszarze pracy triodowej (np. punkt <math>Q_3\</math>, na slajdzie 32). W tym stanie tranzystor zachowuje się jak zamknięty łącznik, o stosunkowo małej rezystancji, prąd drenu jest duży, a napięcie dren-źródło jest małe. | *stan załączenia, kiedy punkt pracy leży w obszarze pracy triodowej (np. punkt <math>Q_3\ </math>, na slajdzie 32). W tym stanie tranzystor zachowuje się jak zamknięty łącznik, o stosunkowo małej rezystancji, prąd drenu jest duży, a napięcie dren-źródło jest małe. | ||
|} | |} | ||
| Linia 445: | Linia 445: | ||
|valign="top"|Podobnie jak w wypadku tranzystorów bipolarnych w zależności od położenia punktu pracy na prostej obciążenia wyróżnia się tzw. klasy pracy układu. | |valign="top"|Podobnie jak w wypadku tranzystorów bipolarnych w zależności od położenia punktu pracy na prostej obciążenia wyróżnia się tzw. klasy pracy układu. | ||
Jeżeli punkt pracy leży w środku prostej obciążenia mówimy, że wzmacniacz pracuje w klasie A, punkt <math>Q_A\</math>, na slajdzie 32. | Jeżeli punkt pracy leży w środku prostej obciążenia mówimy, że wzmacniacz pracuje w klasie A, punkt <math>Q_A\ </math>, na slajdzie 32. | ||
Jeżeli punkt pracy leży na charakterystyce w punkcie <math>Q_B\</math>, mówimy, że wzmacniacz pracuje w klasie B. | Jeżeli punkt pracy leży na charakterystyce w punkcie <math>Q_B\ </math>, mówimy, że wzmacniacz pracuje w klasie B. | ||
Jeżeli punkt pracy <math>Q_{AB}\</math>, leży pomiędzy punktami <math>Q_A\</math>, i <math>Q_B\</math>, mówimy, że wzmacniacz pracuje w klasie AB. | Jeżeli punkt pracy <math>Q_{AB}\ </math>, leży pomiędzy punktami <math>Q_A\ </math>, i <math>Q_B\ </math>, mówimy, że wzmacniacz pracuje w klasie AB. | ||
W praktyce stosuje się także inne klasy pracy wzmacniacza np. klasy C, D, E. | W praktyce stosuje się także inne klasy pracy wzmacniacza np. klasy C, D, E. | ||
| Linia 460: | Linia 460: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M14_Slajd35.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M14_Slajd35.png|thumb|500px]] | ||
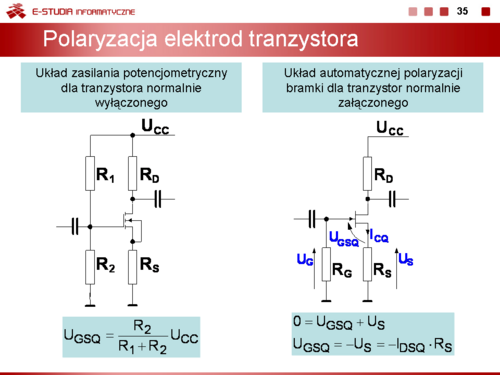
|valign="top"|''Współrzędne punktu pracy tranzystora unipolarnego'' <math>I_{DQ}\</math>, i <math>U_{DSQ}\</math>, zależą od parametrów obwodu zewnętrznego dołączonego do tranzystora (napięcie zasilania <math>U_{CC}\</math>,, rezystory <math>R_D\</math>,, <math>R_S\</math>,) oraz od parametrów tranzystora. | |valign="top"|''Współrzędne punktu pracy tranzystora unipolarnego'' <math>I_{DQ}\ </math>, i <math>U_{DSQ}\ </math>, zależą od parametrów obwodu zewnętrznego dołączonego do tranzystora (napięcie zasilania <math>U_{CC}\ </math>,, rezystory <math>R_D\ </math>,, <math>R_S\ </math>,) oraz od parametrów tranzystora. | ||
Dla tranzystorów unipolarnych zagadnienie polaryzacji i stabilizacji punktu pracy jest znacznie prostsze niż w wypadku tranzystorów bipolarnych ponieważ charakterystyki w mniejszym stopniu są zależne od temperatury, a ponieważ współczynniki termiczne są ujemne to niekorzystne skutki tych zjawisk często kompensują się. Ponadto w tranzystorze unipolarnym praktycznie nie płynie prąd bramki. W zasadzie istnieją dwa układy zasilania tranzystorów unipolarnych. Pierwszy potencjometryczny stosowany w wypadku tranzystorów normalnie wyłączonych i drugi z tzw. automatyczna polaryzacją bramki stosowany do tranzystorów normalnie załączonych. | Dla tranzystorów unipolarnych zagadnienie polaryzacji i stabilizacji punktu pracy jest znacznie prostsze niż w wypadku tranzystorów bipolarnych ponieważ charakterystyki w mniejszym stopniu są zależne od temperatury, a ponieważ współczynniki termiczne są ujemne to niekorzystne skutki tych zjawisk często kompensują się. Ponadto w tranzystorze unipolarnym praktycznie nie płynie prąd bramki. W zasadzie istnieją dwa układy zasilania tranzystorów unipolarnych. Pierwszy potencjometryczny stosowany w wypadku tranzystorów normalnie wyłączonych i drugi z tzw. automatyczna polaryzacją bramki stosowany do tranzystorów normalnie załączonych. | ||
| Linia 474: | Linia 474: | ||
<math>U_S=I_{DSQ}\cdot R_S</math> | <math>U_S=I_{DSQ}\cdot R_S</math> | ||
Prąd <math>I_{DSQ}\</math>, jest równy prądowi drenu w wybranym punkcie pracy dla <math>U_{GS} = U_{GSQ}</math>. Ponieważ prąd bramki w tranzystorze unipolarnym praktycznie nie płynie <math>(I_G = 0\, A)</math> to nawet kiedy rezystancja <math>R_G\</math>, będzie bardzo wielka (np. rzędu <math>1\, M\Omega\</math>,) spadek napięcia na niej także będzie równy <math>U_G = 0\, V</math>. | Prąd <math>I_{DSQ}\ </math>, jest równy prądowi drenu w wybranym punkcie pracy dla <math>U_{GS} = U_{GSQ}</math>. Ponieważ prąd bramki w tranzystorze unipolarnym praktycznie nie płynie <math>(I_G = 0\, A)</math> to nawet kiedy rezystancja <math>R_G\ </math>, będzie bardzo wielka (np. rzędu <math>1\, M\Omega\ </math>,) spadek napięcia na niej także będzie równy <math>U_G = 0\, V</math>. | ||
Otrzymamy zatem następujące zależności | Otrzymamy zatem następujące zależności | ||
| Linia 509: | Linia 509: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M14_Slajd37.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M14_Slajd37.png|thumb|500px]] | ||
|valign="top"|Przy wyznaczaniu tych parametrów można wykorzystać małosygnałowy model tranzystora unipolarnego opisany równaniami macierzy admitancyjnej <math>y\</math>, | |valign="top"|Przy wyznaczaniu tych parametrów można wykorzystać małosygnałowy model tranzystora unipolarnego opisany równaniami macierzy admitancyjnej <math>y\ </math>, | ||
z parametrami w postaci uniwersalnej. | z parametrami w postaci uniwersalnej. | ||
| Linia 572: | Linia 572: | ||
<math>\frac{u_2}{R_S}=S\cdot (u_1-u_2)-\frac{u_2}{r_{DS}}</math> | <math>\frac{u_2}{R_S}=S\cdot (u_1-u_2)-\frac{u_2}{r_{DS}}</math> | ||
Po przekształceniu tej zależności wzmocnienie napięciowe <math>k_U\</math>, układu wspólnego źródła jest równe | Po przekształceniu tej zależności wzmocnienie napięciowe <math>k_U\ </math>, układu wspólnego źródła jest równe | ||
<math>k_U=\frac{S}{S+\frac{1}{R_S}+\frac{1}{r_{DS}}}\cong 1\frac{V}{V}</math> | <math>k_U=\frac{S}{S+\frac{1}{R_S}+\frac{1}{r_{DS}}}\cong 1\frac{V}{V}</math> | ||
Warto zauważyć, że <math>k_U\</math>, ma zawsze wartość mniejszą od 1. | Warto zauważyć, że <math>k_U\ </math>, ma zawsze wartość mniejszą od 1. | ||
Rezystancja wejściowa po uwzględnieniu zależności <math>u_1-u_2=i_1\cdot r_{GS}</math> jest równa | Rezystancja wejściowa po uwzględnieniu zależności <math>u_1-u_2=i_1\cdot r_{GS}</math> jest równa | ||
Aktualna wersja na dzień 12:05, 5 wrz 2023
 |
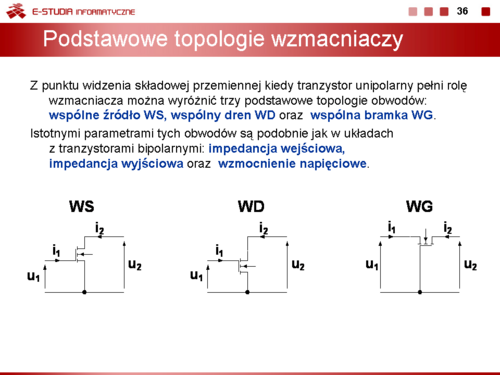
Podstawowe topologie połączeń elementów półprzewodnikowych: punkt pracy, stany pracy
|
 |
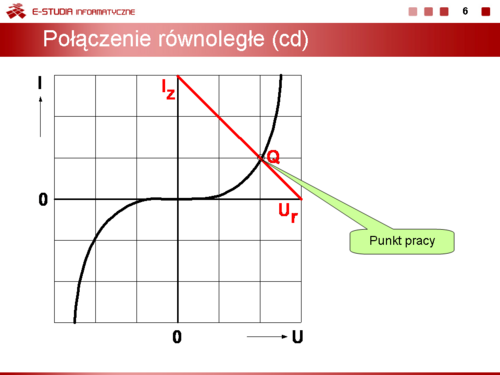
Przy połączeniu równoległym suma prądów jest stała i równa I.
Podobnie jak przy połączeniu szeregowym prąd IQ oraz napięcie UQ określają współrzędne punktu pracy elementu nieliniowego. |
 |
Warianty sterowania |
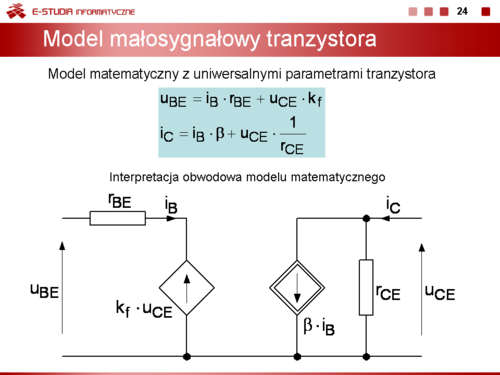 |
Przy wyznaczaniu tych parametrów stosuje się małosygnałowy model tranzystora bipolarnego opisany równaniami macierzy hybrydowej , z parametrami w postaci uniwersalnej.
|
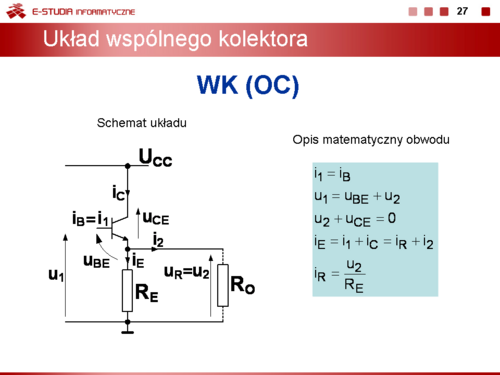 |
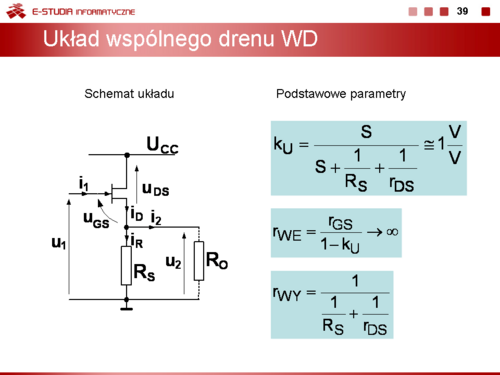
Dla układu wspólnego kolektora WK, często nazywanego także wtórnikiem emiterowym można zapisać
|
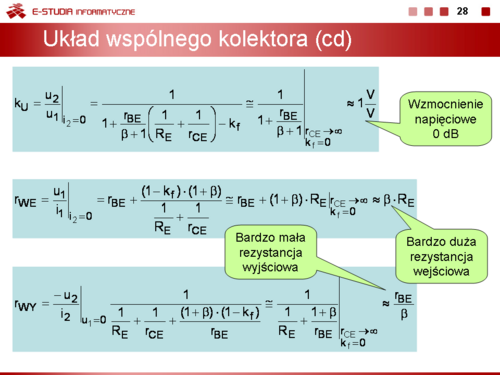 |
Wzmocnienie napięciowe tego układu jest bliskie, ale zawsze mniejsze od jedności
Rezystancja wejściowa jest równa
a rezystancja wyjściowa
|
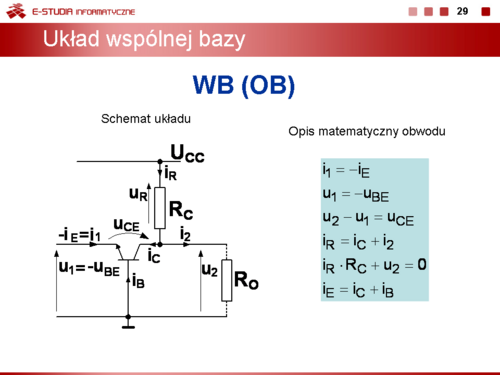 |
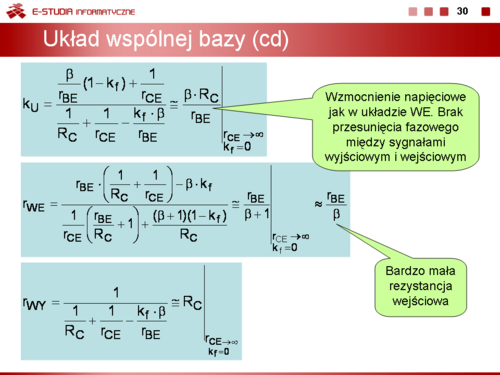
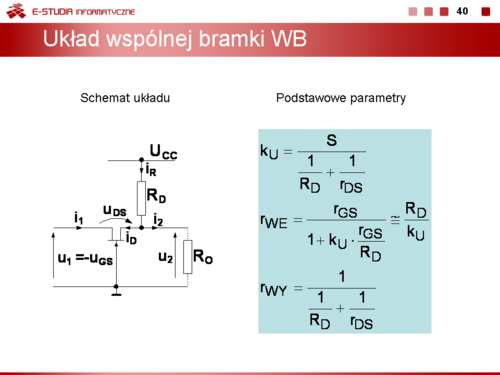
Dla układu wspólnej bazy WB można zapisać:
|
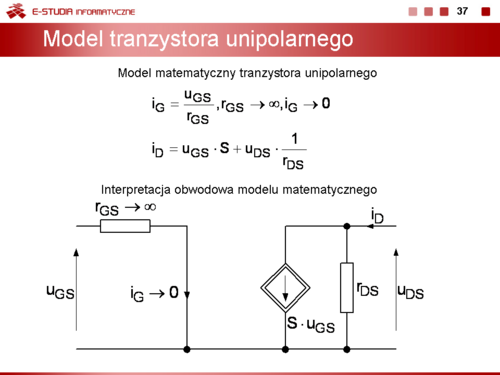 |
Przy wyznaczaniu tych parametrów można wykorzystać małosygnałowy model tranzystora unipolarnego opisany równaniami macierzy admitancyjnej ,
z parametrami w postaci uniwersalnej.
|
Bibliografia
- Kaźmierkowski M. P., Matysik J. T.: Wprowadzenie do elektroniki i energoelektroniki, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa 2005
- Baranowski J., Nosal Z.: Układy elektroniczne cz. I. Układy analogowe liniowe, Wydawnictwa Naukowo-Techniczne, Warszawa 1998