CWGI Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „ \</math>” na „</math>” |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| Linia 10: | Linia 10: | ||
|valign="top"|Celem naszym będzie poszukiwanie rzutów punków przebicia prostej z wielościanem. | |valign="top"|Celem naszym będzie poszukiwanie rzutów punków przebicia prostej z wielościanem. | ||
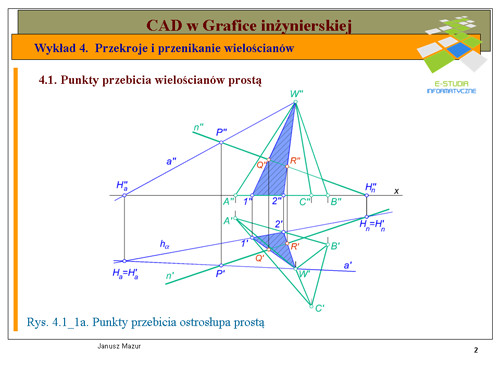
Niech będą dane rzuty ostrosłupa prostego stojącego na rzutni poziomej <math>ABCW</math> oraz rzuty prostej <math>n\</math>,. Należy wyznaczyć punkty przebicia prostej ze ścianami ostrosłupa oraz ustalić widoczność prostej przy założeniu, że ściany ostrosłupa są niewidoczne (patrz ''rys.4.1_1a''). | Niech będą dane rzuty ostrosłupa prostego stojącego na rzutni poziomej <math>ABCW</math> oraz rzuty prostej <math>n\ </math>,. Należy wyznaczyć punkty przebicia prostej ze ścianami ostrosłupa oraz ustalić widoczność prostej przy założeniu, że ściany ostrosłupa są niewidoczne (patrz ''rys.4.1_1a''). | ||
Ustalmy tok postępowania przy rozwiązaniu tego zadania: | Ustalmy tok postępowania przy rozwiązaniu tego zadania: | ||
#przez dowolny punkt <math>P\</math>, leżący na prostej <math>n\</math>, oraz wierzchołek <math>W\</math>, ostrosłupa poprowadźmy prostą <math>a\</math>,, | #przez dowolny punkt <math>P\ </math>, leżący na prostej <math>n\ </math>, oraz wierzchołek <math>W\ </math>, ostrosłupa poprowadźmy prostą <math>a\ </math>,, | ||
#dwie proste <math>a\</math>, i <math>n\</math>, wyznaczą płaszczyznę <math>\alpha\</math>,. Wyznaczamy przekrój ostrosłupa płaszczyzną <math>\alpha\</math>,, w której leży dana prosta <math>n\</math>, | #dwie proste <math>a\ </math>, i <math>n\ </math>, wyznaczą płaszczyznę <math>\alpha\ </math>,. Wyznaczamy przekrój ostrosłupa płaszczyzną <math>\alpha\ </math>,, w której leży dana prosta <math>n\ </math>, | ||
#w punktach przecięcia się boków wielokąta przekroju z prostą <math>n\</math>, wyznaczymy poszukiwane punkty przebicia ścian ostrosłupa z prostą <math>n\</math>,. | #w punktach przecięcia się boków wielokąta przekroju z prostą <math>n\ </math>, wyznaczymy poszukiwane punkty przebicia ścian ostrosłupa z prostą <math>n\ </math>,. | ||
Obierając punkt <math>P\</math>, na prostej <math>n\</math>, oraz prowadząc prostą a przez punkt <math>P\</math>, i wierzchołek <math>W\</math>, ostrosłupa wyznaczamy przekrój ostrosłupa płaszczyzną określoną przez te proste. Wierzchołek <math>W\</math>, będzie stanowił jeden z wierzchołków figury płaskiej, będącej poszukiwanym przekrojem. Mając dane rzuty prostych <math>n\</math>, i <math>a\</math>, możemy wyznaczyć ich ślady poziome <math>H_a</math> i <math>H_n</math>. Łącząc ze sobą te ślady wyznaczymy ślad poziomy <math>h_\alpha</math> płaszczyzny <math>\alpha\</math>,. Jak widać na rzucie poziomym ślad <math>h_\alpha</math> (prosta leżąca na rzutni poziomej) przecina nam podstawę ostrosłupa w punktach <math>1'\</math>, i <math>2'\</math>, (podstawa ostrosłupa z założenia leży na rzutni poziomej). Łącząc rzuty poziome punktów <math>1'\</math>, i <math>2'\</math>, z rzutem poziomym <math>W'\</math>, wierzchołka, wyznaczymy rzut poziomy (<math>W'1'2'</math>) trójkąta, który jest rzutem poszukiwanego przekroju. Prosta <math>n\</math>, przecina boki przekroju w punktach <math>Q'\</math>, i <math>R'\</math>,, które są punktami przebicia prostej <math>n\</math>, ze ścianami <math>\alpha\</math>, ostrosłupa. Rzuty pionowe punktów przebicia znajdziemy na rzucie pionowym <math>n"</math> prostej oraz odnoszących punktów <math>Q'\</math>, i <math>R'\</math>,. | Obierając punkt <math>P\ </math>, na prostej <math>n\ </math>, oraz prowadząc prostą a przez punkt <math>P\ </math>, i wierzchołek <math>W\ </math>, ostrosłupa wyznaczamy przekrój ostrosłupa płaszczyzną określoną przez te proste. Wierzchołek <math>W\ </math>, będzie stanowił jeden z wierzchołków figury płaskiej, będącej poszukiwanym przekrojem. Mając dane rzuty prostych <math>n\ </math>, i <math>a\ </math>, możemy wyznaczyć ich ślady poziome <math>H_a</math> i <math>H_n</math>. Łącząc ze sobą te ślady wyznaczymy ślad poziomy <math>h_\alpha</math> płaszczyzny <math>\alpha\ </math>,. Jak widać na rzucie poziomym ślad <math>h_\alpha</math> (prosta leżąca na rzutni poziomej) przecina nam podstawę ostrosłupa w punktach <math>1'\ </math>, i <math>2'\ </math>, (podstawa ostrosłupa z założenia leży na rzutni poziomej). Łącząc rzuty poziome punktów <math>1'\ </math>, i <math>2'\ </math>, z rzutem poziomym <math>W'\ </math>, wierzchołka, wyznaczymy rzut poziomy (<math>W'1'2'</math>) trójkąta, który jest rzutem poszukiwanego przekroju. Prosta <math>n\ </math>, przecina boki przekroju w punktach <math>Q'\ </math>, i <math>R'\ </math>,, które są punktami przebicia prostej <math>n\ </math>, ze ścianami <math>\alpha\ </math>, ostrosłupa. Rzuty pionowe punktów przebicia znajdziemy na rzucie pionowym <math>n"</math> prostej oraz odnoszących punktów <math>Q'\ </math>, i <math>R'\ </math>,. | ||
Ustalamy widoczność prostej <math>n\</math>,, przyjmując, że ściany ostrosłupa są nieprzezroczyste. Widoczność prostej <math>n\</math>, w rzucie pionowym określamy analizując widoczność ścian ostrosłupa (ocenę przeprowadzamy w rzucie poziomym). Widać wyraźnie, że ściana <math>ACW</math> jest widoczna w rzucie pionowym, natomiast ściana <math>ABW</math> jest niewidoczna w rzucie pionowym. Zaznaczamy to odpowiednio linią kreskową. Widoczność prostej <math>n\</math>, w rzucie poziomym jest oczywista. Wszystkie ściany są widoczne z wyjątkiem podstawy. Prosta <math>n\</math>,, zatem jest niewidoczna wyłącznie między ścianami ostrosłupa, co odpowiednio zaznaczamy na rzucie poziomym przekroju. | Ustalamy widoczność prostej <math>n\ </math>,, przyjmując, że ściany ostrosłupa są nieprzezroczyste. Widoczność prostej <math>n\ </math>, w rzucie pionowym określamy analizując widoczność ścian ostrosłupa (ocenę przeprowadzamy w rzucie poziomym). Widać wyraźnie, że ściana <math>ACW</math> jest widoczna w rzucie pionowym, natomiast ściana <math>ABW</math> jest niewidoczna w rzucie pionowym. Zaznaczamy to odpowiednio linią kreskową. Widoczność prostej <math>n\ </math>, w rzucie poziomym jest oczywista. Wszystkie ściany są widoczne z wyjątkiem podstawy. Prosta <math>n\ </math>,, zatem jest niewidoczna wyłącznie między ścianami ostrosłupa, co odpowiednio zaznaczamy na rzucie poziomym przekroju. | ||
|} | |} | ||
| Linia 28: | Linia 28: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M4_Slajd3.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M4_Slajd3.png]] | ||
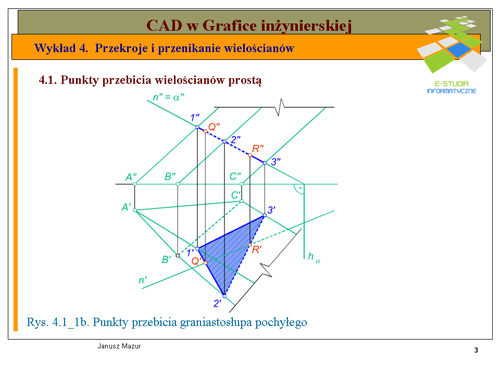
|valign="top"|Kolejnym zadaniem będzie poszukiwanie punktów przebicia prostej <math>n\</math>, ze ścianami graniastosłupa pochyłego <math>ABC</math> stojącego na rzutni poziomej. | |valign="top"|Kolejnym zadaniem będzie poszukiwanie punktów przebicia prostej <math>n\ </math>, ze ścianami graniastosłupa pochyłego <math>ABC</math> stojącego na rzutni poziomej. | ||
Pierwszym etapem rozwiązania zadania jest wyznaczenie rzutów przekroju graniastosłupa płaszczyzn, w której znajduje się dana prosta <math>n\</math>,. W tym celu przez prostą <math>n\</math>, prowadzimy dowolna płaszczyznę. Dla ułatwienia będzie to płaszczyzna pionowo – rzutująca <math>\alpha\</math>,, prostopadła do rzutni pionowej. Ślad pionowy płaszczyzny <math>v_\alpha</math> będzie pokrywał się z rzutem pionowym prostej <math>n\</math>,, ponieważ wszystkie elementy płaskie znajdujące się w takiej płaszczyźnie w rzucie pionowym rzutują się na ślad pionowy płaszczyzny, będący jednocześnie rzutem pionowym płaszczyzny. Kolejnym etapem rozwiązania jest wyznaczenie przekroju graniastosłupa płaszczyzną <math>\alpha\</math>,. Przekrój w rzucie pionowym wyznaczymy natychmiast. Zgodnie z cytowaną wyżej zasadą punkty przekroju <math>1", 2", 3"</math> w rzucie pionowym będą leżały na przecięciu się krawędzi graniastosłupa <math>A",B", C"</math> ze śladem pionowym płaszczyzny <math>\alpha\</math>,. Rzuty poziome punktów przekroju <math>1', 2', 3'</math> będą leżały na przecięciu się odnoszących z rzutami poziomymi krawędzi graniastosłupa <math>A', B', C'</math>. W miejscach gdzie prosta n przecina się z bokami przekroju otrzymamy poszukiwane punkty przebicia graniastosłupa prostą <math>n\</math>,. | Pierwszym etapem rozwiązania zadania jest wyznaczenie rzutów przekroju graniastosłupa płaszczyzn, w której znajduje się dana prosta <math>n\ </math>,. W tym celu przez prostą <math>n\ </math>, prowadzimy dowolna płaszczyznę. Dla ułatwienia będzie to płaszczyzna pionowo – rzutująca <math>\alpha\ </math>,, prostopadła do rzutni pionowej. Ślad pionowy płaszczyzny <math>v_\alpha</math> będzie pokrywał się z rzutem pionowym prostej <math>n\ </math>,, ponieważ wszystkie elementy płaskie znajdujące się w takiej płaszczyźnie w rzucie pionowym rzutują się na ślad pionowy płaszczyzny, będący jednocześnie rzutem pionowym płaszczyzny. Kolejnym etapem rozwiązania jest wyznaczenie przekroju graniastosłupa płaszczyzną <math>\alpha\ </math>,. Przekrój w rzucie pionowym wyznaczymy natychmiast. Zgodnie z cytowaną wyżej zasadą punkty przekroju <math>1", 2", 3"</math> w rzucie pionowym będą leżały na przecięciu się krawędzi graniastosłupa <math>A",B", C"</math> ze śladem pionowym płaszczyzny <math>\alpha\ </math>,. Rzuty poziome punktów przekroju <math>1', 2', 3'</math> będą leżały na przecięciu się odnoszących z rzutami poziomymi krawędzi graniastosłupa <math>A', B', C'</math>. W miejscach gdzie prosta n przecina się z bokami przekroju otrzymamy poszukiwane punkty przebicia graniastosłupa prostą <math>n\ </math>,. | ||
Dla pełnego rozwiązania zadania należy ustalić widoczność prostej, która wbija się w ściany graniastosłupa. W rzucie pionowym punkty przebicia znajdują się na ścianach widocznych, zatem prosta <math>n\</math>, będzie niewidoczna jedynie na odcinku między punktami przebicia. W rzycie poziomym jeden z punktów przebicia (punkt <math>Q'</math>,) leży na ścianie niewidocznej <math>B’ C’</math>, więc prosta <math>n\</math>, będzie niewidoczna nie tylko między punktami przebicia ale również do miejsca wyjścia prostej z raniastosłupa. Niewidoczne krawędzie zaznaczono odpowiednio linią kreskową. | Dla pełnego rozwiązania zadania należy ustalić widoczność prostej, która wbija się w ściany graniastosłupa. W rzucie pionowym punkty przebicia znajdują się na ścianach widocznych, zatem prosta <math>n\ </math>, będzie niewidoczna jedynie na odcinku między punktami przebicia. W rzycie poziomym jeden z punktów przebicia (punkt <math>Q'</math>,) leży na ścianie niewidocznej <math>B’ C’</math>, więc prosta <math>n\ </math>, będzie niewidoczna nie tylko między punktami przebicia ale również do miejsca wyjścia prostej z raniastosłupa. Niewidoczne krawędzie zaznaczono odpowiednio linią kreskową. | ||
|} | |} | ||
| Linia 46: | Linia 46: | ||
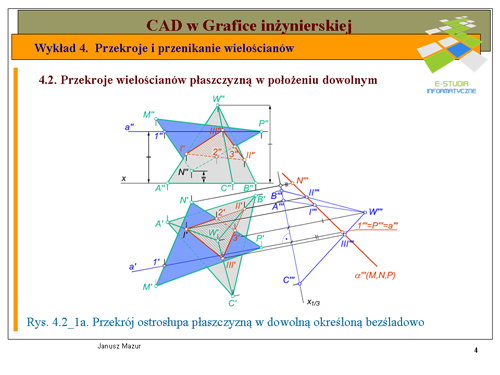
W przypadku tego zadania mamy do czynienia z wyznaczaniem przekroju ostrosłupa (linia przenikania trójkąta z ostrosłupem jest częścią przekroju ostrosłupa płaszczyzną przechodzącą przez płaszczyznę trójkąta) z płaszczyzną bezśladową, w położeniu ogólnym. | W przypadku tego zadania mamy do czynienia z wyznaczaniem przekroju ostrosłupa (linia przenikania trójkąta z ostrosłupem jest częścią przekroju ostrosłupa płaszczyzną przechodzącą przez płaszczyznę trójkąta) z płaszczyzną bezśladową, w położeniu ogólnym. | ||
Rozwiązanie zadania uprościmy sprowadzając zaprezentowany w założeniach układ do układu, w którym płaszczyzna trójkąta jest w położeniu rzutującym. Zmianę układu odniesienia przeprowadzimy za pomocą omówionej na wcześniej transformacji. W tym celu obieramy w płaszczyźnie trójkąta <math>NMP</math> prostą poziomą <math>a\</math>,. Oś <math>x_{1/3}</math> nowego układu rzutni, która zmieni układ w taki sposób, aby płaszczyzna trójkąta była w położeniu rzutującym względem nowej rzutni, będzie prostopadła do rzutu poziomego prostej poziomej <math>a'\</math>,. Kolejny etap - to dokonanie transformacji płaszczyzny trójkąta oraz ostrosłupa. Otrzymamy trzecie rzuty tych elementów przestrzennych, przy czym płaszczyzna <math>\alpha(MNP)</math> znajduje się w położeniu rzutującym względem rzutni. Wyznaczenie przekroju ostrosłupa w trzecim rzucie jest zagadnieniem prostym. Wierzchołki przekroju będą leżały na przecięciu się trzeciego rzutu płaszczyzny trójkąta <math>MNP - \alpha'''</math> z krawędziami ostrosłupa. Za pomocą odnoszących prostopadłych do osi <math>x_{1/3}</math> wyznaczymy rzuty poziome wierzchołków <math>I'</math>, <math>II'</math>, <math>III'</math>, przekroju na rzutach poziomych boków trójkąta, a następnie za pomocą odnoszących prostopadłych do osi x wyznaczymy rzuty pionowe wierzchołków przekroju <math>I''</math>, <math>II''</math>, <math>III''</math>, na rzutach pionowych boków ostrosłupa. Linia przenikania trójkąta z ostrosłupem będzie stanowiła tą część przekroju, która jest wspólna dla trójkąta i ścian ostrosłupa. | Rozwiązanie zadania uprościmy sprowadzając zaprezentowany w założeniach układ do układu, w którym płaszczyzna trójkąta jest w położeniu rzutującym. Zmianę układu odniesienia przeprowadzimy za pomocą omówionej na wcześniej transformacji. W tym celu obieramy w płaszczyźnie trójkąta <math>NMP</math> prostą poziomą <math>a\ </math>,. Oś <math>x_{1/3}</math> nowego układu rzutni, która zmieni układ w taki sposób, aby płaszczyzna trójkąta była w położeniu rzutującym względem nowej rzutni, będzie prostopadła do rzutu poziomego prostej poziomej <math>a'\ </math>,. Kolejny etap - to dokonanie transformacji płaszczyzny trójkąta oraz ostrosłupa. Otrzymamy trzecie rzuty tych elementów przestrzennych, przy czym płaszczyzna <math>\alpha(MNP)</math> znajduje się w położeniu rzutującym względem rzutni. Wyznaczenie przekroju ostrosłupa w trzecim rzucie jest zagadnieniem prostym. Wierzchołki przekroju będą leżały na przecięciu się trzeciego rzutu płaszczyzny trójkąta <math>MNP - \alpha'''</math> z krawędziami ostrosłupa. Za pomocą odnoszących prostopadłych do osi <math>x_{1/3}</math> wyznaczymy rzuty poziome wierzchołków <math>I'</math>, <math>II'</math>, <math>III'</math>, przekroju na rzutach poziomych boków trójkąta, a następnie za pomocą odnoszących prostopadłych do osi x wyznaczymy rzuty pionowe wierzchołków przekroju <math>I''</math>, <math>II''</math>, <math>III''</math>, na rzutach pionowych boków ostrosłupa. Linia przenikania trójkąta z ostrosłupem będzie stanowiła tą część przekroju, która jest wspólna dla trójkąta i ścian ostrosłupa. | ||
Zakładając, że ściany ostrosłupa oraz płaszczyzna trójkąta są nieprzezroczyste ustalamy widoczność poszczególnych linii przenikania. Podobnie jak w poprzednich zadaniach widoczność w rzucie pionowym oceniamy analizując poszczególne linie przenikania na ścianach ostrosłupa w rzucie poziomym. | Zakładając, że ściany ostrosłupa oraz płaszczyzna trójkąta są nieprzezroczyste ustalamy widoczność poszczególnych linii przenikania. Podobnie jak w poprzednich zadaniach widoczność w rzucie pionowym oceniamy analizując poszczególne linie przenikania na ścianach ostrosłupa w rzucie poziomym. | ||
| Linia 55: | Linia 55: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M4_Slajd5.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M4_Slajd5.png]] | ||
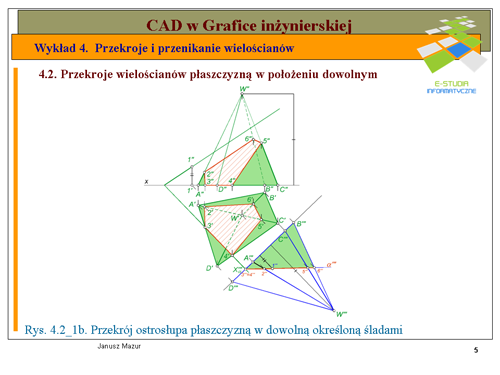
|valign="top"|Zadanie o podobnej treści można rozwiązać przyjmując dowolną płaszczyznę przekroju w postaci płaszczyzny zadanej śladami (rys.4.2_1b). W tym przypadku należy zmienić układ odniesienia za pomocą transformacji, sprowadzając płaszczyznę <math>\alpha\</math>, do położenia rzutującego. Przenosząc również ostrosłup do nowego układu za pomocą transformacji o takiej samej osi transformacji można wyznaczyć przekrój w trzecim rzucie podobnie jak w poprzednich zadaniach. | |valign="top"|Zadanie o podobnej treści można rozwiązać przyjmując dowolną płaszczyznę przekroju w postaci płaszczyzny zadanej śladami (rys.4.2_1b). W tym przypadku należy zmienić układ odniesienia za pomocą transformacji, sprowadzając płaszczyznę <math>\alpha\ </math>, do położenia rzutującego. Przenosząc również ostrosłup do nowego układu za pomocą transformacji o takiej samej osi transformacji można wyznaczyć przekrój w trzecim rzucie podobnie jak w poprzednich zadaniach. | ||
Oś transformacji obieramy prostopadle do śladu poziomego płaszczyzny <math>\alpha\</math>,. Otrzymamy trzeci rzut węzła płaszczyzny <math>X_\alpha"’</math>, który będzie jednym z punktów należących do trzeciego rzutu płaszczyzny <math>\alpha\</math>,. Należy, zatem wyznaczyć jeszcze trzeci rzut dowolnego punktu należącego do płaszczyzny <math>\alpha\</math>,, aby wyznaczyć trzeci rzut płaszczyzny. W tym celu obieramy dowolnie położony punkt <math>1"</math>, należący do śladu pionowego płaszczyzny <math>\alpha\</math>,. Drugi rzut poziomy <math>1'</math> będzie leżał na osi <math>x\</math>,. Dokonując transformacji punktu <math>1\</math>, (odmierzamy od osi transformacji wielkość równą wysokości punktu <math>1\</math>,) wyznaczymy rzut <math>1"'</math>. Punkty <math>1"'</math> i <math>X_\alpha"'</math> wyznaczą nam <math>\alpha"'</math>. Przenosimy następnie ostrosłup do nowego układu, dokonując transformacji poszczególnych wierzchołków ostrosłupa <math>ABCDW</math>. Po dokonaniu transformacji płaszczyzny <math>\alpha\</math>, i ostrosłupa można wyznaczyć trzecie rzuty wierzchołków przekroju ostrosłupa w miejscu przecięcia się <math>\alpha"'</math> z krawędziami <math>A"'W"'</math>, <math>B"'W"'</math>, <math>C"'W"'</math>, <math>D"'W"'</math> oraz z bokami podstawy (jak widać w trzecim rzucie płaszczyzna przecina również podstawę). Otrzymamy w trzecim rzuci pięć wierzchołków figury będącej przekrojem ostrosłupa (<math>2"'</math>,<math>3"'</math>,<math>4"'</math>,<math>5"'</math>,<math>6"'</math>). Powracając do układu dwu rzutni, poziomej i pionowej otrzymamy rzuty przekroju. | Oś transformacji obieramy prostopadle do śladu poziomego płaszczyzny <math>\alpha\ </math>,. Otrzymamy trzeci rzut węzła płaszczyzny <math>X_\alpha"’</math>, który będzie jednym z punktów należących do trzeciego rzutu płaszczyzny <math>\alpha\ </math>,. Należy, zatem wyznaczyć jeszcze trzeci rzut dowolnego punktu należącego do płaszczyzny <math>\alpha\ </math>,, aby wyznaczyć trzeci rzut płaszczyzny. W tym celu obieramy dowolnie położony punkt <math>1"</math>, należący do śladu pionowego płaszczyzny <math>\alpha\ </math>,. Drugi rzut poziomy <math>1'</math> będzie leżał na osi <math>x\ </math>,. Dokonując transformacji punktu <math>1\ </math>, (odmierzamy od osi transformacji wielkość równą wysokości punktu <math>1\ </math>,) wyznaczymy rzut <math>1"'</math>. Punkty <math>1"'</math> i <math>X_\alpha"'</math> wyznaczą nam <math>\alpha"'</math>. Przenosimy następnie ostrosłup do nowego układu, dokonując transformacji poszczególnych wierzchołków ostrosłupa <math>ABCDW</math>. Po dokonaniu transformacji płaszczyzny <math>\alpha\ </math>, i ostrosłupa można wyznaczyć trzecie rzuty wierzchołków przekroju ostrosłupa w miejscu przecięcia się <math>\alpha"'</math> z krawędziami <math>A"'W"'</math>, <math>B"'W"'</math>, <math>C"'W"'</math>, <math>D"'W"'</math> oraz z bokami podstawy (jak widać w trzecim rzucie płaszczyzna przecina również podstawę). Otrzymamy w trzecim rzuci pięć wierzchołków figury będącej przekrojem ostrosłupa (<math>2"'</math>,<math>3"'</math>,<math>4"'</math>,<math>5"'</math>,<math>6"'</math>). Powracając do układu dwu rzutni, poziomej i pionowej otrzymamy rzuty przekroju. | ||
Zamiast ustalenia widoczności poszczególnych krawędzi, można wyznaczyć rzuty bryły powstałej po „wygaszając” odciętą płaszczyzna przekroju część ostrosłupa. | Zamiast ustalenia widoczności poszczególnych krawędzi, można wyznaczyć rzuty bryły powstałej po „wygaszając” odciętą płaszczyzna przekroju część ostrosłupa. | ||
| Linia 71: | Linia 71: | ||
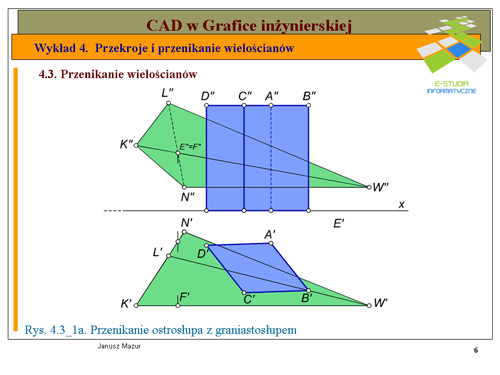
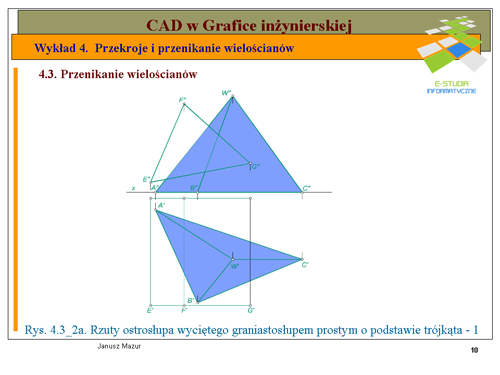
Należy wyznaczyć linię przenikania ostrosłupa <math>KLNW</math> z graniastosłupem prostym stojącym na rzutni poziomej oraz podstawie <math>ABCD</math>. | Należy wyznaczyć linię przenikania ostrosłupa <math>KLNW</math> z graniastosłupem prostym stojącym na rzutni poziomej oraz podstawie <math>ABCD</math>. | ||
Na rysunku 4.3_1a przedstawione zostały założenia do niniejszego zadania. Graniastosłup prosty, którego podstawa <math>ABCD</math> leży na rzutni poziomej ma ściany w położeniu rzutującym względem tej rzutni. Wszystkie elementy płaskie leżące na ścianach graniastosłupa, w rzucie poziomym, będą znajdowały się na rzucie poziomym boków podstawy <math>A'B'</math>, <math>B'C'</math>, <math>C'D'</math>, <math>D'A'</math>. Dla ułatwienia i czytelności rysunku nie oznaczymy górnej podstawy graniastosłupa, która jak widać z rzutu pionowego nie bierze udziału w tworzeniu linii przenikania. Położenie ostrosłupa wymaga ustalenia widoczności jego krawędzi. Widoczność tą powinniśmy ustalić w rzucie pionowym, ponieważ w rzucie poziomym odpowiednie krawędzie podstaw pokrywają się i rzuty górnych SA widoczne. W tym celu wykorzystamy punkty <math>EF\</math>, leżące odpowiednio: <math>E\</math>, na boku podstawy <math>LN\</math>, oraz <math>F\</math>, na krawędzi <math>KW\</math>, ostrosłupa. Rzuty pionowe tych punktów pokrywają się. Zważywszy, że punkt <math>F\</math>, należący do krawędzi <math>KW\</math>, ma większą głębokość (większą odległość od rzutni pionowej) można stwierdzić, iż w rzucie pionowym bok podstawy ostrosłupa <math>L''N''</math> będzie niewidoczny, co zaznaczamy linią kreskową. | Na rysunku 4.3_1a przedstawione zostały założenia do niniejszego zadania. Graniastosłup prosty, którego podstawa <math>ABCD</math> leży na rzutni poziomej ma ściany w położeniu rzutującym względem tej rzutni. Wszystkie elementy płaskie leżące na ścianach graniastosłupa, w rzucie poziomym, będą znajdowały się na rzucie poziomym boków podstawy <math>A'B'</math>, <math>B'C'</math>, <math>C'D'</math>, <math>D'A'</math>. Dla ułatwienia i czytelności rysunku nie oznaczymy górnej podstawy graniastosłupa, która jak widać z rzutu pionowego nie bierze udziału w tworzeniu linii przenikania. Położenie ostrosłupa wymaga ustalenia widoczności jego krawędzi. Widoczność tą powinniśmy ustalić w rzucie pionowym, ponieważ w rzucie poziomym odpowiednie krawędzie podstaw pokrywają się i rzuty górnych SA widoczne. W tym celu wykorzystamy punkty <math>EF\ </math>, leżące odpowiednio: <math>E\ </math>, na boku podstawy <math>LN\ </math>, oraz <math>F\ </math>, na krawędzi <math>KW\ </math>, ostrosłupa. Rzuty pionowe tych punktów pokrywają się. Zważywszy, że punkt <math>F\ </math>, należący do krawędzi <math>KW\ </math>, ma większą głębokość (większą odległość od rzutni pionowej) można stwierdzić, iż w rzucie pionowym bok podstawy ostrosłupa <math>L''N''</math> będzie niewidoczny, co zaznaczamy linią kreskową. | ||
|} | |} | ||
| Linia 82: | Linia 82: | ||
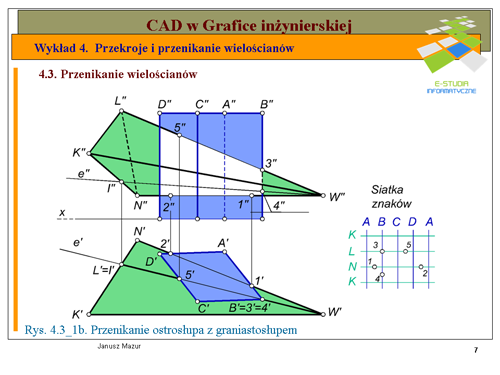
Dokonajmy, zatem analizy podanych wielościanów w aspekcie ich położenia względem siebie. | Dokonajmy, zatem analizy podanych wielościanów w aspekcie ich położenia względem siebie. | ||
Na rys. 4.3_1b, w rzucie poziomym możemy zaobserwować, które krawędzie jednego z wielościanów przebijają ściany drugiego wielościanu. Krawędź <math>A\</math>, graniastosłupa leży poza ostrosłupem i nie bierze udziału w tworzeniu poszukiwanej linii przenikania. Pozostałe krawędzie graniastosłupa przebijają ściany ostrosłupa. Krawędź <math>B\</math>, przecina krawędź <math>LW</math> oraz ścianę <math>KNW</math> ostrosłupa, krawędź <math>C\</math>, graniastosłupa przebija ściany <math>KNW</math> i <math>KLW</math> ostrosłupa. Krawędź <math>D\</math>, graniastosłupa przebija ściany <math>LNW</math> oraz <math>KNW</math>. | Na rys. 4.3_1b, w rzucie poziomym możemy zaobserwować, które krawędzie jednego z wielościanów przebijają ściany drugiego wielościanu. Krawędź <math>A\ </math>, graniastosłupa leży poza ostrosłupem i nie bierze udziału w tworzeniu poszukiwanej linii przenikania. Pozostałe krawędzie graniastosłupa przebijają ściany ostrosłupa. Krawędź <math>B\ </math>, przecina krawędź <math>LW</math> oraz ścianę <math>KNW</math> ostrosłupa, krawędź <math>C\ </math>, graniastosłupa przebija ściany <math>KNW</math> i <math>KLW</math> ostrosłupa. Krawędź <math>D\ </math>, graniastosłupa przebija ściany <math>LNW</math> oraz <math>KNW</math>. | ||
Podobnie można ocenić, które krawędzie ostrosłupa przebijają ściany graniastosłupa. Krawędź <math>NW</math> ostrosłupa przebija ściany <math>DA</math> i <math>AB</math> graniastosłupa, natomiast krawędź <math>LW</math> przebija ścianę <math>CD</math> oraz przecina (opisaną wcześniej) krawędź <math>B\</math>, graniastosłupa. Krawędź <math>KW</math> nie bierze udziału w tworzeniu linii przenikania. Po takiej analizie możemy przystąpić do wyznaczania poszczególnych punktów linii przenikania. Oznaczmy poszczególne punkty przebicia i przecięcia krawędzi ostrosłupa ze ścianami i krawędzią graniastosłupa, opisane powyżej, w rzucie poziomym kolejno punktami <math>1', 2', 3', 4', 5'</math>. Rzuty pionowe punktów <math>1'', 2'', 3'', 5''</math> znajdziemy bezpośrednio na rzucie pionowym krawędzi ostrosłupa. Jedyny problem rozwiązania stanowi rzut pionowy punktu <math>4''</math>, który znajduje się na ścianie <math>KNW</math> ostrosłupa. W celu wyznaczenia jego położenia poprowadźmy przez rzut poziomy wierzchołka <math>W'</math> ostrosłupa i rzut poziomy punktu <math>4'</math> tworzącą <math>e'</math>, leżącą na ścianie <math>K'N'W'</math>. Następnie wyznaczymy rzut pionowy tworzącej <math>e''</math>, korzystając pośrednio z rzutów punktów <math>I'</math> i <math>II''</math> przecięcia tworzącej z bokiem <math>KN</math> podstawy ostrosłupa, na rzucie pionowym <math>e''</math> wyznaczymy poszukiwany rzut pionowy punktu <math>4''</math>. W etapie <math>I\</math>, ustalone zostały punkty przebicia krawędzi ostrosłupa ze ścianami graniastosłupa. | Podobnie można ocenić, które krawędzie ostrosłupa przebijają ściany graniastosłupa. Krawędź <math>NW</math> ostrosłupa przebija ściany <math>DA</math> i <math>AB</math> graniastosłupa, natomiast krawędź <math>LW</math> przebija ścianę <math>CD</math> oraz przecina (opisaną wcześniej) krawędź <math>B\ </math>, graniastosłupa. Krawędź <math>KW</math> nie bierze udziału w tworzeniu linii przenikania. Po takiej analizie możemy przystąpić do wyznaczania poszczególnych punktów linii przenikania. Oznaczmy poszczególne punkty przebicia i przecięcia krawędzi ostrosłupa ze ścianami i krawędzią graniastosłupa, opisane powyżej, w rzucie poziomym kolejno punktami <math>1', 2', 3', 4', 5'</math>. Rzuty pionowe punktów <math>1'', 2'', 3'', 5''</math> znajdziemy bezpośrednio na rzucie pionowym krawędzi ostrosłupa. Jedyny problem rozwiązania stanowi rzut pionowy punktu <math>4''</math>, który znajduje się na ścianie <math>KNW</math> ostrosłupa. W celu wyznaczenia jego położenia poprowadźmy przez rzut poziomy wierzchołka <math>W'</math> ostrosłupa i rzut poziomy punktu <math>4'</math> tworzącą <math>e'</math>, leżącą na ścianie <math>K'N'W'</math>. Następnie wyznaczymy rzut pionowy tworzącej <math>e''</math>, korzystając pośrednio z rzutów punktów <math>I'</math> i <math>II''</math> przecięcia tworzącej z bokiem <math>KN</math> podstawy ostrosłupa, na rzucie pionowym <math>e''</math> wyznaczymy poszukiwany rzut pionowy punktu <math>4''</math>. W etapie <math>I\ </math>, ustalone zostały punkty przebicia krawędzi ostrosłupa ze ścianami graniastosłupa. | ||
W celu określenia kolejności połączenia punktów tworzących linie przenikania zbudujemy tzw. '''siatkę znaków'''. Rozetnijmy poszczególne wielościany wzdłuż jednej z krawędzi (najlepiej według krawędzi niebiorącej udziału w tworzeniu linii przenikania) i oznaczmy te krawędzie symbolicznie na przedstawionej siatce, powtarzając pierwszą krawędź tak, aby zamknąć powierzchnię boczną danego wielościanu. Na tak stworzonej siatce nanosimy symbolicznie poszczególne punkty linii przenikania. Np. punkt <math>1\</math>, znajduje się na krawędzi <math>N\</math>, ostrosłupa oraz ścianie <math>AB</math> graniastosłupa. Podobnie postępujemy z następnymi punktami. | W celu określenia kolejności połączenia punktów tworzących linie przenikania zbudujemy tzw. '''siatkę znaków'''. Rozetnijmy poszczególne wielościany wzdłuż jednej z krawędzi (najlepiej według krawędzi niebiorącej udziału w tworzeniu linii przenikania) i oznaczmy te krawędzie symbolicznie na przedstawionej siatce, powtarzając pierwszą krawędź tak, aby zamknąć powierzchnię boczną danego wielościanu. Na tak stworzonej siatce nanosimy symbolicznie poszczególne punkty linii przenikania. Np. punkt <math>1\ </math>, znajduje się na krawędzi <math>N\ </math>, ostrosłupa oraz ścianie <math>AB</math> graniastosłupa. Podobnie postępujemy z następnymi punktami. | ||
|} | |} | ||
| Linia 96: | Linia 96: | ||
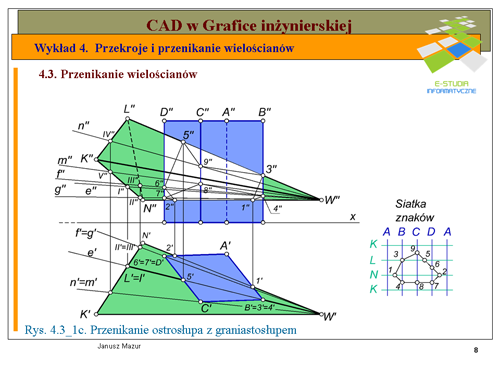
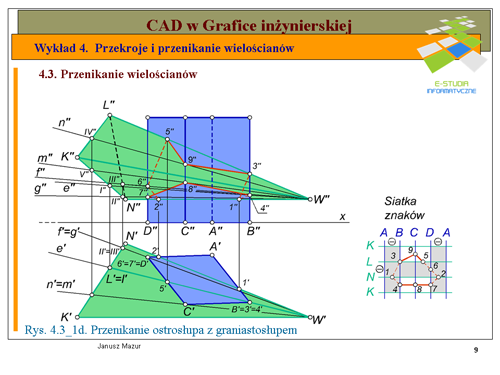
|valign="top"|W etapie II zajmiemy się punktami przecięcia krawędzi graniastosłupa ze ścianami ostrosłupa (patrz rys. 4.3_1c). | |valign="top"|W etapie II zajmiemy się punktami przecięcia krawędzi graniastosłupa ze ścianami ostrosłupa (patrz rys. 4.3_1c). | ||
Kolejne punkty przecięcia krawędzi graniastosłupa ze ścianami ostrosłupa to: punkty <math>6\</math>, i <math>7\</math>, przebicia krawędzi <math>D\</math>, ze ścianami odpowiednio <math>NLW</math> i <math>NKW</math> oraz punkty <math>8\</math>, i <math>9\</math>, przebicia krawędzi <math>C\</math>, ze ścianami <math>KLW</math> i <math>KNW</math>. Rzuty pionowe tych punktów wyznaczymy po ustaleniu rzutów pionowych poszczególnych tworzących przechodzących przez te punkty. | Kolejne punkty przecięcia krawędzi graniastosłupa ze ścianami ostrosłupa to: punkty <math>6\ </math>, i <math>7\ </math>, przebicia krawędzi <math>D\ </math>, ze ścianami odpowiednio <math>NLW</math> i <math>NKW</math> oraz punkty <math>8\ </math>, i <math>9\ </math>, przebicia krawędzi <math>C\ </math>, ze ścianami <math>KLW</math> i <math>KNW</math>. Rzuty pionowe tych punktów wyznaczymy po ustaleniu rzutów pionowych poszczególnych tworzących przechodzących przez te punkty. | ||
Końcowym akcentem tego etapu jest wyznaczanie linii przenikania, a więc ustalenie, które punkty należy połączyć ze sobą tak, aby utworzyły zamkniętą linię przenikania. Powracamy zatem do '''siatki znaków''' Zasada łączenia ze sobą poszczególnych punktów polega na łączeniu ze sobą jedynie w obrębie jednego kwadratu. Powstała, zatem zamknięta linia przenikania. Może się zdarzyć, że otrzymamy dwie, pozornie otwarte linie przenikania, wtedy, gdy przecięcie wielościanu nastąpi wzdłuż krawędzi zaangażowanej w procesie konstrukcji linii przenikania. Pamiętając jednak, że powierzchnie boczne wielościanów są zamknięte oraz, że na końcu siatki powtarzamy pierwsza krawędź, zawsze otrzymamy linie zamkniętą. Tak otrzymane połączenia punktów linii przenikania nanosimy następnie, cienką linią, na rysunek konstrukcyjny. | Końcowym akcentem tego etapu jest wyznaczanie linii przenikania, a więc ustalenie, które punkty należy połączyć ze sobą tak, aby utworzyły zamkniętą linię przenikania. Powracamy zatem do '''siatki znaków''' Zasada łączenia ze sobą poszczególnych punktów polega na łączeniu ze sobą jedynie w obrębie jednego kwadratu. Powstała, zatem zamknięta linia przenikania. Może się zdarzyć, że otrzymamy dwie, pozornie otwarte linie przenikania, wtedy, gdy przecięcie wielościanu nastąpi wzdłuż krawędzi zaangażowanej w procesie konstrukcji linii przenikania. Pamiętając jednak, że powierzchnie boczne wielościanów są zamknięte oraz, że na końcu siatki powtarzamy pierwsza krawędź, zawsze otrzymamy linie zamkniętą. Tak otrzymane połączenia punktów linii przenikania nanosimy następnie, cienką linią, na rysunek konstrukcyjny. | ||
| Linia 125: | Linia 125: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M4_Slajd11.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M4_Slajd11.png]] | ||
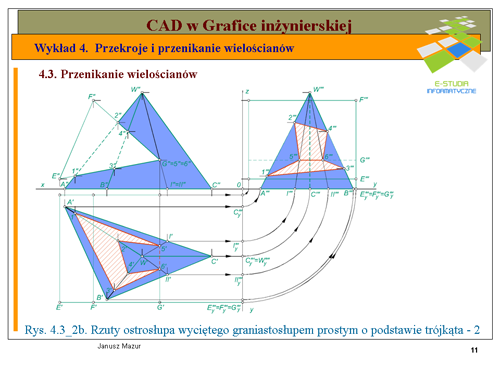
|valign="top"|W pierwszej kolejności uzupełniamy założenia o wyznaczenie trzecich rzutów ostrosłupa i graniastosłupa wycinającego (rys.4.3_2b). Rzutowanie ostrosłupa na trzecia, prostopadłą do rzutni <math>\Pi_1</math> i <math>\Pi_2</math> rozpoczynamy od przeniesienia rzutu podstawy na oś y między rzutnią <math>\Pi_1</math> a rzutnią <math>\Pi_3</math>. Po obrocie osi <math>y\</math>, do pokrycia się z osią <math>x\</math>, wyznaczymy (po rozwinięciu układu trzech rzutni) trzeci rzut podstawy <math>A"'</math>,<math>B"'</math>,<math>C"'</math>. Podobnie czynimy z wierzchołkiem <math>W\</math>,. Po obrocie i przeniesieniu rzutu poziomego do trzeciej rzutni, odmierzamy wysokość ostrosłupa, która oczywiście wyznaczy nam trzeci rzut wierzchołka <math>W"'</math>. | |valign="top"|W pierwszej kolejności uzupełniamy założenia o wyznaczenie trzecich rzutów ostrosłupa i graniastosłupa wycinającego (rys.4.3_2b). Rzutowanie ostrosłupa na trzecia, prostopadłą do rzutni <math>\Pi_1</math> i <math>\Pi_2</math> rozpoczynamy od przeniesienia rzutu podstawy na oś y między rzutnią <math>\Pi_1</math> a rzutnią <math>\Pi_3</math>. Po obrocie osi <math>y\ </math>, do pokrycia się z osią <math>x\ </math>, wyznaczymy (po rozwinięciu układu trzech rzutni) trzeci rzut podstawy <math>A"'</math>,<math>B"'</math>,<math>C"'</math>. Podobnie czynimy z wierzchołkiem <math>W\ </math>,. Po obrocie i przeniesieniu rzutu poziomego do trzeciej rzutni, odmierzamy wysokość ostrosłupa, która oczywiście wyznaczy nam trzeci rzut wierzchołka <math>W"'</math>. | ||
Podobnie przenosimy do trzeciej rzutni graniastosłup <math>EFG</math>, którego krawędzie w trzecim rzucie będą równoległe do osi <math>y\</math>, po obrocie. | Podobnie przenosimy do trzeciej rzutni graniastosłup <math>EFG</math>, którego krawędzie w trzecim rzucie będą równoległe do osi <math>y\ </math>, po obrocie. | ||
Zarówno w rzutach pionowym i poziomym, jak również w rzucie trzecim ustalamy widoczność krawędzi analizując każdy rzut z kierunku prostopadłego do określonej rzutni. Widoczność krawędzi w rzutach pionowym i bocznym analizujemy poprzez obserwacje rzutu poziomego z kierunku prostopadłego do osi odpowiednio <math>x\</math>, i <math>y\</math>,. | Zarówno w rzutach pionowym i poziomym, jak również w rzucie trzecim ustalamy widoczność krawędzi analizując każdy rzut z kierunku prostopadłego do określonej rzutni. Widoczność krawędzi w rzutach pionowym i bocznym analizujemy poprzez obserwacje rzutu poziomego z kierunku prostopadłego do osi odpowiednio <math>x\ </math>, i <math>y\ </math>,. | ||
Wyznaczenie linii przenikania rozpoczynamy od rzutu pionowego obu wielościanów. Wyznaczamy w rzucie pionowym punkty przebicia krawędzi ostrosłupa z e ścianami graniastosłupa. Rzutujący charakter ścian graniastosłupa ułatwia nam wyznaczenie rzutów pionowych punktów przebicia krawędzi ostrosłupa ze ścianami graniastosłupa. Możemy, zatem określić rzuty pionowe punktów przebicia <math>1"</math>,<math>2"</math>,<math>3"</math>,<math>4"</math>. Punkt <math>G"</math> graniastosłupa będzie pokrywał się z dwoma rzutami punktów przebicia tej krawędzi graniastosłupa ze ścianami <math>AC</math> i <math>BC</math> ostrosłupa, a mianowicie <math>5"</math> i <math>6"</math>. Wyznaczono, zatem wszystkie punkty przebicia krawędzi jednego wielościanu ze ścianami drugiego wielościanu i odwrotnie. | Wyznaczenie linii przenikania rozpoczynamy od rzutu pionowego obu wielościanów. Wyznaczamy w rzucie pionowym punkty przebicia krawędzi ostrosłupa z e ścianami graniastosłupa. Rzutujący charakter ścian graniastosłupa ułatwia nam wyznaczenie rzutów pionowych punktów przebicia krawędzi ostrosłupa ze ścianami graniastosłupa. Możemy, zatem określić rzuty pionowe punktów przebicia <math>1"</math>,<math>2"</math>,<math>3"</math>,<math>4"</math>. Punkt <math>G"</math> graniastosłupa będzie pokrywał się z dwoma rzutami punktów przebicia tej krawędzi graniastosłupa ze ścianami <math>AC</math> i <math>BC</math> ostrosłupa, a mianowicie <math>5"</math> i <math>6"</math>. Wyznaczono, zatem wszystkie punkty przebicia krawędzi jednego wielościanu ze ścianami drugiego wielościanu i odwrotnie. | ||
Aktualna wersja na dzień 12:03, 5 wrz 2023

|
Wykład 4. Przekroje i przenikanie wielościanów |

|