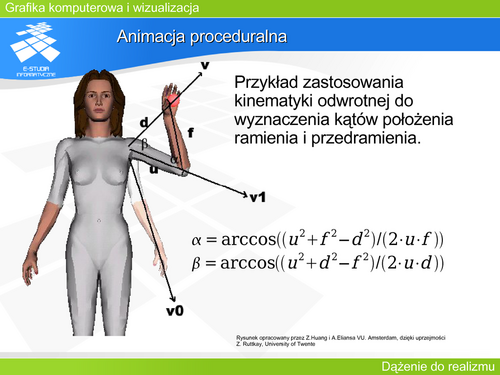
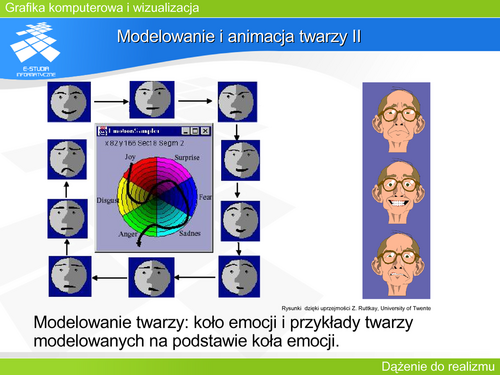
GKIW Moduł 10 - Dążenie do realizmu: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „,</math>” na „</math>,” |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| Linia 114: | Linia 114: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd12n.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd12n.png|thumb|500px]] | ||
|valign="top"|Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, która będzie odkształcona. Niech <math>B(u,v)</math> opisuje zaburzenie (teksturę). Wektor normalny <math>\vec{N}\</math>, do powierzchni <math>S(u,v)\</math>, można wyznaczyć jako: | |valign="top"|Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, która będzie odkształcona. Niech <math>B(u,v)</math> opisuje zaburzenie (teksturę). Wektor normalny <math>\vec{N}\ </math>, do powierzchni <math>S(u,v)\ </math>, można wyznaczyć jako: | ||
:<math>\vec{N}=\frac{\partial S(u,v)}{\partial u}\times\frac{\partial S(u,v)}{\partial v}</math> | :<math>\vec{N}=\frac{\partial S(u,v)}{\partial u}\times\frac{\partial S(u,v)}{\partial v}</math> | ||
| Linia 136: | Linia 136: | ||
:<math>\vec{N}'=\vec{N}+\vec{D}</math> | :<math>\vec{N}'=\vec{N}+\vec{D}</math> | ||
Przy czym <math>\vec{D}\</math>, jest wektorem zaburzenia: | Przy czym <math>\vec{D}\ </math>, jest wektorem zaburzenia: | ||
:<math>\vec{D}=\frac{\partial B(u,v)}{\partial u}\cdot \vec{S}-\frac{\partial B(u,v)}{\partial v}\cdot \vec{T}</math> | :<math>\vec{D}=\frac{\partial B(u,v)}{\partial u}\cdot \vec{S}-\frac{\partial B(u,v)}{\partial v}\cdot \vec{T}</math> | ||
gdzie <math>\vec{S}\</math>, i <math>\vec{T}\</math>, są wektorami stycznymi do powierzchni <math>S(u,v)\</math>,. | gdzie <math>\vec{S}\ </math>, i <math>\vec{T}\ </math>, są wektorami stycznymi do powierzchni <math>S(u,v)\ </math>,. | ||
Takie rozwiązanie daje bardzo prostą możliwość definicji wektora normalnego odkształconej powierzchni za pomocą wektorów zaburzenia. Wadą zaproponowanej przez Blinna metody jest aproksymacja wektora normalnego. Stąd powstało wiele różnych realizacji tej metody, wykorzystujących różne warianty uproszczenia. Znane są również próby aplikacji sprzętowych mapowania nierówności Blinna. | Takie rozwiązanie daje bardzo prostą możliwość definicji wektora normalnego odkształconej powierzchni za pomocą wektorów zaburzenia. Wadą zaproponowanej przez Blinna metody jest aproksymacja wektora normalnego. Stąd powstało wiele różnych realizacji tej metody, wykorzystujących różne warianty uproszczenia. Znane są również próby aplikacji sprzętowych mapowania nierówności Blinna. | ||
| Linia 158: | Linia 158: | ||
Techniką dającą dobre efekty w takiej sytuacji jest mapowanie przesunięć. | Techniką dającą dobre efekty w takiej sytuacji jest mapowanie przesunięć. | ||
Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, <math>P\</math>, będzie punktem na tej powierzchni, a <math>\vec{N}\</math>, będzie wektorem normalnym do powierzchni <math>S(u,v)\</math>,. Niech funkcja <math>f(P)\</math>, opisuje przesunięcie punktu powierzchni <math>S(u,v)\</math>,. | Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, <math>P\ </math>, będzie punktem na tej powierzchni, a <math>\vec{N}\ </math>, będzie wektorem normalnym do powierzchni <math>S(u,v)\ </math>,. Niech funkcja <math>f(P)\ </math>, opisuje przesunięcie punktu powierzchni <math>S(u,v)\ </math>,. | ||
Wtedy dla każdego punktu <math>P\</math>, | Wtedy dla każdego punktu <math>P\ </math>, | ||
:<math>P'=P+f(P)\cdot \vec{N}</math> | :<math>P'=P+f(P)\cdot \vec{N}</math> | ||
Aktualna wersja na dzień 12:03, 5 wrz 2023
Wykład
 |
 |
Literatura
 |
 |