Pr-1st-1.1-m10-Slajd09: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „ </math>” na „</math>” |
||
| Linia 11: | Linia 11: | ||
Równość liczników wiadomości wysłanych i odebranych mogłoby sugerować, że wszystkie kanały są puste, i że tym samym wystąpiło zakończenie. Zauważmy jednak, że w żadnym momencie <math>\tau</math> z przedziału obserwacji | Równość liczników wiadomości wysłanych i odebranych mogłoby sugerować, że wszystkie kanały są puste, i że tym samym wystąpiło zakończenie. Zauważmy jednak, że w żadnym momencie <math>\tau</math> z przedziału obserwacji | ||
<math>\left \langle \tau _b, \tau _e \right \rangle </math> kanały nie są jednocześnie puste, a więc <math>SC(\tau) \ne RC(\tau)</math> dla każdego <math>\tau, \tau \in \left \langle \tau _b, \tau _e \right \rangle</math>. Powstaje zatem problem, czy i kiedy na podstawie faktu, że <math>SC^{*}= RC^{*} | <math>\left \langle \tau _b, \tau _e \right \rangle</math> kanały nie są jednocześnie puste, a więc <math>SC(\tau) \ne RC(\tau)</math> dla każdego <math>\tau, \tau \in \left \langle \tau _b, \tau _e \right \rangle</math>. Powstaje zatem problem, czy i kiedy na podstawie faktu, że <math>SC^{*}= RC^{*} | ||
</math> można wnioskować o wystąpieniu zakończenia. | </math> można wnioskować o wystąpieniu zakończenia. | ||
Aktualna wersja na dzień 10:45, 5 wrz 2023
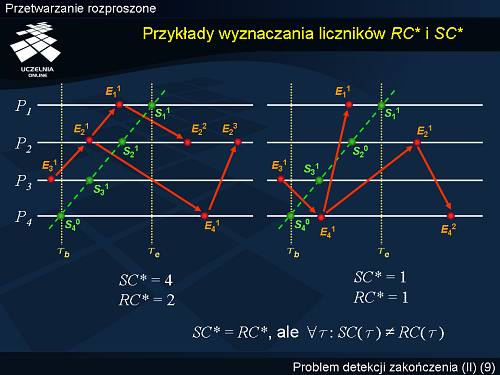
Przykłady wyznaczania liczników RC^{*} i SC^{*}
Dla ilustracji przedstawionej koncepcji rozważmy obecnie dwa przykłady przedstawione na slajdzie. Na przykładzie po lewej stronie slajdu, proces detekcji rozpoczynany jest w chwili przez monitor procesu . W chwili tej oraz
. Znacznik jest przesyłany następnie do monitora procesu , który odczytuje wartości oraz . Następnie, kolejno wyznaczane są wartości: , ,
, . W efekcie w chwili otrzymujemy a .
Z kolei sytuacja na przykładzie po prawej stronie slajdu jest następująca: . Tym samym a .
Równość liczników wiadomości wysłanych i odebranych mogłoby sugerować, że wszystkie kanały są puste, i że tym samym wystąpiło zakończenie. Zauważmy jednak, że w żadnym momencie z przedziału obserwacji kanały nie są jednocześnie puste, a więc dla każdego . Powstaje zatem problem, czy i kiedy na podstawie faktu, że można wnioskować o wystąpieniu zakończenia.