MO Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „ </math>” na „</math>” |
m Zastępowanie tekstu – „<math> ” na „<math>” |
||
| Linia 153: | Linia 153: | ||
{| border="0" cellpadding="4" width="125%" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd21.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd21.png|thumb|500px]] | ||
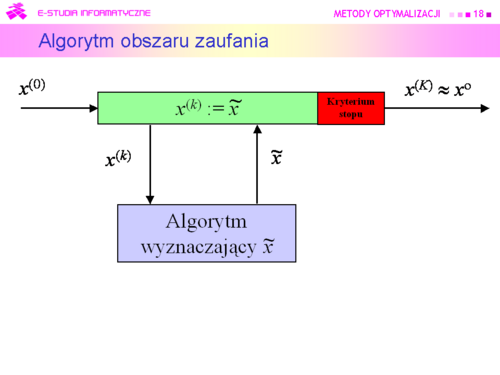
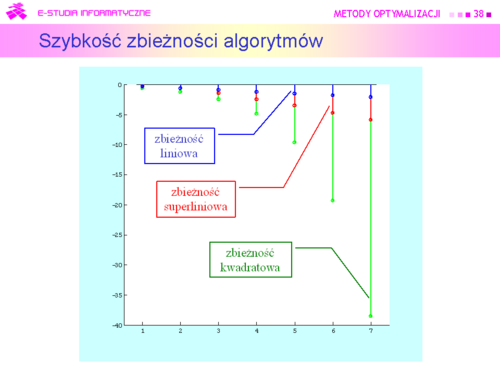
|valign="top"|Ciąg prostszych zadań daje ciąg rozwiązań {<math> x^{(k)}</math>}<math>_{k = 0}^\infty}</math> Naturalne pytanie które postawiliśmy, to kiedy go uciąć – '''które <math>k</math> uznać za ostatnie''', dające rozwiązanie z dostateczną dokładnością. Był to zasygnalizowany problem testu stopu. Związane z tym problemem jest pytanie drugie – '''czy wygenerowany ciąg''' w ogóle '''jest zbieżny''', a gdy jest, to '''czy jego granica jest rozwiązaniem zadania optymalizacji ?''' Jest to pytanie teoretyczne i odpowiemy na nie po konkretyzacji algorytmu w wykładzie siódmym. | |valign="top"|Ciąg prostszych zadań daje ciąg rozwiązań {<math>x^{(k)}</math>}<math>_{k = 0}^\infty}</math> Naturalne pytanie które postawiliśmy, to kiedy go uciąć – '''które <math>k</math> uznać za ostatnie''', dające rozwiązanie z dostateczną dokładnością. Był to zasygnalizowany problem testu stopu. Związane z tym problemem jest pytanie drugie – '''czy wygenerowany ciąg''' w ogóle '''jest zbieżny''', a gdy jest, to '''czy jego granica jest rozwiązaniem zadania optymalizacji ?''' Jest to pytanie teoretyczne i odpowiemy na nie po konkretyzacji algorytmu w wykładzie siódmym. | ||
|} | |} | ||
---- | ---- | ||
Aktualna wersja na dzień 10:34, 5 wrz 2023
 |
 |
 |
 |
 |
Algorytm może być:
a następnie przeszukiwać je tak jak poprzednio. |
 |
 |
Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm wymyślony przez:
|
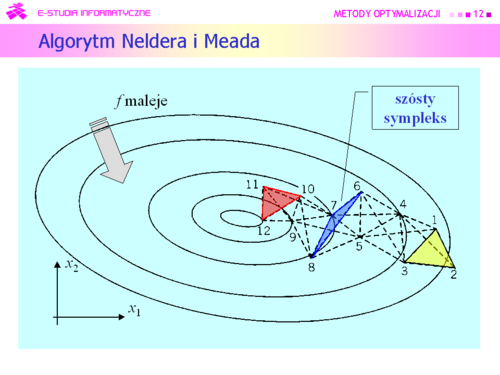 |
Dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo ładnie. |
 |
Metody oparte na takim rozumowaniu od połowy lat dziewięćdziesiątych XX w nazywa się:
(Trust region methods) |
 |
 |
 |
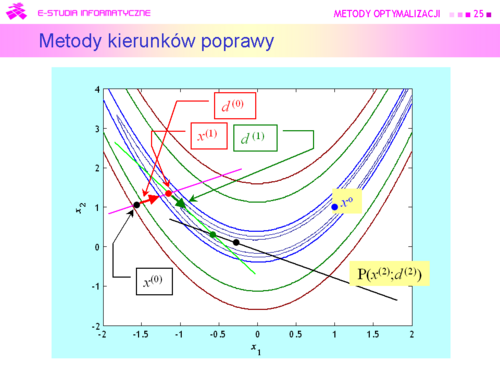
Tu oczywistym pomysłem jest wykorzystanie rozważań teoretycznych, pokazujących związek kierunku poprawy z gradientem (lemat 4.3).
Algorytm będzie zatem wykorzystywał: |
 |
 |
 |
 |
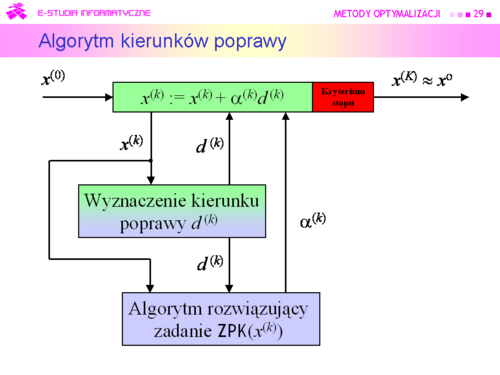
Teraz zauważmy tylko, że test stopu powinien zawierać dwa warunki: jeden badający “optymalność” kolejnego punktu, a drugi określający maksymalną liczbę iteracji. |
 |
 |
 |
 |
 |
 |