CWGI Moduł 1: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „ \</math>” na „</math>” |
m Zastępowanie tekstu – „<math> ” na „<math>” |
||
| Linia 114: | Linia 114: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd9.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd9.png]] | ||
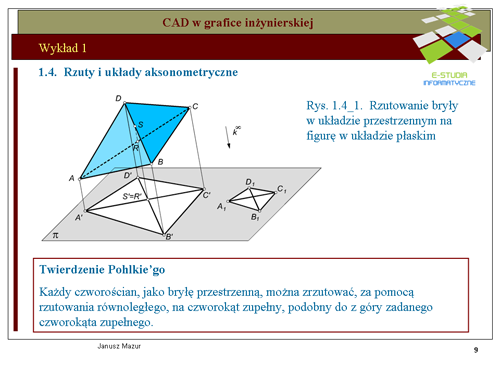
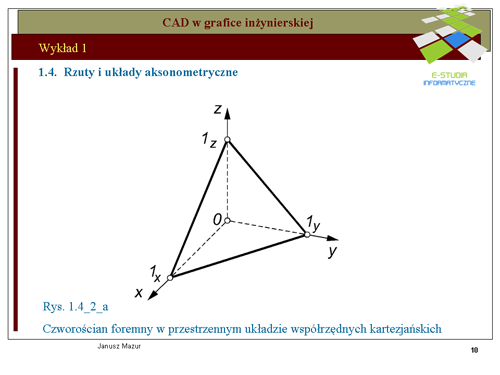
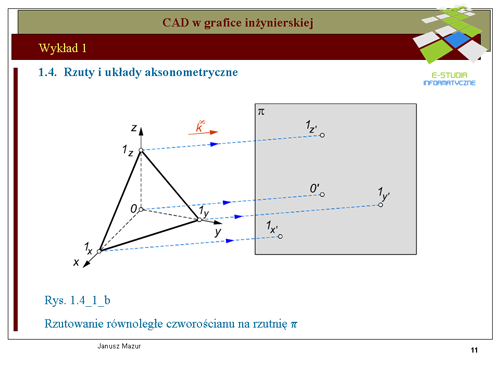
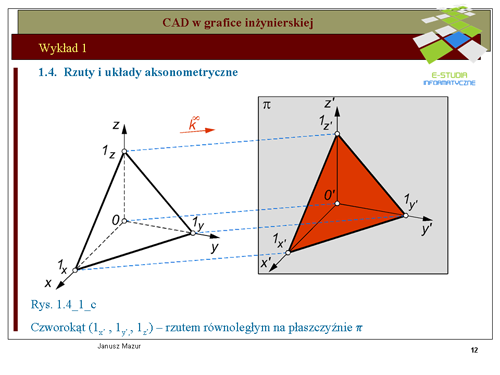
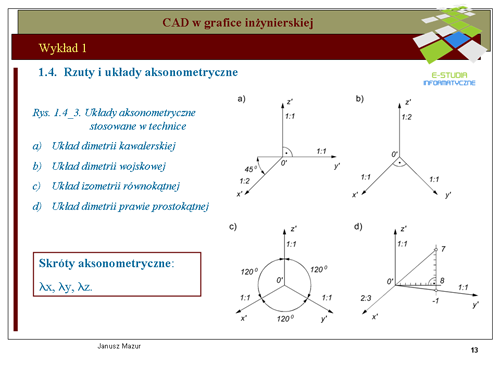
|valign="top"|Znany z geometrii elementarnej układ osi współrzędnych, zwany układem kartezjańskim, jest układem przestrzennym i składa się z osi <math> x, y, z</math> oraz początku układu współrzędnych 0. Osie przecinają się w punkcie początkowym każdej z nich pod kątami <math>90^o\</math>, względem siebie. Umieszczony w takim układzie punkt <math>P\</math>, będzie miał współrzędne <math>P(x_o, y_o, z_o)</math>. Analogicznie można zdefiniować położenie wektora i innych elementów w przestrzeni. Rzuty aksonometryczne są formą rzutów równoległych, które pozwalają przetransponować układ przestrzenny <math>0xyz</math> na układ płaski, a więc układ umożliwiający odwzorowanie tworów przestrzennych na płaszczyźnie. Takim zagadnieniem jesteśmy zainteresowani z punktu widzenia graficznego zapisu konstrukcji. Rozwijając teorię rzutowania równoległego przyjmiemy twierdzenie '''Pohlke'go''', które otworzy możliwości wyodrębnionego zapisu tworów przestrzennych zwanego '''rzutem aksonometrycznym'''. Twierdzenie to umożliwia przenoszenie brył przestrzennych do zupełnie dowolnych układów płaskich zwanych układami aksonometrycznymi. Stanowi to dla inżyniera źródło możliwości różnorodnego eksponowania swoich twórczych projektów. | |valign="top"|Znany z geometrii elementarnej układ osi współrzędnych, zwany układem kartezjańskim, jest układem przestrzennym i składa się z osi <math>x, y, z</math> oraz początku układu współrzędnych 0. Osie przecinają się w punkcie początkowym każdej z nich pod kątami <math>90^o\</math>, względem siebie. Umieszczony w takim układzie punkt <math>P\</math>, będzie miał współrzędne <math>P(x_o, y_o, z_o)</math>. Analogicznie można zdefiniować położenie wektora i innych elementów w przestrzeni. Rzuty aksonometryczne są formą rzutów równoległych, które pozwalają przetransponować układ przestrzenny <math>0xyz</math> na układ płaski, a więc układ umożliwiający odwzorowanie tworów przestrzennych na płaszczyźnie. Takim zagadnieniem jesteśmy zainteresowani z punktu widzenia graficznego zapisu konstrukcji. Rozwijając teorię rzutowania równoległego przyjmiemy twierdzenie '''Pohlke'go''', które otworzy możliwości wyodrębnionego zapisu tworów przestrzennych zwanego '''rzutem aksonometrycznym'''. Twierdzenie to umożliwia przenoszenie brył przestrzennych do zupełnie dowolnych układów płaskich zwanych układami aksonometrycznymi. Stanowi to dla inżyniera źródło możliwości różnorodnego eksponowania swoich twórczych projektów. | ||
| Linia 188: | Linia 188: | ||
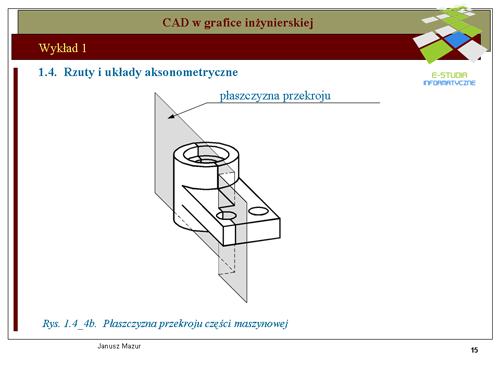
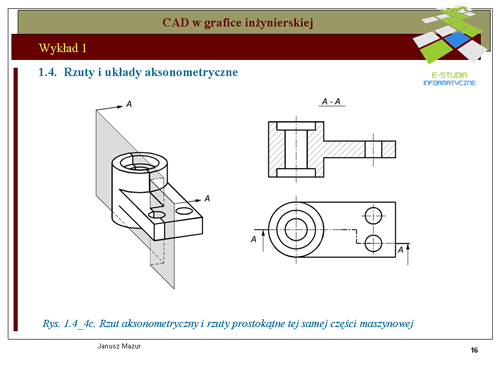
|valign="top"|Rzutowanie prostokątne elementów przestrzennych jest podstawową formą odwzorowań stosowanych w grafice inżynierskiej. Zastosowanie trzech wzajemnie prostopadłych rzutni umożliwia jednoznaczne odwzorowanie elementów przestrzennych na płaszczyźnie i odwrotnie. Tego typu rzutowanie jest podstawą '''graficznego i komputerowego zapisu konstrukcji'''. Rzut prostokątny jest rodzajem rzutu równoległego. Zatem znane są zasady rzutowania prostokątnego. Umieszczony twór przestrzenny rzutowany jest za pomocą promieni rzutujących prostopadłych do rzutni. | |valign="top"|Rzutowanie prostokątne elementów przestrzennych jest podstawową formą odwzorowań stosowanych w grafice inżynierskiej. Zastosowanie trzech wzajemnie prostopadłych rzutni umożliwia jednoznaczne odwzorowanie elementów przestrzennych na płaszczyźnie i odwrotnie. Tego typu rzutowanie jest podstawą '''graficznego i komputerowego zapisu konstrukcji'''. Rzut prostokątny jest rodzajem rzutu równoległego. Zatem znane są zasady rzutowania prostokątnego. Umieszczony twór przestrzenny rzutowany jest za pomocą promieni rzutujących prostopadłych do rzutni. | ||
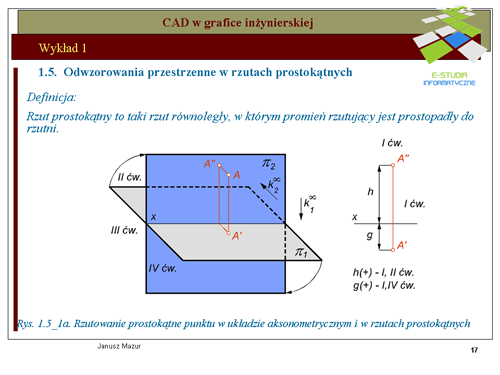
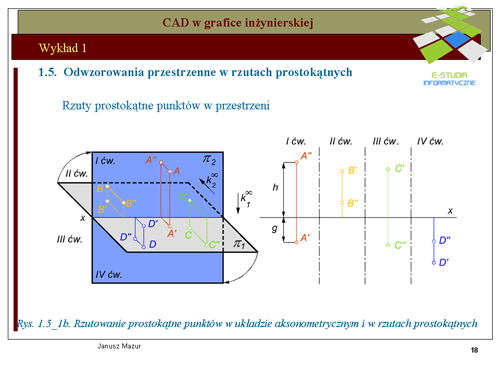
Na rys. rys. 1.5_1a przedstawiono zasady tworzenia rzutu prostokątnego punktu A w układzie dwu rzutni wzajemnie do siebie prostopadłych. Zasadę tworzenia rzutów prostokątnych przedstawiono również w rzutach aksonometrycznych, w celu pełniejszego zrozumienia omawianego zagadnienia. Rzutowanie prostokątne polega na generacji promieni rzutujących prostopadłych do rzutni, przez elementy tworów przestrzennych (w tym przypadku – punktu<math> A\</math>,) | Na rys. rys. 1.5_1a przedstawiono zasady tworzenia rzutu prostokątnego punktu A w układzie dwu rzutni wzajemnie do siebie prostopadłych. Zasadę tworzenia rzutów prostokątnych przedstawiono również w rzutach aksonometrycznych, w celu pełniejszego zrozumienia omawianego zagadnienia. Rzutowanie prostokątne polega na generacji promieni rzutujących prostopadłych do rzutni, przez elementy tworów przestrzennych (w tym przypadku – punktu<math>A\</math>,) | ||
|} | |} | ||
Wersja z 10:32, 5 wrz 2023