Matematyka dyskretna 1/Ćwiczenia 14: Grafy III: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „\displaystyle ” na „” |
m Zastępowanie tekstu – „ </math>” na „</math>” |
||
| Linia 3: | Linia 3: | ||
{{cwiczenie|1|cw 1| | {{cwiczenie|1|cw 1| | ||
Przedstaw graf nieplanarny, który nie jest homeomorficzny ani ściągalny | Przedstaw graf nieplanarny, który nie jest homeomorficzny ani ściągalny | ||
do <math>\mathcal{K}_{5} </math> oraz <math>\mathcal{K}_{3,3} </math> . | do <math>\mathcal{K}_{5}</math> oraz <math>\mathcal{K}_{3,3}</math> . | ||
Dlaczego nie jest to kontrprzykład dla twierdzeń [[Matematyka dyskretna 1/Wykład 14: Grafy III#tw_14.2|14.2]] oraz [[Matematyka dyskretna 1/Wykład 14: Grafy III#tw_14.3|14.3]]? | Dlaczego nie jest to kontrprzykład dla twierdzeń [[Matematyka dyskretna 1/Wykład 14: Grafy III#tw_14.2|14.2]] oraz [[Matematyka dyskretna 1/Wykład 14: Grafy III#tw_14.3|14.3]]? | ||
| Linia 15: | Linia 15: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
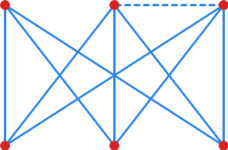
[[File:Cw grafy nieplanarny.svg|300x150px|thumb|right" id="cw_grafy_nieplanarny|1. Graf <math>\mathbf{G} </math>]] | [[File:Cw grafy nieplanarny.svg|300x150px|thumb|right" id="cw_grafy_nieplanarny|1. Graf <math>\mathbf{G}</math>]] | ||
Graf <math>\mathbf{G} </math> przedstawiony na [[#cw grafy nieplanarny|rysunku 1]] nie jest planarny | Graf <math>\mathbf{G}</math> przedstawiony na [[#cw grafy nieplanarny|rysunku 1]] nie jest planarny | ||
i ponadto nie jest homeomorficzny ani ściągalny do <math>\mathcal{K}_{5} </math> ani <math>\mathcal{K}_{3,3} </math> . | i ponadto nie jest homeomorficzny ani ściągalny do <math>\mathcal{K}_{5}</math> ani <math>\mathcal{K}_{3,3}</math> . | ||
W Twierdzeniach [[Matematyka dyskretna 1/Wykład 14: Grafy III#tw_14.2|14.2]] oraz [[Matematyka dyskretna 1/Wykład 14: Grafy III#tw_14.3|14.3]] jest mowa, że aby graf był planarny, to dowolny podgraf musi spełniać określone warunki. | W Twierdzeniach [[Matematyka dyskretna 1/Wykład 14: Grafy III#tw_14.2|14.2]] oraz [[Matematyka dyskretna 1/Wykład 14: Grafy III#tw_14.3|14.3]] jest mowa, że aby graf był planarny, to dowolny podgraf musi spełniać określone warunki. | ||
Tak więc przed szukaniem zabronionych struktur możemy więc usunąć z grafu dowolną liczbę wierzchołków oraz krawędzi. Faktycznie, po usunięciu czerwonej krawędzi graf <math>\mathbf{G} </math> staje się pełnym grafem dwudzielnym <math>\mathcal{K}_{3,3} </math> . | Tak więc przed szukaniem zabronionych struktur możemy więc usunąć z grafu dowolną liczbę wierzchołków oraz krawędzi. Faktycznie, po usunięciu czerwonej krawędzi graf <math>\mathbf{G}</math> staje się pełnym grafem dwudzielnym <math>\mathcal{K}_{3,3}</math> . | ||
</div></div> | </div></div> | ||
| Linia 32: | Linia 32: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Zauważ, że każdy wielościan można tak zrzutować na płąszczyznę <math>\mathbb{R}^2 </math> , | Zauważ, że każdy wielościan można tak zrzutować na płąszczyznę <math>\mathbb{R}^2</math> , | ||
by rzut ten reprezentował graf planarny. | by rzut ten reprezentował graf planarny. | ||
Skorzystaj z Twierdzenia [[Matematyka dyskretna 1/Wykład 14: Grafy III#tw_14.4|14.4]]. | Skorzystaj z Twierdzenia [[Matematyka dyskretna 1/Wykład 14: Grafy III#tw_14.4|14.4]]. | ||
| Linia 39: | Linia 39: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Przyjmijmy oznaczenia: | Przyjmijmy oznaczenia: | ||
* <math>x </math> - liczba ścian pięciokątnych, | * <math>x</math> - liczba ścian pięciokątnych, | ||
* <math>y </math> - liczba ścian sześciokątnych. | * <math>y</math> - liczba ścian sześciokątnych. | ||
Suma <math>x+y </math> to liczba wszystkich ścian, | Suma <math>x+y</math> to liczba wszystkich ścian, | ||
więc na mocy twierdzenia [[Matematyka dyskretna 1/Wykład 14: Grafy III#tw_14.4|14.4]] otrzymujemy | więc na mocy twierdzenia [[Matematyka dyskretna 1/Wykład 14: Grafy III#tw_14.4|14.4]] otrzymujemy | ||
| Linia 60: | Linia 60: | ||
Podstawiając tę zależność w równości ([[#1|1]]) przemnożonej przez <math>2 </math> , dostajemy: | Podstawiając tę zależność w równości ([[#1|1]]) przemnożonej przez <math>2</math> , dostajemy: | ||
| Linia 70: | Linia 70: | ||
Każdy wierzchołek leży na trzech ścianach. | Każdy wierzchołek leży na trzech ścianach. | ||
Z drugiej strony <math>x </math> ścian ma pięć wierzchołków, a <math>y </math> sześć. | Z drugiej strony <math>x</math> ścian ma pięć wierzchołków, a <math>y</math> sześć. | ||
Licząc więc pary <math>\left( v,f \right) </math> , gdzie wierzchołek <math>v </math> | Licząc więc pary <math>\left( v,f \right)</math> , gdzie wierzchołek <math>v</math> | ||
leży na ścianie <math>f </math> , dostajemy: | leży na ścianie <math>f</math> , dostajemy: | ||
| Linia 79: | Linia 79: | ||
Podstawiając tę zależność w równości ([[#2|2]]) przemnożonej przez <math>3 </math> , dostajemy: | Podstawiając tę zależność w równości ([[#2|2]]) przemnożonej przez <math>3</math> , dostajemy: | ||
| Linia 86: | Linia 86: | ||
Liczba ścian pięciokątnych wynosi więc <math>x=12 </math> . | Liczba ścian pięciokątnych wynosi więc <math>x=12</math> . | ||
</div></div> | </div></div> | ||
{{cwiczenie|3|cw 3| | {{cwiczenie|3|cw 3| | ||
Pokaż, że dla spójnego, prostego grafu planarnego <math>\mathbf{G}=\left( V,E \right) </math> o co najmniej trzech wierzchołkach zachodzi | Pokaż, że dla spójnego, prostego grafu planarnego <math>\mathbf{G}=\left( V,E \right)</math> o co najmniej trzech wierzchołkach zachodzi | ||
| Linia 104: | Linia 104: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Rozważmy dowolną płaską reprezentacje grafu <math>\mathbf{G} </math> . | Rozważmy dowolną płaską reprezentacje grafu <math>\mathbf{G}</math> . | ||
Ponieważ <math>\mathbf{G} </math> jest grafem prostym, to | Ponieważ <math>\mathbf{G}</math> jest grafem prostym, to | ||
dowolna ściana w tej reprezentacji jest ograniczona przez co najmniej trzy krawędzie. | dowolna ściana w tej reprezentacji jest ograniczona przez co najmniej trzy krawędzie. | ||
Z drugiej strony każda krawędź graniczy z co najwyżej dwiema ścianami. | Z drugiej strony każda krawędź graniczy z co najwyżej dwiema ścianami. | ||
Po przeliczeniu par <math>\left( e,w \right) </math> takich, że krawędź <math>e </math> ogranicza ścianę <math>w </math> , | Po przeliczeniu par <math>\left( e,w \right)</math> takich, że krawędź <math>e</math> ogranicza ścianę <math>w</math> , | ||
otrzymujemy nierówność | otrzymujemy nierówność | ||
| Linia 116: | Linia 116: | ||
gdzie <math>f </math> to liczba ścian w rozważanej płaskiej prezentacji. | gdzie <math>f</math> to liczba ścian w rozważanej płaskiej prezentacji. | ||
Po podstawieniu tej nierówności do wzoru z Twierdzenia [[Matematyka dyskretna 1/Wykład 14: Grafy III#tw_14.4|14.4]] otrzymujemy: | Po podstawieniu tej nierówności do wzoru z Twierdzenia [[Matematyka dyskretna 1/Wykład 14: Grafy III#tw_14.4|14.4]] otrzymujemy: | ||
| Linia 136: | Linia 136: | ||
{{cwiczenie|4|cw 4| | {{cwiczenie|4|cw 4| | ||
Pokaż, że spójny graf planarny <math>\mathbf{G} </math> | Pokaż, że spójny graf planarny <math>\mathbf{G}</math> | ||
o co najmniej jednym wierzchołku posiada wierzchołek | o co najmniej jednym wierzchołku posiada wierzchołek | ||
o stopniu nie większym niż <math>5 </math> . | o stopniu nie większym niż <math>5</math> . | ||
}} | }} | ||
| Linia 149: | Linia 149: | ||
Oczywiście taki wierzchołek musi istnieć w grafie z jednym bądź dwoma wierzchołkami. | Oczywiście taki wierzchołek musi istnieć w grafie z jednym bądź dwoma wierzchołkami. | ||
Bez straty ogólności możemy przyjąć, | Bez straty ogólności możemy przyjąć, | ||
że <math>\mathbf{G} </math> jest spójnym, płaskim grafem o co najmniej trzech wierzchołkach. | że <math>\mathbf{G}</math> jest spójnym, płaskim grafem o co najmniej trzech wierzchołkach. | ||
Załóżmy, że każdy wierzchołek <math>\mathbf{G} </math> ma stopień co najmniej sześć. | Załóżmy, że każdy wierzchołek <math>\mathbf{G}</math> ma stopień co najmniej sześć. | ||
Wtedy zależność między stopniami wierzchołków, a liczbą krawędzi daje: | Wtedy zależność między stopniami wierzchołków, a liczbą krawędzi daje: | ||
| Linia 169: | Linia 169: | ||
{{cwiczenie|5|cw 5| | {{cwiczenie|5|cw 5| | ||
Znajdź liczbę chromatyczną <math>{k} </math> -wymiarowej kostki <math>\mathcal{Q}_{k} </math> , czyli | Znajdź liczbę chromatyczną <math>{k}</math> -wymiarowej kostki <math>\mathcal{Q}_{k}</math> , czyli | ||
grafu, którego wierzchołki to ciągi <math>\left( a_1,a_2,\ldots,a_k \right) </math> , gdzie <math>a_i=0,1 </math> , | grafu, którego wierzchołki to ciągi <math>\left( a_1,a_2,\ldots,a_k \right)</math> , gdzie <math>a_i=0,1</math> , | ||
a krawędzie łączą te ciągi, które różnią się tylko na jednej pozycji. | a krawędzie łączą te ciągi, które różnią się tylko na jednej pozycji. | ||
| Linia 181: | Linia 181: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Podzielmy wierzchołki kostki <math>\mathcal{Q}_{k} </math> na dwa zbiory: | Podzielmy wierzchołki kostki <math>\mathcal{Q}_{k}</math> na dwa zbiory: | ||
* <math>V_1\subseteq \mathsf{ V}\!\left(\mathcal{Q}_{k}\right) </math> to zbiór wierzchołków o nieparzystej liczbie jedynek, | * <math>V_1\subseteq \mathsf{ V}\!\left(\mathcal{Q}_{k}\right)</math> to zbiór wierzchołków o nieparzystej liczbie jedynek, | ||
* <math>V_2\subseteq \mathsf{ V}\!\left(\mathcal{Q}_{k}\right) </math> to zbiór wierzchołków o parzystej liczbie jedynek, | * <math>V_2\subseteq \mathsf{ V}\!\left(\mathcal{Q}_{k}\right)</math> to zbiór wierzchołków o parzystej liczbie jedynek, | ||
W sąsiednich wierzchołkach liczba jedynek różni się o <math>1 </math> , | W sąsiednich wierzchołkach liczba jedynek różni się o <math>1</math> , | ||
w szczególności różni się parzystością. | w szczególności różni się parzystością. | ||
A zatem miedzy wierzchołkami z <math>V_i </math> nie ma krawędzi, | A zatem miedzy wierzchołkami z <math>V_i</math> nie ma krawędzi, | ||
czyli <math>\mathcal{Q}_{k}=\left( V_1\cup V_2, \mathsf{ E}\!\left(\mathcal{Q}_{k}\right) \right) </math> | czyli <math>\mathcal{Q}_{k}=\left( V_1\cup V_2, \mathsf{ E}\!\left(\mathcal{Q}_{k}\right) \right)</math> | ||
jest grafem dwudzielnym, czyli dwukolorowalnym. | jest grafem dwudzielnym, czyli dwukolorowalnym. | ||
</div></div> | </div></div> | ||
| Linia 206: | Linia 206: | ||
istnieje wierzchołek stopnia co najwyżej trzy. | istnieje wierzchołek stopnia co najwyżej trzy. | ||
Niech więc, dla dowodu niewprost, | Niech więc, dla dowodu niewprost, | ||
<math>graf{G} </math> będzie płaską prezentacją grafu bez trójkątów, | <math>graf{G}</math> będzie płaską prezentacją grafu bez trójkątów, | ||
w którym każdy wierzchołek ma stopień conajmniej cztery. | w którym każdy wierzchołek ma stopień conajmniej cztery. | ||
Z faktu, że każda krawędź ogranicza co najmniej dwie ściany, | Z faktu, że każda krawędź ogranicza co najmniej dwie ściany, | ||
| Linia 216: | Linia 216: | ||
gdzie <math>f </math> oznacza liczbę ścian w grafie <math>\mathbf{G} </math> . | gdzie <math>f</math> oznacza liczbę ścian w grafie <math>\mathbf{G}</math> . | ||
Korzystając z Twierdzenia [[Matematyka dyskretna 1/Wykład 14: Grafy III#tw_14.4|14.4]] otrzymujemy, że | Korzystając z Twierdzenia [[Matematyka dyskretna 1/Wykład 14: Grafy III#tw_14.4|14.4]] otrzymujemy, że | ||
| Linia 248: | Linia 248: | ||
Dowód trójkolorowalności planarnego grafu <math>\mathbf{G} </math> bez trójkątów | Dowód trójkolorowalności planarnego grafu <math>\mathbf{G}</math> bez trójkątów | ||
poprowadzimy teraz indukcyjnie ze względu na liczbę wierzchołków <math>n </math> tego grafu. | poprowadzimy teraz indukcyjnie ze względu na liczbę wierzchołków <math>n</math> tego grafu. | ||
Dla grafów o <math>n=1 </math> jest to oczywiste. | Dla grafów o <math>n=1</math> jest to oczywiste. | ||
Załóżmy, że <math>n\geq 2 </math> . | Załóżmy, że <math>n\geq 2</math> . | ||
Jak już wiemy, w planarnym grafie bez trójkątów | Jak już wiemy, w planarnym grafie bez trójkątów | ||
istnieje wierzchołek, powiedzmy <math>v </math> , o stopniu co najwyżej trzy. | istnieje wierzchołek, powiedzmy <math>v</math> , o stopniu co najwyżej trzy. | ||
Graf <math>\mathbf{G}-\left\lbrace v \right\rbrace </math> ma <math>n-1 </math> wierzchołków | Graf <math>\mathbf{G}-\left\lbrace v \right\rbrace</math> ma <math>n-1</math> wierzchołków | ||
więc, na mocy założenia indukcyjnego, można go pokolorować czterema kolorami. | więc, na mocy założenia indukcyjnego, można go pokolorować czterema kolorami. | ||
Wierzchołek <math>v </math> miał co najwyżej trzech sąsiadów, | Wierzchołek <math>v</math> miał co najwyżej trzech sąsiadów, | ||
więc musi istnieć kolor <math>c </math> nie wykorzystany przez sąsiadów <math>v </math> . | więc musi istnieć kolor <math>c</math> nie wykorzystany przez sąsiadów <math>v</math> . | ||
Wierzchołek <math>v </math> kolorujemy właśnie na kolor <math>c </math> . | Wierzchołek <math>v</math> kolorujemy właśnie na kolor <math>c</math> . | ||
Uzyskaliśmy w konsekwencji kolorowanie grafu <math>\mathbf{G} </math> za pomocą czterech barw, | Uzyskaliśmy w konsekwencji kolorowanie grafu <math>\mathbf{G}</math> za pomocą czterech barw, | ||
co kończy dowód. | co kończy dowód. | ||
</div></div> | </div></div> | ||
Wersja z 10:12, 5 wrz 2023
Grafy III
Ćwiczenie 1
Ćwiczenie 2
W pewnym wielościanie wszystkie ściany są pięciokątami i sześciokątami. Ile jest ścian pięciokątnych, jeżeli w każdym wierzchołku spotykają się dokładnie trzy ściany?
Ćwiczenie 3
Pokaż, że dla spójnego, prostego grafu planarnego o co najmniej trzech wierzchołkach zachodzi
Ćwiczenie 4
Pokaż, że spójny graf planarny o co najmniej jednym wierzchołku posiada wierzchołek o stopniu nie większym niż .
Ćwiczenie 5
Znajdź liczbę chromatyczną -wymiarowej kostki , czyli grafu, którego wierzchołki to ciągi , gdzie , a krawędzie łączą te ciągi, które różnią się tylko na jednej pozycji.
Ćwiczenie 6
Nie korzystając z Twierdzenia 14.13 o czterech barwach pokaż, że graf planarny bez trójkątów jest czterokolorowalny.