PF Moduł 11

Wykład

Wykład 11 - Pole elektryczne 11.1 Prawo Coulomba 11.2 Opis dynamiczny pola elektrycznego 11.3 Opis energetyczny pola elektrycznego 11.4 Ogólne własności pola elektrycznego wytworzonego przez ładunki 11.5 Dipol elektryczny 11.6 Własności elektryczne przewodników 11.7 Własności elektryczne izolatorów 11.8 Ruch ładunku w polu elektrycznym 11.9 Pojemność elektryczna 11.10 Opis procesów ładowania i rozładowania kondensatora 11.11 - 15 Materiały do ćwiczeń

---

11.1 Prawo Coulomba Dwa punktowe ładunki elektryczne Parser nie mógł rozpoznać (błąd składni): {\displaystyle q_1\} , i Parser nie mógł rozpoznać (błąd składni): {\displaystyle q_2\} , działają na siebie siłą, której wartość jest wprost proporcjonalna do iloczynu ładunków i odwrotnie proporcjonalna do kwadratu ich wzajemnej odległości: $\overrightarrow{F}=\frac{1}{4\pi {\epsilon }_0{\epsilon }_r}\cdot \frac{q_1{q}_2}{r^2}\cdot \frac{\overrightarrow{r}}{r}$ ${\epsilon }_0=8,85\cdot 10^{-12}\frac{C^2}{N{m}^2}$ gdzie Parser nie mógł rozpoznać (błąd składni): {\displaystyle \varepsilon_0\} , jest przenikalnością elektryczną próżni zaś Parser nie mógł rozpoznać (błąd składni): {\displaystyle \varepsilon_r\} , względną przenikalnością ośrodka. Ładunki różnoimienne przyciągają się, jednoimienne odpychają. Można udowodnić, że wzór ten określa również wartość siły, jaką działają na siebie jednorodne ładunki kuliste z odległości r większej od sumy ich promieni.

---

11.2 Opis dynamiczny pola elektrycznego Pole elektryczne wytworzone przez ładunki elektryczne to przestrzeń, w której na umieszczony ładunek działa siła elektryczna. Oddziaływaniu temu towarzyszy energia potencjalna zwana energią elektryczną. Opis pola elektrycznego powinien określać jego własności dynamiczne i energetyczne. Natężenie pola elektrycznego jest określone jako stosunek siły działającej w danym punkcie pola na punktowy ładunek próbny Parser nie mógł rozpoznać (błąd składni): {\displaystyle q_0\} , do wartości tego ładunku $\overrightarrow{F}=\frac{\overrightarrow{E}}{q_0}$ Wektor natężenia określa dynamiczne własności pola elektrycznego, co oznacza, że jeżeli znamy natężenie w danym punkcie pola, to siłę działającą na ładunek punktowy Parser nie mógł rozpoznać (błąd składni): {\displaystyle q\} , umieszczony w tym punkcie możemy obliczyć za pomocą wzoru $\overrightarrow{F}=q\cdot \overrightarrow{E}$ Linie sił pola elektrycznego to linie, do których styczny jest wektor siły, a więc i wektor natężenia pola. Zwrot linii sił pola jest określony przez zwrot wektora natężenia pola. Linie sił pola są w ogólności liniami krzywymi; w szczególnym przypadku, np. pola elektrycznego wytworzonego przez ładunek punktowy linie sił pola są liniami prostymi. Strumień wektora natężenia pola elektrycznego Porcję strumienia wektora natężenia pola elektrycznego przez mały element powierzchni dS (tak mały że może być traktowany jako płaski a natężenie pola w jego obrębie jest wektorem stałym) definiujemy jako: $d{\mathrm{\Phi }}_E=\overrightarrow{E}d\overrightarrow{S}=E\cdot S\cdot cos(\overrightarrow{E},d\overrightarrow{S})$ ${\mathrm{\Phi }}_E=\underset{S}{\int }\overrightarrow{E}d\overrightarrow{S}$ gdzie Parser nie mógł rozpoznać (błąd składni): {\displaystyle d\overrightarrow{S}\} , jest wektorem prostopadłym do tego elementu powierzchni, o wartości równej polu powierzchni Parser nie mógł rozpoznać (błąd składni): {\displaystyle dS\} ,. Wartość strumienia wektora natężenia pola elektrycznego przez całą powierzchnię Parser nie mógł rozpoznać (błąd składni): {\displaystyle S\} ,, którą obliczamy przez zsumowanie porcji strumienia przez poszczególne elementy powierzchni Parser nie mógł rozpoznać (błąd składni): {\displaystyle dS\} ,, jest równa liczbie linii sił pola przecinających tę powierzchnię. W najprostszym przypadku, gdy pole elektryczne jest jednorodne, strumień wektora natężenia pola elektrycznego przez płaszczyznę o powierzchni Parser nie mógł rozpoznać (błąd składni): {\displaystyle S\} , jest równy ${\mathrm{\Phi }}_E=EScos\alpha$ gdzie Parser nie mógł rozpoznać (błąd składni): {\displaystyle \alpha\} , jest kątem między wektorem natężenia pola elektrycznego i normalną do powierzchni. Prawo Gaussa dla wektora natężenia pola elektrycznego Strumień wektora natężenia pola elektrycznego przez zamkniętą powierzchnię ograniczającą układ ładunków wytwarzających pole elektryczne jest wprost proporcjonalny do sumarycznego ładunku układu Parser nie mógł rozpoznać (błąd składni): {\displaystyle Q\} , ${\mathrm{\Phi }}_E={\oint }_S\overrightarrow{E}d\overrightarrow{S}=\frac{1}{{\epsilon }_0{\epsilon }_r}Q$ $Q=\underset{V}{\int }\rho dV$ Współczynnik proporcjonalności jest tak dobrany, aby wyznaczony z prawa Gaussa wzór na natężenie pola elektrycznego wytworzonego przez ładunek punktowy Parser nie mógł rozpoznać (błąd składni): {\displaystyle Q\} , był zgodny ze wzorem wyznaczonym na podstawie prawa Coulomba. Prawo Gaussa wyraża bardzo ważną własność pola elektrycznego: jest to pole źródłowe. Źródłem pola jest ładunek. Ładunek dodatni jest dodatnim źródłem pola (linie sił pola wychodzą z ładunku dodatniego), ładunek ujemny jest ujemnym źródłem pola (linie sił pola wchodzą do ładunku ujemnego).

---

11.3 Opis energetyczny pola elektrycznego Praca Na ładunek punktowy q pole elektryczne o natężeniu Parser nie mógł rozpoznać (błąd składni): {\displaystyle \overrightarrow{E}\} , działa siłą $\overrightarrow{F}=q\cdot \overrightarrow{E}$ . Zatem praca przesunięcia ładunku z punktu Parser nie mógł rozpoznać (błąd składni): {\displaystyle A\} , do punktu Parser nie mógł rozpoznać (błąd składni): {\displaystyle B\} , jest określona wzorem: $W(A\to B)=-\underset{A}{\overset{B}{\int }}q\overrightarrow{E}d\overrightarrow{l}=q\underset{A}{\overset{B}{\int }}-\overrightarrow{E}d\overrightarrow{l}$ gdzie Parser nie mógł rozpoznać (błąd składni): {\displaystyle d\overrightarrow{l}\} , jest bardzo małym elementem krzywej wzdłuż której jest przesuwany ładunek. Można w prosty sposób wykazać, że wynik całkowania jest identyczny dla wszystkich krzywych łączących punkty Parser nie mógł rozpoznać (błąd składni): {\displaystyle A\} , i Parser nie mógł rozpoznać (błąd składni): {\displaystyle B\} ,. Oznacza to, że siła elektryczna jest siłą zachowawczą. Warto przypomnieć interpretację znaku pracy: praca dodatnia jest wykonana przez siły zewnętrzne, praca ujemna jest wykonana przez siły wewnętrzne, czyli przez układ fizyczny: pole - ładunek. Elektryczna energia potencjalna jest określona w następujący sposób: Wyobraźmy sobie przejście układu fizycznego oddziałującego siłami elektrycznymi od stanu fizycznego nr 1 do stanu fizycznego nr 2. Obydwu stanom przypisujemy elektryczną energię potencjalną, przy czym energia potencjalna układu w stanie drugim jest równa sumie energii potencjalnej w stanie pierwszym i pracy wykonanej przy przejściu od stanu do stanu $W_p(2)=W_p(1)+W(1\to 2)$ Praca wykonana przy przejściu od stanu nr 1 do stanu nr 2 spełnia w przypadku oddziaływań elektrycznych podstawowy warunek sensowności takiej definicji, tzn. jest niezależna od sposobu przejścia układu fizycznego od stanu początkowego do stanu końcowego (siły elektryczne są siłami zachowawczymi). Stan nr 1, czyli tzw. stan odniesienia można określić dwoma sposobami: Jako stan odniesienia wybieramy dowolny stan układu fizycznego i przypisujemy mu dowolną wartość energii (np. +100 J, -50 J, 0, ...); taki sposób jest często stosowany w zadaniach. Jako stan odniesienia wybieramy taki stan układu fizycznego, w którym siły elektryczne maleją do zera (odległość oddziałujących ładunków jest bardzo duża) i przypisujemy mu energię potencjalną równą zeru. Ten sposób określania energii potencjalnej jest często stosowany w teorii. Otrzymujemy wzory o charakterze ogólnym. Z takiego sposobu określania energii wynika, że energia potencjalna towarzysząca oddziaływaniom przyciągającym (ładunki różnoimienne) jest ujemna, zaś energia potencjalna towarzysząca oddziaływaniom odpychającym (ładunki jednoimienne) jest dodatnia. Potencjał elektryczny jest określony jako stosunek energii potencjalnej oddziaływania ładunku próbnego Parser nie mógł rozpoznać (błąd składni): {\displaystyle +q_0\} , z polem elektrycznym, w danym punkcie pola, do wartości tego ładunku $\phi =\frac{W_p}{+q_0}$ Potencjał elektryczny określa energetyczne własności pola elektrycznego, co oznacza, że jeżeli znamy potencjał w danym punkcie pola elektrycznego, to energię potencjalną oddziaływania pola z ładunkiem umieszczonym w tym punkcie możemy obliczyć ze wzoru $W_p=q\phi$ Ponieważ potencjał elektryczny jest określony za pomocą energii potencjalnej, to oczywiście ma on też charakter względny, a zatem potencjał elektryczny w danym punkcie pola jest równy sumie potencjału w punkcie odniesienia i pracy przeniesienia jednostkowego ładunku dodatniego z punktu odniesienia do danego punktu pola $\phi (2)=\phi (1)+\frac{W(1\to 2)}{+q_0}=\phi (1)-\underset{1}{\overset{2}{\int }}\overrightarrow{E}d\overrightarrow{l}$ przy czym słuszne pozostają uwagi dotyczące sposobu wyboru stanu odniesienia i wartości potencjału w tym stanie. Uwaga: W zadaniach, w których nie jest wyraźnie określony stan odniesienia i wartość potencjału w tym stanie, potencjał jest zwykle określany względem nieskończoności, gdzie przyjmujemy potencjał równy zeru. Powierzchnie ekwipotencjalne to powierzchnie, na których potencjał elektryczny ma stałą wartość. Powierzchnie ekwipotencjalne są prostopadłe do linii sił pola. Pracę przesunięcia ładunku punktowego Parser nie mógł rozpoznać (błąd składni): {\displaystyle q\} , w polu elektrycznym można wyrazić wzorem $W(1\to 2)=q[\phi (2)-\phi (1)]$

---

11.4 Ogólne własności pola elektrycznego wytworzonego przez ładunki Związek między natężeniem pola i potencjałem Natężenie pola i potencjał elektryczny zostały zdefiniowane w taki sposób, że zależą tylko od własności pola elektrycznego, które opisują, a nie od tego co w tym polu umieszczamy. Związek między wielkością wektorową, jaką jest natężenie pola, i wielkością skalarną, jaką jest potencjał, określono w następujący sposób: Jeżeli przesuwamy się wzdłuż linii sił pola, to wartość wektora natężenia pola jest równa szybkości zmiany potencjału, wziętej ze znakiem minus $E=-\frac{d\phi }{dr}$ gdzie dr jest bardzo małym przesunięciem. Minus oznacza, że zwrot wektora natężenia pola jest przeciwny do zwrotu przesunięcia przy którym potencjał rośnie. Linie sił pola są prostopadłe do powierzchni ekwipotencjalnych. Ogólny wzór określający związek między natężeniem pola i potencjałem można zapisać w postaci różniczkowej lub całkowej $\overrightarrow{E}=-grad\phi$ $\phi (2)=\phi (1)-\underset{1}{\overset{2}{\int }}\overrightarrow{E}d\overrightarrow{l}$ Ogólne własności: Pole elektryczne wytworzone przez ładunki to pole: źródłowe ${\oint }_S\overrightarrow{E}d\overrightarrow{S}=\frac{1}{{\epsilon }_0{\epsilon }_r}Q$ źródłem pola jest ładunek zachowawcze $W(A\to B)=-\underset{A}{\overset{B}{\int }}q\overrightarrow{E}d\overrightarrow{l}$ siła elektryczna jest siłą zachowawczą bezwirowe ${\oint }_L\overrightarrow{E}d\overrightarrow{l}=0$ linie sił pola mają początek i koniec, nie są krzywymi zamkniętymi

---

11.5 Dipol elektryczny Dipol elektryczny stanowią dwa ładunki różnoimienne Parser nie mógł rozpoznać (błąd składni): {\displaystyle +q\} , i Parser nie mógł rozpoznać (błąd składni): {\displaystyle -q\} , położone w odległości d. Układowi temu przypisujemy wektor elektrycznego momentu dipolowego określony wzorem ${\overrightarrow{p}}_e=q\overrightarrow{d}$ gdzie Parser nie mógł rozpoznać (błąd składni): {\displaystyle \overrightarrow{d}\} , jest wektorem skierowanym od ładunku ujemnego do dodatniego. Natężenie pola elektrycznego wytworzonego przez dipol w odległości Parser nie mógł rozpoznać (błąd składni): {\displaystyle r\} ,, dużej w porównaniu z ramieniem dipola Parser nie mógł rozpoznać (błąd składni): {\displaystyle d\} ,, ma wartość określoną wzorem $E=\frac{p_e}{r^3}$ W zewnętrznym polu elektrycznym na dipol działa moment sił określony wzorem $\overrightarrow{M}={\overrightarrow{p}}_e\times \overrightarrow{E}$ Energia potencjalna oddziaływania dipola z zewnętrznym polem elektrycznym względem stanu, w którym ${\overrightarrow{p}}_e\perp \overrightarrow{E}$, wynosi $W_p=-{\overrightarrow{p}}_e\cdot \overrightarrow{E}$ Wartości momentu sił działającego na dipol i energii oddziaływania z zewnętrznym polem zestawiono w tabeli dla różnych wartości kąta Parser nie mógł rozpoznać (błąd składni): {\displaystyle \alpha\} , jaki tworzy wektor momentu dipolowego z wektorem natężenia zewnętrznego pola. kąt Parser nie mógł rozpoznać (błąd składni): {\displaystyle \alpha\} , Parser nie mógł rozpoznać (błąd składni): {\displaystyle 0\} , Parser nie mógł rozpoznać (błąd składni): {\displaystyle 90^\circ\} , Parser nie mógł rozpoznać (błąd składni): {\displaystyle 180^\circ\} , Parser nie mógł rozpoznać (błąd składni): {\displaystyle 270^\circ\} , moment sił Parser nie mógł rozpoznać (błąd składni): {\displaystyle M\} , Parser nie mógł rozpoznać (błąd składni): {\displaystyle 0\} , Parser nie mógł rozpoznać (błąd składni): {\displaystyle pE\} , Parser nie mógł rozpoznać (błąd składni): {\displaystyle 0\} , Parser nie mógł rozpoznać (błąd składni): {\displaystyle -pE\} , energia potencjalna Parser nie mógł rozpoznać (błąd składni): {\displaystyle W_p\} , Parser nie mógł rozpoznać (błąd składni): {\displaystyle -pE\} , minimum Parser nie mógł rozpoznać (błąd składni): {\displaystyle 0\} , Parser nie mógł rozpoznać (błąd składni): {\displaystyle +pE\} , maksimum Parser nie mógł rozpoznać (błąd składni): {\displaystyle 0\} , stan równowagi trwała - nietrwała - Z zestawienia tego wynika, że oddziaływanie z zewnętrznym polem elektrycznym dąży do ustawienia dipola tak, aby wektor momentu dipolowego był zgodny z wektorem natężenia pola, czyli w stanie równowagi trwałej.

---

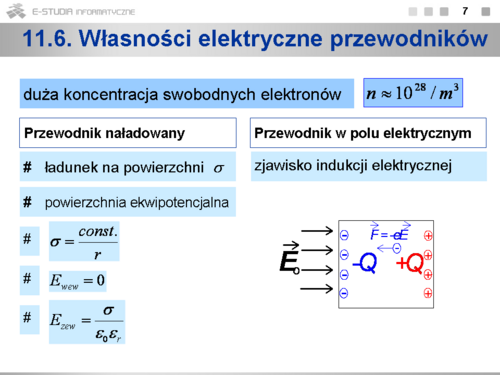11.6 Własności elektryczne przewodników Przewodniki to ciała stałe o dużej koncentracji swobodnych elektronów (rzędu koncentracji atomów). Sumaryczny ładunek nienaładowanego przewodnika jest równy zero. Przewodnik naładowany W stanie równowagi ładunek gromadzi się na powierzchni przewodnika (swobodne ładunki jednoimienne w objętości przewodnika odpychają się i przemieszczają dotąd, dopóki nie znajdą się na powierzchni). W stanie równowagi powierzchnia naładowanego przewodnika jest powierzchnią ekwipotencjalną (ładunki przemieszczają się po powierzchni dopóty, dopóki potencjały wszystkich punktów nie wyrównają się, gdyby potencjały w dowolnych dwóch punktach były różne, następowałby między nimi przepływ ładunku). Rozkład gęstości powierzchniowej ładunku Parser nie mógł rozpoznać (błąd składni): {\displaystyle \sigma\} , jest zależny od kształtu przewodnika, gęstość powierzchniowa jest tym większa im mniejszy jest lokalny promień krzywizny powierzchni przewodnika. Natężenie pola elektrycznego wewnątrz przewodnika jest równe zeru (wynika to z prawa Gaussa). Natężenie pola elektrycznego na zewnątrz przewodnika, w pobliżu jego powierzchni jest wektorem prostopadłym do powierzchni i ma wartość $E=\frac{\sigma }{{\epsilon }_0}$ co wynika z prawa Gaussa. Przewodnik w polu elektrycznym Pod wpływem zewnętrznego pola elektrycznego zachodzi w przewodniku zjawisko indukcji elektrycznej, które polega na przemieszczeniu elektronów swobodnych tak, aby pole elektryczne wytworzone przez nowy rozkład elektronów skompensowało całkowicie wnikające pole zewnętrzne (wypadkowe pole wewnątrz przewodnika pozostaje równe zeru). W wyniku zjawiska indukcji elektrycznej przewodnik jako całość pozostaje obojętny, ale jego poszczególne części uzyskują ładunki przeciwnych znaków o jednakowej wartości.

---

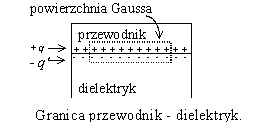
11.7 Własności elektryczne izolatorów Izolatory, czyli dielektryki to substancje, w których koncentracja swobodnych elektronów jest bardzo mała, a o własnościach elektrycznych decydują ładunki związane, które mogą wykonywać tylko niewielkie ruchy wokół położeń równowagi. W obojętnym dielektryku zewnętrzne pole elektryczne powoduje polaryzację dielektryczną - niewielkie przesunięcia ładunków związanych, których skutkiem jest uzyskanie przez każdy element objętości pewnego momentu dipolowego. Pola elektryczne ładunków wewnątrz dielektryka znoszą się. Przesunięcia ładunków w warstwach przypowierzchniowych powodują, że na przeciwległych powierzchniach prostopadłych do wektora natężenia pola indukują się ładunki powierzchniowe Parser nie mógł rozpoznać (błąd składni): {\displaystyle q'\} , o przeciwnych znakach. Pole w dielektryku jest sumą pola wnikającego i przeciwnego pola pochodzącego od ładunków powierzchniowych, którego natężenie jest zawsze mniejsze od natężenia pola zewnętrznego. Zatem natężenie pola w dielektryku jest różne od zera (przeciwnie niż w przewodniku), ale mniejsze od natężenia pola zewnętrznego. Stosunek wartości wektorów: natężenia pola zewnętrznego Parser nie mógł rozpoznać (błąd składni): {\displaystyle E_0\} , i natężenia pola w dielektryku Parser nie mógł rozpoznać (błąd składni): {\displaystyle E\} , jest względną przenikalnością elektryczną dielektryka Parser nie mógł rozpoznać (błąd składni): {\displaystyle \varepsilon_r\} , $\frac{E_0}{E}={\epsilon }_r$ Analiza sytuacji na granicy przewodnik - dielektryk. Weźmy izolowany przewodnik, na powierzchni którego znajduje się ładunek +q. Pod nieobecność dielektryka prawo Gaussa na granicy przewodnik - próżnia (dla zamkniętej powierzchni, której przekrój przedstawiono na rysunku linią przerywaną) ma postać $E_{0}S=\frac{1}{{\epsilon }_0}q$ gdzie Parser nie mógł rozpoznać (błąd składni): {\displaystyle S\} , jest polem przekroju powierzchni Gaussa równoległym do płaszczyzny przewodnika. Po wprowadzeniu jednorodnego, izotropowego dielektryka prawo Gaussa dla tej samej zamkniętej powierzchni przyjmie postać $E_{0}S=\frac{1}{{\epsilon }_0}(q-q^{\prime })$ co oznacza, że strumień wektora natężenia pola pochodzi zarówno od ładunków swobodnych (na powierzchni przewodnika) jak i od ładunków związanych (na powierzchni dielektryka). Za pomocą powyższych równań można obliczyć związany ładunek Parser nie mógł rozpoznać (błąd składni): {\displaystyle q'\} , zaindukowany na powierzchni dielektryka $q^{\prime }=q(1-\frac{1}{{\epsilon }_r})$ który jest mniejszy od ładunku na powierzchni przewodnika. Po podstawieniu Parser nie mógł rozpoznać (błąd składni): {\displaystyle q'\} , równanie przyjmie postać ${\epsilon }_0{\epsilon }_{r}ES=q$ Lewą stronę tego równania można potraktować jako całkowity strumień przez zamkniętą powierzchnię Gaussa pewnego wektora ${\epsilon }_0{\epsilon }_r\overrightarrow{E}=\overrightarrow{D}$ zwanego wektorem indukcji elektrycznej. Przez analogię do strumienia wektora Parser nie mógł rozpoznać (błąd składni): {\displaystyle \overrightarrow{E}\} , , strumień wektora Parser nie mógł rozpoznać (błąd składni): {\displaystyle \overrightarrow{D}\} , jest określony jako iloczyn skalarny $d{\mathrm{\Phi }}_D=\overrightarrow{D}\cdot d\overrightarrow{S}$ Prawo Gaussa dla wektora Parser nie mógł rozpoznać (błąd składni): {\displaystyle \overrightarrow{D}\} , Strumień wektora Parser nie mógł rozpoznać (błąd składni): {\displaystyle \overrightarrow{D}\} , przez zamkniętą powierzchnię ograniczającą układ ładunków wytwarzających pole elektryczne jest wprost proporcjonalny do sumarycznego ładunku swobodnego układu Parser nie mógł rozpoznać (błąd składni): {\displaystyle q\} , ${\oint }_S\overrightarrow{D}\cdot d\overrightarrow{S}=q$ Taka postać prawa Gaussa oznacza, że strumień wektora Parser nie mógł rozpoznać (błąd składni): {\displaystyle \overrightarrow{D}\} , pochodzi tylko od ładunków swobodnych (na powierzchni przewodnika). Z porównania wzorów wynika, że wprowadzenie wektora indukcji umożliwia nam pominięcie po prawej stronie prawa Gaussa kłopotliwego ładunku indukowanego w dielektryku i uwzględnienie jego wpływu na natężenie pola w dielektryku poprzez wprowadzenie po lewej stronie równania względnej przenikalności elektrycznej Parser nie mógł rozpoznać (błąd składni): {\displaystyle \varepsilon_r\} ,. Istotna różnica między wektorami Parser nie mógł rozpoznać (błąd składni): {\displaystyle \overrightarrow{E}\} , i Parser nie mógł rozpoznać (błąd składni): {\displaystyle \overrightarrow{D}\} , polega również na tym, że na granicy przewodnika z dielektrykiem występuje skok wartości wektora natężenia pola, natomiast wartość wektora indukcji zmienia się w sposób ciągły. Należy dodać, że podany powyżej związek między wektorem natężenia pola i wektorem indukcji elektrycznej jest słuszny dla dielektryków izotropowych; istnieją dielektryki dla których związek ten staje się bardziej skomplikowany.

---

11.8 Ruch ładunku w polu elektrycznym Na ładunek punktowy Parser nie mógł rozpoznać (błąd składni): {\displaystyle q\} , pole elektryczne o natężeniu Parser nie mógł rozpoznać (błąd składni): {\displaystyle \overrightarrow{E}\} , działa siłą Parser nie mógł rozpoznać (błąd składni): {\displaystyle \overrightarrow{F}=q\cdot \overrightarrow{E}\} , . Skutkiem działania siły jest zmiana prędkości oraz energii kinetycznej. Rozważmy typowe przypadki: Pole jednorodne. Siła ma stałą wartość, kierunek i zwrot. Pod wpływem takiej siły ładunek może się poruszać ruchem jednostajnie zmiennym prostoliniowo (wzdłuż linii sił pola) lub po paraboli, w zależności od orientacji wektora prędkości początkowej. Pole wytworzone przez ładunek punktowy. W tym przypadku siła jest siłą centralną, przyciągającą lub odpychającą. Można udowodnić, że w polu siły centralnej ładunek może się poruszać po krzywych stożkowych: hiperboli, paraboli, elipsie lub okręgu, w zależności od wartości i orientacji wektora prędkości początkowej (por. ruch masy w polu grawitacyjnym). Oczywiście w przypadku siły odpychającej niemożliwe są tory zamknięte.

---

11.9 Pojemność elektryczna Stosunek ładunku wprowadzonego na przewodnik do potencjału wytworzonego na jego powierzchni jest dla danego przewodnika wielkością stałą. Wielkość tę, określającą zdolność przewodnika do gromadzenia ładunku nazywamy pojemnością elektryczną $C=\frac{Q}{\phi }$ Pojemność elektryczna przewodnika zależy od: kształtu i rozmiarów przewodnika, własności elektrycznych ośrodka w którym znajduje się przewodnik oraz od obecności w pobliżu przewodnika innych przewodników. Przewodnik lub układ przewodników służący do gromadzenia ładunku nazywamy kondensatorem. W przypadku gdy kondensator składa się z dwóch przewodników, we wzorze określającym pojemność potencjał zastępujemy różnicą potencjałów Parser nie mógł rozpoznać (błąd składni): {\displaystyle U\} ,. Pojemność elektryczną typowych kondensatorów możemy obliczyć korzystając z definicji. Energia naładowanego kondensatora Energia zgromadzona w kondensatorze czyli energia pola elektrycznego jest równa pracy wykonanej podczas ładowania kondensatora $W_E=\frac{1}{2}QU=\frac{Q^2}{2C}=\frac{1}{2}C{U}^2$ Gęstość energii pola elektrycznego w kondensatorze, czyli energia przypadająca na jednostkę objętości wyraża się wzorem $w_B=\frac{1}{2}{\epsilon }_0{\epsilon }_r{E}^2=\frac{1}{2}\overrightarrow{E}\cdot \overrightarrow{D}$

---

11.10 Opis procesów ładowania i rozładowania kondensatora Ładowanie kondensatora W chwili początkowej $t_0=0$ kondensator dołączamy do źródła stałego napięcia Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_0\} ,. Zależność od czasu ładunku na kondensatorze, napięcia i natężenia prądu jest opisana przez funkcję eksponencjalną, charakterystyczną dla procesów samorzutnych. O szybkości osiągania maksymalnej wartości ładunku Parser nie mógł rozpoznać (błąd składni): {\displaystyle Q_m\} ,, osiągania napięcia Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_0\} , oraz zaniku prądu ładowania kondensatora decyduje stała czasowa tego procesu Parser nie mógł rozpoznać (błąd składni): {\displaystyle \tau\} , , zależna od pojemności kondensatora oraz oporności obwodu. $Q(t)=Q_m(1-e^{-t/\tau })$ $U(t)=U_0(1-e^{-t/\tau })$ $I(t)=I_0{e}^{-t/\tau }$ $\tau =RC$ Funkcje te otrzymujemy rozwiązując równanie opisujące stan obwodu w chwili Parser nie mógł rozpoznać (błąd składni): {\displaystyle t\} ,: $U_0-R\frac{dQ}{dt}-\frac{Q}{C}=0$ Rozładowanie kondensatora W chwili początkowej $t_0=0$ do okładek kondensatora naładowanego ładunkiem Parser nie mógł rozpoznać (błąd składni): {\displaystyle Q_0\} , dołączamy opornik o oporności Parser nie mógł rozpoznać (błąd składni): {\displaystyle R\} ,. Zależność od czasu ładunku na kondensatorze, napięcia i natężenia prądu jest również opisana przez funkcję eksponencjalną. charakterystyczną dla procesów samorzutnych. O szybkości zaniku ładunku, napięcia oraz prądu rozładowania kondensatora decyduje również stała czasowa tego procesu Parser nie mógł rozpoznać (błąd składni): {\displaystyle \tau\} , , zależna od pojemności kondensatora oraz oporności opornika. $Q(t)=Q_0{e}^{-t/\tau }$ $U(t)=U_0{e}^{-t/\tau }$ $I(t)=I_0{e}^{-t/\tau }$ $\tau =RC$ Funkcje te otrzymujemy rozwiązując równanie opisujące stan obwodu w chwili Parser nie mógł rozpoznać (błąd składni): {\displaystyle t\} ,: $-R\frac{dQ}{dt}-\frac{Q}{C}=0$

---

Materiały do ćwiczeń

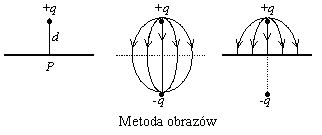
11.11 Materiały do ćwiczeń Metody obliczania wektora natężenia pola i potencjału Pole elektryczne może być wytworzone przez różne układy ładunków punktowych lub przez ładunek rozłożony w sposób ciągły w pewnym obszarze. W przypadku gdy pole elektryczne jest wytwarzone przez układ ładunków punktowych, natężenie pola w wybranym punkcie przestrzeni obliczamy jako wektorową sumę natężeń pól wytwarzanych przez poszczególne ładunki, zaś potencjał elektryczny jako skalarną sumę potencjałów. Korzystamy przy tym ze wzorów : $\overrightarrow{E}={\overrightarrow{E}}_1+{\overrightarrow{E}}_2+{\overrightarrow{E}}_3+\cdots$ $E_i=\frac{Q_i}{4\pi {\epsilon }_0{\epsilon }_r{r}^2}$ $\phi ={\phi }_1+{\phi }_2+{\phi }_3+\cdots$ $\phi =\frac{Q_i}{4\pi {\epsilon }_0{\epsilon }_{r}r}$ W celu obliczenia sumy wektorów wygodne może być wprowadzenie układu współrzędnych i zsumowanie odpowiednich współrzędnych wektorów. Potencjał obliczony w powyższy sposób będzie oczywiście potencjałem względem nieskończoności. Korzystając z definicji można taki potencjał przeliczyć względem dowolnego innego punktu odniesienia. W przypadku gdy pole elektryczne jest wytwarzone przez ładunek rozłożony w sposób ciągły w pewnym obszarze, do obliczania wektora natężenia pola stosujemy metodę Gaussa lub tzw. metodę superpozycji. Metoda Gaussa wykorzystuje prawo Gaussa. W tym celu należy ładunek wytwarzający pole otoczyć zamkniętą powierzchnią przechodzącą przez punkt, w którym chcemy obliczyć natężenie pola. Kształt tej powierzchni powinien być taki, żeby obliczenie strumienia wektora natężenia pola elektrycznego przez tę powierzchnię było łatwe, tzn. żeby w każdym punkcie tej powierzchni wartość wektora natężenia była taka sama oraz żeby kąt, jaki tworzy wektor natężenia z wektorem prostopadłym do powierzchni, miał stałą wartość Parser nie mógł rozpoznać (błąd składni): {\displaystyle \alpha\} ,. Taką własność ma zwykle powierzchnia o takiej samej symetrii co pole, a ta z kolei wynika z symetrii ładunku wytwarzającego pole. Wtedy strumień wektora natężenia pola elektrycznego przez tę powierzchnię jest równy ${\mathrm{\Phi }}_E=EScos\alpha$ Należy jeszcze obliczyć ładunek Parser nie mógł rozpoznać (błąd składni): {\displaystyle Q\} , ograniczony powierzchnią Gaussa. Ładunek może być rozłożony w sposób ciągły na pewnej krzywej, powierzchni lub w pewnej objętości. Używamy w takich przypadkach odpowiedniej gęstości ładunku: liniowej Parser nie mógł rozpoznać (błąd składni): {\displaystyle \lambda [C/m]\} ,, powierzchniowej Parser nie mógł rozpoznać (błąd składni): {\displaystyle \sigma [C/m2]\} , lub objętościowej Parser nie mógł rozpoznać (błąd składni): {\displaystyle \rho [C/cm3]\} ,, która jest ilością ładunku w jednostkowym elemencie danego obszaru. Ładunek Parser nie mógł rozpoznać (błąd składni): {\displaystyle Q\} , jest sumą ładunku rozłożonego w obszarze otoczonym powierzchnią Gaussa. Po podstawieniu do wzoru $EScos\alpha =\frac{1}{{\epsilon }_0{\epsilon }_r}Q$ $Q=\underset{V}{\int }\rho dV$ można obliczyć wartość natężenia pola elektrycznego Parser nie mógł rozpoznać (błąd składni): {\displaystyle E\} ,. Znając natężenie pola można obliczyć potencjał, korzystając ze wzoru wyrażającego związek między potencjałem i natężeniem pola, z uwzględnieniem warunku jaki ma spełniać potencjał w stanie odniesienia. Prawo Gaussa jest oczywiście słuszne dla dowolnego układu ładunków lecz metoda wykorzystująca to prawo daje się zastosować praktycznie tylko w przypadku pola o wyrażnej symetrii (np. kulistej, cylindrycznej). Metoda superpozycji stosowana jest w takich przypadkach, gdy nie można zastosować metody Gaussa. Ładunek rozłożony w sposób ciągły w pewnym obszarze dzielimy na bardzo małe porcje ładunku Parser nie mógł rozpoznać (błąd składni): {\displaystyle dQ\} ,, tak małe aby mogły być uznane za ładunki punktowe. Natężenie pola w wybranym punkcie przestrzeni obliczamy jako wektorową sumę natężeń pól wytwarzanych przez poszczególne porcje ładunku $dE=\frac{dQ}{4\pi {\epsilon }_0{\epsilon }_r{r}^2}$ gdzie Parser nie mógł rozpoznać (błąd składni): {\displaystyle r\} , jest odległością od danej porcji ładunku do punktu, w którym obliczamy natężenie pola. Zwykle wprowadzamy układ współrzędnych i sumujemy odpowiednie składowe wektorów Parser nie mógł rozpoznać (błąd składni): {\displaystyle d\overrightarrow{E}\} ,. Znając natężenie pola można obliczyć potencjał, korzystając ze wzoru wyrażającego związek między potencjałem i natężeniem pola, z uwzględnieniem warunku jaki ma spełniać potencjał w stanie odniesienia. Można też obliczyć potencjał w tym punkcie, jako sumę potencjałów pól wytworzonych przez poszczególne porcje ładunku $\phi =\int \frac{dQ}{4\pi {\epsilon }_0{\epsilon }_{r}r}$ Potencjał obliczony w ten sposób będzie oczywiście potencjałem względem nieskończoności. Korzystając z definicji można taki potencjał przeliczyć względem dowolnego innego punktu odniesienia. Metoda obrazów. W sytuacjach, w których mamy do czynienia ze zjawiskiem indukcji elektrycznej, powstają zwykle skomplikowane rozkłady ładunków zaindukowanych. Metoda obrazów polega na tym, aby bardziej skomplikowany układ ładunków zastąpić prostszym układem wytwarzającym takie samo pole elektryczne. Układem takim jest zwykle układ ładunków punktowych zwanych ładunkami obrazowymi. Ideę metody można przedstawić w najprostszym przypadku układu składającego się z punktowego ładunku dodatniego Parser nie mógł rozpoznać (błąd składni): {\displaystyle +q\} , położonego w odległosci Parser nie mógł rozpoznać (błąd składni): {\displaystyle d\} , od przewodzącej płaszczyzny. Ładunek ten indukuje w przewodzącej płaszczyźnie ładunek ujemny którego gęstość powierzchniowa jest funkcją odległości od punktu P. Powierzchnia przewodząca jest powierzchnią ekwipotencjalną. Układ taki można zastąpić układem dwóch ładunków punktowych: Parser nie mógł rozpoznać (błąd składni): {\displaystyle +q\} , i jego obrazem o przeciwnym znaku Parser nie mógł rozpoznać (błąd składni): {\displaystyle -q\} ,, położonym symetrycznie względem płaszczyzny. Dla takiego układu ładunków miejsce geometryczne, w którym była przewodząca płaszczyzna, będzie również powierzchnią ekwipotencjalną. Fikcyjny ładunek-obraz wytwarza w górnej półprzestrzeni takie pole elektryczne, jak ładunki zaindukowane na przewodzącej płaszczyźnie.

---

11.12. Materiały do ćwiczeń Przykładowe pola elektryczne Pole elektryczne jednorodne Jest to pole w którym natężenie pola Parser nie mógł rozpoznać (błąd składni): {\displaystyle \overrightarrow{E}\} , jest wektorem stałym, tzn. w każdym punkcie pola ma taką samą wartość, kierunek i zwrot. Linie sił pola jednorodnego są zbiorem prostych równoległych. Powierzchnie ekwipotencjalne są zbiorem równoległych płaszczyzn. Pole elektryczne wytworzone przez ładunek punktowy Natężenie pola elektrycznego $\overrightarrow{E}(r)=\frac{Q}{4\pi {\epsilon }_0{\epsilon }_r{r}^2}\cdot \frac{\overrightarrow{r}}{r}$ Potencjał elektryczny względem nieskończoności $\phi (r)=\frac{Q}{4\pi {\epsilon }_0{\epsilon }_{r}r}$ Siła jaką pole działa na punktowy ładunek Parser nie mógł rozpoznać (błąd składni): {\displaystyle q\} , $\overrightarrow{F}=q\overrightarrow{E}=\frac{qQ}{4\pi {\epsilon }_0{\epsilon }_r{r}^2}\cdot \frac{\overrightarrow{r}}{r}$ Energia potencjalna oddziaływania pola z punktowym ładunkiem Parser nie mógł rozpoznać (błąd składni): {\displaystyle q\} , $W_p(r)=q\phi (r)=\frac{qQ}{4\pi {\epsilon }_0{\epsilon }_{r}r}$ Praca przesunięcia punktowego ładunku Parser nie mógł rozpoznać (błąd składni): {\displaystyle q\} , w polu punktowego ładunku Parser nie mógł rozpoznać (błąd składni): {\displaystyle Q\} , $W(r_1\to r_2)=q[\phi (r_2)-\phi (r_1)]=\frac{qQ}{4\pi {\epsilon }_0{\epsilon }_r}(\frac{1}{r_1}-\frac{1}{r_2})$ Pole wytworzone przez jednorodnie naładowaną dielektryczną kulę Kula o promieniu Parser nie mógł rozpoznać (błąd składni): {\displaystyle R\} , i gęstości objętościowej ładunku Parser nie mógł rozpoznać (błąd składni): {\displaystyle \rho\} , ładunek całkowity :$Q=\frac{4}{3}\pi R^3\rho$ Natężenie pola elektrycznego (obliczone za pomocą metody Gaussa) $\begin{array}{cc}r>R:& E=\frac{\rho R^3}{3{\epsilon }_0{r}^2}=\frac{Q}{4\pi {\epsilon }_0{r}^2}\end{array}$ $\begin{array}{cc}r<R:& E=\frac{\rho }{3{\epsilon }_0{\epsilon }_r}r\end{array}$ (uwaga: zależność liniowa) Potencjał (względem Parser nie mógł rozpoznać (błąd składni): {\displaystyle \infty\} , ) $\begin{array}{cc}r>R:& E=\frac{\rho R^3}{3{\epsilon }_{0}r}=\frac{Q}{4\pi {\epsilon }_{0}r}\end{array}$ $\begin{array}{cc}r<R:& \phi =\frac{\rho }{3{\epsilon }_0{\epsilon }_r}\cdot \frac{3R^2-r^2}{2}=\frac{Q}{4\pi {\epsilon }_{0}R}\cdot \frac{3R^2-r^2}{2R^2}\end{array}$ (uwaga: zależność kwadratowa) Potencjał na powierzchni i w środku kuli $\phi (R)=\frac{\rho R^2}{3{\epsilon }_0}=\frac{Q}{4\pi {\epsilon }_{0}R}$ $\phi (0)=\frac{3}{2}\phi (R)$ Pole wytworzone przez naładowaną płaszczyznę Pole elektryczne wytworzone przez bardzo dużą płaszczyznę naładowaną równomiernie z gęstością powierzchniową łądunku Parser nie mógł rozpoznać (błąd składni): {\displaystyle \sigma\} , jest polem jednorodnym, którego linie sił są prostopadłe do płaszczyzny zaś natężenie jest określone wzorem $E=\frac{\sigma }{2{\epsilon }_0}$ Wzór ten można łatwo otrzymać za pomocą metody Gaussa.

---

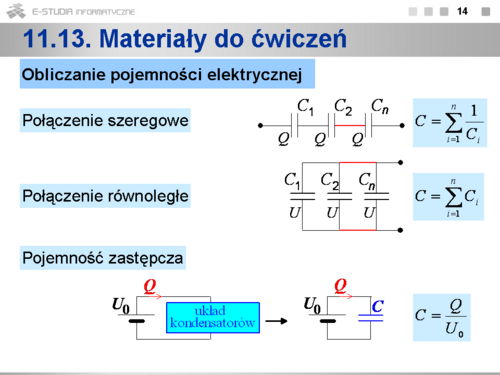
11.13. Materiały do ćwiczeń Obliczanie pojemności elektrycznej kondensatorów Spośród różnych możliwych połączeń kondensatorów wyróżniamy dwa podstawowe - połączenie szeregowe i połączenie równoległe. Kondensatory uznajemy za układ połączony szeregowo, jeżeli ładunki na tych kondensatorach są jednakowe. W takim układzie kondensatorów ładunek jest dostarczany z zewnątrz tylko do okładek zewnętrznych; ładunki na okładkach wewnętrznych powstają wskutek zjawiska indukcji elektrycznej. Pojemność elektryczną układu kondensatorów połączonych szeregowo obliczamy za pomocą wzoru $\frac{1}{C}=\sum _i\frac{1}{C_i}$ Kondensatory uznajemy za układ połączony równolegle, jeżeli napięcia na tych kondensatorach są jednakowe. W takim układzie kondensatorów ładunek jest dostarczany z zewnątrz do każdego kondensatora. Pojemność elektryczną układu kondensatorów połączonych równolegle obliczamy ze wzoru $C=\sum _i{C}_i$ Układy kondensatorów spotykane w zadaniach są często zagmatwane. Aby obliczyć pojemność takiego układu, staramy się narysować go w prostszy sposób, ustalając które kondensatory są połączone szeregowo a które równolegle. Układ kondensatorów można oczywiście przekształcać tylko w taki sposób, aby rozkład ładunków na kondensatorach nie uległ zmianie. Najczęściej stosowane są dwa sposoby: punkty o tym samym potencjale można połączyć, pojedynczy kondensator można zastąpić dwoma kondensatorami, które następnie można rozłączyć. Przy analizie połączeń kondensatorów należy zwracać uwagę na symetrię układu, która ułatwia np. dostrzeżenie punktów o tym samym potencjale. Są też oczywiście układy kondensatorów, które nie są połączone ani szeregowo, ani równolegle. Korzystając z definicji można obliczyć pojemność elektryczną dowolnego kondensatora lub układu kondensatorów. Należy obliczyć ładunek jaki dopłynie do kondensatora (układu kondensatorów) po podłączeniu do źródła ustalonego napięcia. Ładunek ten będzie proporcjonalny do napięcia, a współczynnik proporcjonalności to pojemność kondensatora (układu kondensatorów) $Q=C\cdot U_0$. Do obliczania ładunku Parser nie mógł rozpoznać (błąd składni): {\displaystyle Q\} , wykorzystywane są dwa podstawowe prawa fizyczne: zasada zachowania ładunku, w polu elektrycznym suma zmian potencjału na drodze zamkniętej jest równa zeru. Za pomocą tej metody można obliczyć pojemność dowolnego układu kondensatorów, bez konieczności ustalania jak są połączone kondensatory, a więc nawet bez znajomości wzorów na łączenie szeregowe, równoległe, łączenia w trójkąt i w gwiazdę, ...

---

---

Zadania

1. Walec z dielektryka Parser nie mógł rozpoznać (błąd składni): {\displaystyle (\varphi_r)\} , o promieniu Parser nie mógł rozpoznać (błąd składni): {\displaystyle R\} , został naładowany z gęstością objętościową Parser nie mógł rozpoznać (błąd składni): {\displaystyle \rho\} ,. Znaleźć zależność natężenia, indukcji i potencjału pola elektrycznego od odległości Parser nie mógł rozpoznać (błąd składni): {\displaystyle r\} , od osi walca w następujących przypadkach:

a. $\rho =const$.

b. gęstość ładunku zależy od odległości Parser nie mógł rozpoznać (błąd składni): {\displaystyle r\} , od osi walca $\rho ={\rho }_0(r/R)$

W przypadku potencjału rozważyć następujące przypadki:

i) potencjał jest równy zeru w nieskończoności,

ii) potencjał na powierzchni walca jest równy ${\phi }_0$.

---

2. Cienki pręt został naładowany ze stałą gęstością liniową Parser nie mógł rozpoznać (błąd składni): {\displaystyle \lambda\} ,. Znaleźć natężenie pola elektrycznego w punkcie Parser nie mógł rozpoznać (błąd składni): {\displaystyle P\} , położonym w odległości Parser nie mógł rozpoznać (błąd składni): {\displaystyle a\} , od pręta. Punkt Parser nie mógł rozpoznać (błąd składni): {\displaystyle P\} , widać z końców pręta pod kątami Parser nie mógł rozpoznać (błąd składni): {\displaystyle \alpha\} , i Parser nie mógł rozpoznać (błąd składni): {\displaystyle \beta\} ,.

---

3. Punktowy ładunek Parser nie mógł rozpoznać (błąd składni): {\displaystyle q\} , umieszczono w odległości Parser nie mógł rozpoznać (błąd składni): {\displaystyle d\} , od środka przewodzącej kuli o promieniu Parser nie mógł rozpoznać (błąd składni): {\displaystyle R\} ,, naładowanej ładunkiem Parser nie mógł rozpoznać (błąd składni): {\displaystyle -Q\} ,. Obliczyć potencjał na powierzchni kuli oraz siłę działającą na ładunek Parser nie mógł rozpoznać (błąd składni): {\displaystyle q\} ,.

---

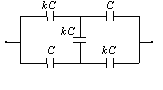
4. Obliczyć pojemność układu pięciu kondensatorów przedstawionego na rysunku. Pojemności kondensatorów wynoszą Parser nie mógł rozpoznać (błąd składni): {\displaystyle C\} , i Parser nie mógł rozpoznać (błąd składni): {\displaystyle kC\} ,, gdzie Parser nie mógł rozpoznać (błąd składni): {\displaystyle k\in R_{+}\} , . Przedyskutować zależność pojemności układu od parametru Parser nie mógł rozpoznać (błąd składni): {\displaystyle k\} ,.

---

5. Wnętrze sferycznego kondensatora kulistego o promieniach Parser nie mógł rozpoznać (błąd składni): {\displaystyle R_1\} , i Parser nie mógł rozpoznać (błąd składni): {\displaystyle R_2\} , wypełnione jest dielektrykiem. Względna przenikalność elektryczna wynosi Parser nie mógł rozpoznać (błąd składni): {\displaystyle \varepsilon_1\} , obszarze Parser nie mógł rozpoznać (błąd składni): {\displaystyle r\in (R_1,R)\} , oraz Parser nie mógł rozpoznać (błąd składni): {\displaystyle \varepsilon_2\} , w obszarze Parser nie mógł rozpoznać (błąd składni): {\displaystyle r\in (R,R_2)\} , , gdzie Parser nie mógł rozpoznać (błąd składni): {\displaystyle r\} , oznacza odległość od środka kondensatora. Znaleźć pojemność kondensatora. Obliczyć wartości gęstości powierzchniowej ładunku na powierzchniach o promieniach Parser nie mógł rozpoznać (błąd składni): {\displaystyle R_1\} , , Parser nie mógł rozpoznać (błąd składni): {\displaystyle R\} , i Parser nie mógł rozpoznać (błąd składni): {\displaystyle R_2\} , , gdy kula wewnętrzna jest naładowana ładunkiem Parser nie mógł rozpoznać (błąd składni): {\displaystyle Q\} ,.

---

Słowa kluczowe

Prawo Coulomba

Pole elektryczne

Natężenie pola elektrycznego

Linie sił pola elektrycznego

Strumień wektora natężenia

Prawo Gaussa

Praca

Energia potencjalna

Potencjał elektryczny

Powierzchnie ekwipotencjalne

Pole źródłowe

Pole zachowawcze

Pole bezwirowe

Pole jednorodne

Dipol elektryczny

Elektryczny moment dipolowy

Zjawisko indukcji elektrycznej

Wektor indukcji elektrycznej

Pojemność elektryczna

Gęstość energii pola elektrycznego

Stała czasowa ładowania kondensatora

Metoda superpozycji

Metoda obrazów

---