CWGI Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „,</math>” na „</math>,” |
m Zastępowanie tekstu – „ \</math>” na „</math>” |
||
| Linia 32: | Linia 32: | ||
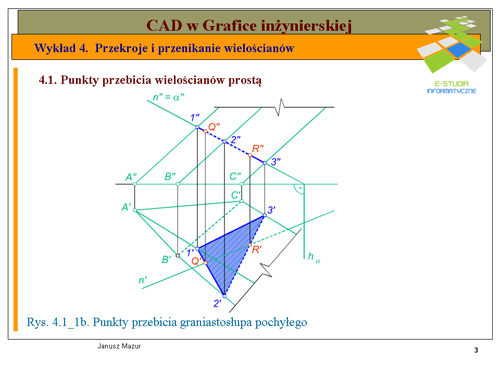
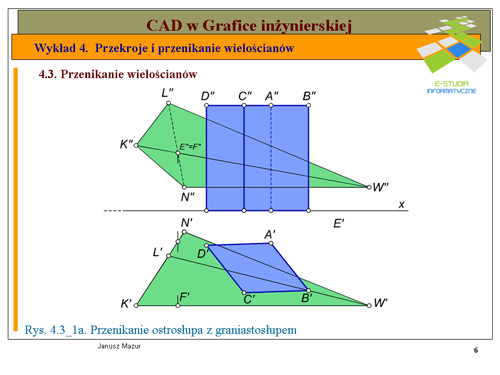
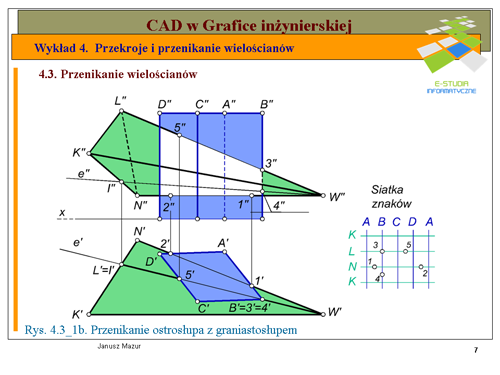
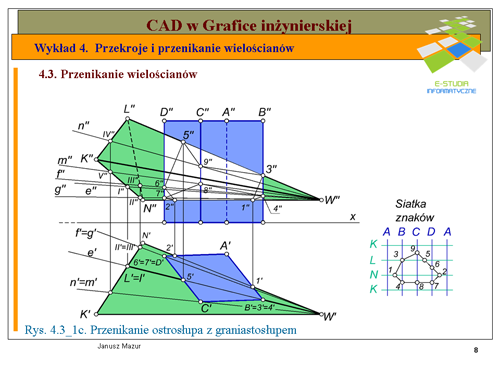
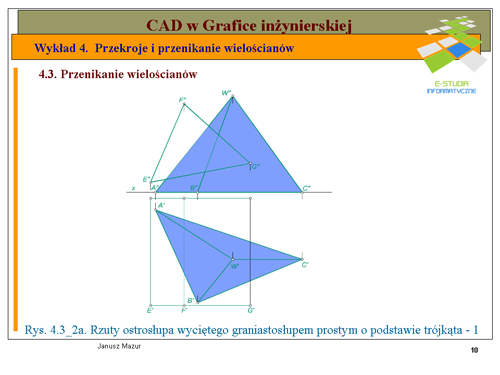
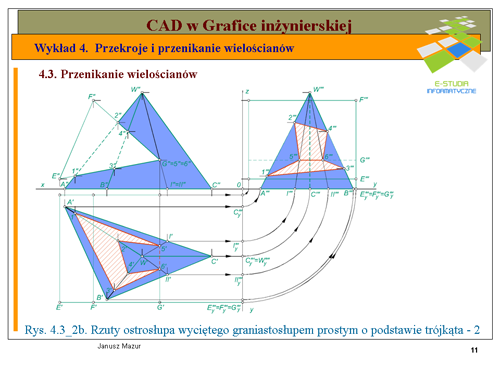
Pierwszym etapem rozwiązania zadania jest wyznaczenie rzutów przekroju graniastosłupa płaszczyzn, w której znajduje się dana prosta <math>n\</math>,. W tym celu przez prostą <math>n\</math>, prowadzimy dowolna płaszczyznę. Dla ułatwienia będzie to płaszczyzna pionowo – rzutująca <math>\alpha\</math>,, prostopadła do rzutni pionowej. Ślad pionowy płaszczyzny <math>v_\alpha</math> będzie pokrywał się z rzutem pionowym prostej <math>n\</math>,, ponieważ wszystkie elementy płaskie znajdujące się w takiej płaszczyźnie w rzucie pionowym rzutują się na ślad pionowy płaszczyzny, będący jednocześnie rzutem pionowym płaszczyzny. Kolejnym etapem rozwiązania jest wyznaczenie przekroju graniastosłupa płaszczyzną <math>\alpha\</math>,. Przekrój w rzucie pionowym wyznaczymy natychmiast. Zgodnie z cytowaną wyżej zasadą punkty przekroju <math>1", 2", 3"</math> w rzucie pionowym będą leżały na przecięciu się krawędzi graniastosłupa <math>A",B", C"</math> ze śladem pionowym płaszczyzny <math>\alpha\</math>,. Rzuty poziome punktów przekroju <math>1', 2', 3'</math> będą leżały na przecięciu się odnoszących z rzutami poziomymi krawędzi graniastosłupa <math>A', B', C'</math>. W miejscach gdzie prosta n przecina się z bokami przekroju otrzymamy poszukiwane punkty przebicia graniastosłupa prostą <math>n\</math>,. | Pierwszym etapem rozwiązania zadania jest wyznaczenie rzutów przekroju graniastosłupa płaszczyzn, w której znajduje się dana prosta <math>n\</math>,. W tym celu przez prostą <math>n\</math>, prowadzimy dowolna płaszczyznę. Dla ułatwienia będzie to płaszczyzna pionowo – rzutująca <math>\alpha\</math>,, prostopadła do rzutni pionowej. Ślad pionowy płaszczyzny <math>v_\alpha</math> będzie pokrywał się z rzutem pionowym prostej <math>n\</math>,, ponieważ wszystkie elementy płaskie znajdujące się w takiej płaszczyźnie w rzucie pionowym rzutują się na ślad pionowy płaszczyzny, będący jednocześnie rzutem pionowym płaszczyzny. Kolejnym etapem rozwiązania jest wyznaczenie przekroju graniastosłupa płaszczyzną <math>\alpha\</math>,. Przekrój w rzucie pionowym wyznaczymy natychmiast. Zgodnie z cytowaną wyżej zasadą punkty przekroju <math>1", 2", 3"</math> w rzucie pionowym będą leżały na przecięciu się krawędzi graniastosłupa <math>A",B", C"</math> ze śladem pionowym płaszczyzny <math>\alpha\</math>,. Rzuty poziome punktów przekroju <math>1', 2', 3'</math> będą leżały na przecięciu się odnoszących z rzutami poziomymi krawędzi graniastosłupa <math>A', B', C'</math>. W miejscach gdzie prosta n przecina się z bokami przekroju otrzymamy poszukiwane punkty przebicia graniastosłupa prostą <math>n\</math>,. | ||
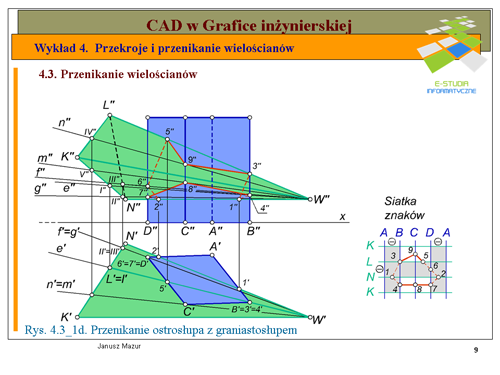
Dla pełnego rozwiązania zadania należy ustalić widoczność prostej, która wbija się w ściany graniastosłupa. W rzucie pionowym punkty przebicia znajdują się na ścianach widocznych, zatem prosta <math>n\</math>, będzie niewidoczna jedynie na odcinku między punktami przebicia. W rzycie poziomym jeden z punktów przebicia (punkt <math>Q' | Dla pełnego rozwiązania zadania należy ustalić widoczność prostej, która wbija się w ściany graniastosłupa. W rzucie pionowym punkty przebicia znajdują się na ścianach widocznych, zatem prosta <math>n\</math>, będzie niewidoczna jedynie na odcinku między punktami przebicia. W rzycie poziomym jeden z punktów przebicia (punkt <math>Q'</math>,) leży na ścianie niewidocznej <math>B’ C’</math>, więc prosta <math>n\</math>, będzie niewidoczna nie tylko między punktami przebicia ale również do miejsca wyjścia prostej z raniastosłupa. Niewidoczne krawędzie zaznaczono odpowiednio linią kreskową. | ||
|} | |} | ||
Wersja z 09:56, 5 wrz 2023

|
Wykład 4. Przekroje i przenikanie wielościanów |

|