Języki, automaty i obliczenia/Ćwiczenia 8: Dalsze algorytmy dla języków regularnych. Problemy rozstrzygalne: Różnice pomiędzy wersjami

Wersja z 09:21, 5 wrz 2023

Ćwiczenie 1

Zastosuj algorytm Automat2GReg do automatu o następującej funkcji przejść:

\begin{array}{ccccc} f & s_{0} & s_{1} & s_{2} & s_{3} \\ a & s_{1} & s_{2} & s_{0} & s_{2} \\ b & s_{3} & s_{2} & s_{2} & s_{2} \end{array}

gdzie $s_{0}$ jest stanem początkowym oraz $T = {s_{0}, s_{2}}$ .

Rozwiązanie

Pętla w liniach 7.--17. do zbioru $P$ doda następujące produkcje: $v_{0} \to a v_{1}$ , $v_{0} \to b v_{3}$ , $v_{1} \to a v_{2}$ , $v_{1} \to b v_{2}$ , $v_{2} \to a v_{0}$ , $v_{2} \to b v_{2}$ , $v_{3} \to a v_{2}$ , $v_{3} \to b v_{2}$ . Ponieważ stanami końcowymi są $s_{0}$ i $s_{2}$ , w pętli (w liniach 12.--14.) dodane zostaną jeszcze produkcje $v_{0} \to 1$ oraz $v_{2} \to 1$ .

Ćwiczenie 2

Zbuduj automaty akceptujące języki generowane następującymi gramatykami ( $v_{i}$ oznaczają symbole nieterminalne, $a, b$ -- terminalne):

1. $v_{0} \to a v_{0}$ , $v_{0} \to b v_{1}$ , $v_{0} \to b v_{2}$ , $v_{1} \to b v_{0}$ , $v_{1} \to a v_{2}$ , $v_{2} \to a v_{0}$ , $v_{2} \to 1$ .

2. $v_{0} \to a v_{1}$ , $v_{0} \to b$ , $v_{1} \to b v_{0}$ , $v_{1} \to a v_{1}$ , $v_{1} \to 1$ .

Rozwiązanie punktu 1

Postępując zgodnie z algorytmem GReg2Automat, obliczamy funkcję przejść tworzonego automatu (w tym przypadku niedeterministycznego) o stanach $s_{0}, s_{1}, s_{2}$ (stanem początkowym jest $s_{0}$ ):

$f (s_{0}, a) = {f_{0}}$ , $f (s_{0}, b) = {s_{1}, s_{2}}$ , $f (s_{1}, b) = {s_{0}, s_{2}}$ , $f (s_{2}, a) = s_{0}$ . Ponieważ w gramatyce istnieje produkcja $v_{2} \to 1$ , stan $s_{2}$ oznaczamy jako końcowy.

Rozwiązanie punktu 2

Ponieważ w gramatyce występuje produkcja $v_{0} \to b$ , która ma postać niezgodną z postacią produkcji będących wejściem algorytmu, przekształcamy gramatykę, usuwając tę produkcję i dodając dwie inne: $v_{0} \to b v_{k}$ oraz $v_{k} \to 1$ . Teraz możemy skonstruować automat. Jego zbiór stanów to $s_{0}, s_{1}, s_{k}$ , stanem początkowym jest $s_{0}$ , a funkcja przejść zdefiniowana jest następująco:

$f (s_{0}, a) = s_{1}$ , $f (s_{0}, b) = s_{k}$ , $f (s_{1}, a) = s_{1}$ , $s (s_{1}, b) = s_{0}$ .

Ponieważ w gramatyce wystąpiły produkcje $v_{1} \to 1$ oraz $v_{k} \to 1$ , stany $v_{1}$ oraz $v_{k}$ są stanami końcowymi.

W wykładzie podany został algorytm Automat2WR1 budujący wyrażenie regularne na podstawie zadanego automatu. Opiszemy teraz inną metodę rozwiązania tego problemu, wykorzystującą równania na językach.

Dany niech będzie automat $𝒜 = (S, A, f, s_{0}, T)$ . Chcemy zbudować wyrażenie regularne opisujące język akceptowany przez $𝒜$ . Do wyprowadzenia metody potrzebować będziemy lematu Ardena.

Lemat 0.1. [Arden]

Niech

R \subseteq A^{+}

i

S \subseteq A^{*}

będą językami regularnymi. Wtedy równanie

X = X R + S

posiada jedyne rozwiązanie $X = S R^{*}$ , które jest językiem regularnym.

Zdefiniujmy najpierw $L_{i}$ jako język tych słów, które byłyby

akceptowane przez

𝒜

, gdyby stanem końcowym był stan

s_{i}

, tzn. gdyby

T = {s_{i}}

:

L_{i} = {w \in A^{*} : f (s_{0}, w) = s_{i}}

.

Zauważmy, że jeśli do stanu $s_{t}$ wchodzą strzałki prowadzące ze stanów $s_{i_{1}}, s_{i_{2}}, . . ., s_{i_{n}}$ odpowiednio z etykietami $a_{1}, a_{2}, . . ., a_{n}$ (i tylko takie), to

L_{t} = \sum_{j = 1}^{n} L_{i_{j}} a_{j}

.

Obserwacja ta jest podstawą do konstrukcji metody otrzymywania wyrażenia regularnego na podstawie automatu. Będziemy budować układ równań, w którym każde równanie będzie postaci $L_{i} = \sum_{j \in I} L_{j} a_{j}$ , $I = {i_{1}, i_{2}, . . ., i_{n}}$ , gdzie $L_{i}$ traktowane są jak niewiadome. Następnie układ taki rozwiążemy ze względu na każdą zmienną $L_{i}$ (tu pomocny będzie lemat Ardena). Szukanym przez nas wyrażeniem regularnym będzie wyrażenie postaci $\sum_{i \in I} L_{i}$ , gdzie $I$ jest zbiorem indeksów $i$ stanów końcowych $s_{i}$ automatu $𝒜$ .

Można postawić w tym momencie pytanie, czy budowany układ równań ma rozwiązanie, a jeśli tak, to czy jest ono jedyne. Okazuje się że w rozważanej przez nas sytuacji ma to miejsce, choć dowód tego faktu nie jest natychmiastowy. Fakt ten, podobnie jak lemat Ardena, podajemy tutaj bez dowodu.

Algorytm Automat2WR2 - buduje inną metodą wyrażenie regularne opisujące język akceptowany przez automat skończony

  1  Wejście:  $𝒜 = (S, A, f, s_{0}, T)$  - automat akceptujący język  $L$ .
  2  Wyjście:  $r$  -- wyrażenie regularne opisujące język  $L$ .
  3  for each  $s \in S$  
  4    for each  $t \in S$  
  5      for each   $a \in A$ 
  6         $L_{s} \leftarrow$ "";                                 $▹$  wyrażenie puste
  7        if  $f (t, a) = s$  
  8          if  $L_{s} =$ ""
  9             $L_{s} \leftarrow L_{t} a$ ;            $▹$  podstawiamy wyrażenie regularne
 10          else
 11             $L_{s} \leftarrow L_{s} + L_{t} a$ ;       $▹$  podstawiamy wyrażenie regularne
 12          end if
 13        end if
 14      end for
 15    end for
 16    if  $s = s_{0}$   and   $s \in T$  then
 17       $L_{s} \leftarrow L_{s} + 1$ ;               $▹$  podstawiamy wyrażenie regularne
 18    end if
 19  end for
 20  rozwiąż  ${L_{i} = \sum_{t \in S} L_{t}}_{i = 0, . . ., | S | - 1}$ ;
 21   $r \leftarrow \sum_{s_{i} \in T} L_{i}$ ;
 22  return  $r$ ;

Funkcja rozwiąż w algorytmie Automat2Wr2 rozwiązuje układ równań (mający na podstawie wcześniejszych uwag jednoznaczne rozwiązania), zwraca obliczone języki $L_{i}$ , $i = 0, . . ., | S | - 1$ .

Rozwiązanie można wykonać metodą rugowania, przechodząc od $L_{n}$ do $L_{1}$ . Równanie $L_{i} = \sum_{t \in S} L_{t}$ rozwiązujemy, korzystając ze wzoru w lemacie Ardena (rolę $X$ w lemacie odgrywa $L_{i}$ ) i podstawiamy do pozostałych równań (tzn. równań dla $i = 0, \dots, i - 1$ ). Mając już wyliczone $L_{0}$ , wyliczamy kolejne $L_{i}$ idąc od $1$ do $| S | - 1$ . Dla lepszego zrozumienia metody przedstawiamy następujący przykład.

Przykład 1.1.

Dany niech będzie automat pokazany na rysunku 1 (pominęliśmy tu dla uproszczenia jedną strzałkę wychodzącą ze stanu $s_{2}$ w celu uniknięcia zwiększenia liczby stanów, gdyż chcąc formalnie narysować automat deterministyczny, musielibyśmy dodać stan $s_{3}$ i zdefiniować $f (s_{2}, a) = s_{3}$ , $f (s_{3}, a) = f (s_{3}, b) = s_{3}$ , ale widać, że wcale nie trzeba wtedy obliczać języka $L_{3}$ , gdyż z tego stanu nie da się już wyjść - jest to tzw. sink state).

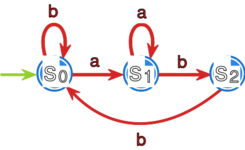
Ułóżmy równania do naszego układu równań. Mamy:

${\begin{cases} L_{0} = L_{0} b + L_{2} b + 1 \\ L_{1} = L_{0} a + L_{1} a \\ L_{2} = L_{1} b \end{cases} \Leftrightarrow {\begin{cases} L_{0} = L_{0} b + L_{1} b b + 1 \\ L_{1} = L_{0} a + L_{1} a \end{cases} \Leftrightarrow L_{0} = L_{0} b + L_{0} a a^{*} b b^{*} + 1$

Mamy więc $L_{0} = L_{0} (b + a^{+} b b) + 1$ . Korzystając z lematu Ardena, otrzymujemy $L_{0} = 1 (b + a^{+} b b)^{*} = (b + a^{+} b b)^{*}$ . Podstawiając obliczone $L_{0}$ do równania i obliczając pozostałe $L_{i}$ , otrzymujemy ostatecznie:

{\begin{cases} L_{0} = (b + a^{+} b b)^{*} \\ L_{1} = (b + a^{+} b b)^{*} a^{+} \\ L_{2} = (b + a^{+} b b)^{*} a^{+} b . \end{cases}

Ponieważ $T = {s_{0}, s_{1}, s_{2}}$ , rozwiązaniem jest:

w = L_{0} + L_{1} + L_{2} = (b + a^{+} b b)^{*} (1 + a^{+} (1 + b))

.

Ćwiczenie 3

Niech dany będzie automat $𝒜 (S = {s_{0}, s_{1}, s_{2}, s_{3}}, A = {a, b}, f, s_{0}, T = {s_{0}})$ o następującej funkcji przejść:

\begin{array}{ccccc} f & s_{0} & s_{1} & s_{2} & s_{3} \\ a & s_{1} & s_{2} & s_{0} & s_{3} \\ b & s_{3} & s_{2} & s_{2} & s_{3} \end{array}

Wykorzystując algorytm Automat2WR2, wyznacz wyrażenie regularne odpowiadające językowi akceptowanemu przez $𝒜$ .

Rozwiązanie

Po pierwsze zauważmy, że w obliczeniach nie musimy uwzględniać stanu $s_{3}$ ani języka $L_{3}$ stowarzyszonego z tym stanem. Układ równań będzie więc posiadał 3 równania o 3 niewiadomych $L_{0}$ , $L_{1}$ oraz $L_{2}$ :

{\begin{cases} L_{0} = L_{2} a + 1 \\ L_{1} = L_{0} a \\ L_{2} = L_{1} (a + b) + L_{2} b \end{cases}

W równaniu drugim zamieniamy $L_{0}$ na $L_{2} a + 1$ i otrzymujemy

{\begin{cases} L_{1} = (L_{2} a + 1) a = L_{2} a^{2} + a \\ L_{2} = L_{1} (a + b) + L_{2} b . \end{cases}

Teraz

L_{1}

w równaniu drugim zastępujemy prawą stroną równania pierwszego:

L_{2} = L_{1} (a + b) + L_{2} b = (L_{2} a^{2} + a) (a + b) + L_{2} b = L_{2} (a^{3} + a^{2} b + b) + a^{2} + a b

.

Korzystamy z lematu Ardena i otrzymujemy $L_{2} = (a^{2} + a b) (a^{3} + a^{2} b + b)^{*}$ . Podstawiamy to do równania $L_{0} = L_{2} a + 1$ i otrzymujemy ostatecznie:

L_{0} = (a^{2} + a b) (a^{3} + a^{2} b + b)^{*} a + 1 = (a^{2} + a b) (a^{2} (a + b) + b)^{*} a + 1

.

Można pokazać, że wyrażenie to jest równoważne następującemu:

L_{0} = (a (a + b) b^{*} a)^{*}

.

Ćwiczenie 4

Dane niech będą automaty: $n_{A}$ -stanowy $𝒜$ i $n_{B}$ -stanowy $ℬ$ , oba nad alfabetem $A$ i akceptujące odpowiednio języki $L (𝒜)$ i $L (ℬ)$ . Pokaż, że problem stwierdzenia, czy dla dowolnego $w \in A^{*}$ zachodzi $w \in L (𝒜) \cap L (ℬ)$ , jest rozstrzygalny:

poprzez skonstruowanie niedeterministycznego automatu posiadającego $O (n_{A} + n_{B})$ stanów,
poprzez skonstruowanie deterministycznego automatu $n_{A} \cdot n_{B}$ -stanowego.

Rozwiązanie punktu 1

Niech $𝒜 = (S_{A}, A, f_{A}, s_{A}^{0}, T_{A})$ oraz $ℬ = (S_{B}, A, f_{B}, s_{B}^{0}, T_{B})$ będą zadanymi automatami. Konstruujemy automat $𝒞 = (S, A, f, s_{0}, T)$ taki, że $S = S_{A} \cup S_{B} ∖ {s_{B}^{0}}$ , $s_{0} = s_{A}^{0}$ , $T = T_{B}$ , gdy $s_{B}^{0} \in̸ T_{B}$ , $T = T_{B} \cup T_{A}$ , gdy $s_{B}^{0} \in T_{B}$ , a funkcja przejść $f$ jest zdefiniowana następująco:

\begin{aligned} \forall s \in S_{A}, a \in A f (s, a) & = f_{A} (s, a) \\ \forall s \in S_{B} ∖ {s_{B}^{0}}, a \in A f (s, a) & = f_{B} (s, a) \\ \forall s \in T_{A}, a \in A f (s, a) & = f (s_{B}^{0}, a) . \end{aligned}

Zbiór stanów końcowych automatu $𝒜$ staje się więc zbiorem stanów początkowych dla automatu $ℬ$ , przy czym, jeśli $s_{B}^{0} \in T_{B}$ , to każdy ze stanów $T_{A}$ jest równocześnie stanem końcowym w automacie $𝒞$ . Zauważ, że:

w \in L (𝒜) \cap L (ℬ) ⟺ w w \in L (𝒞) \land f (s_{0}, w) \cap T_{A} = \emptyset

.

Oba warunki występujące po prawej stronie równoważności są algorytmicznie weryfikowalne i da się je sprawdzić w czasie $O (| w |)$ . Konstrukcja automatu $𝒞$ w oczywisty sposób również jest algorytmizowalna i da się ją wykonać w czasie $O (| A | (n_{A} + n_{B}))$ . Ponieważ $| S | = n_{A} + n_{B} - 1$ , więc $𝒞$ posiada $O (n_{A} + n_{B})$ stanów.

Rozwiązanie punktu 2

Ćwiczenie 5

Skonstruuj algorytm (oraz określ jego złożoność) dla następującego problemu (tym samym dowodząc jego rozstrzygalności):

Dany jest automat $𝒜 = (S, A, f, s_{0}, T)$ . Czy $L (𝒜) = \emptyset$ ?

Rozwiązanie

Bez straty ogólności możemy założyć, że automat jest deterministyczny. W algorytmie wykorzystamy procedurę Zaznacz przedstawioną poniżej.

Algorytm wykonuje przeszukanie automatu metodą DFS. Jego złożoność jest więc $O (| A | \cdot | S |)$ - liniowa ze względu na ilość stanów automatu. Złożoność pamięciowa także wynosi $O (| A | \cdot | S |)$ .

Algorytm PustośćJęzyka - sprawdza, czy język akceptowany przez zadany automat jest pusty

 1  Wejście:  $𝒜 = (S, A, f, s_{0}, T)$  - deterministyczny automat akceptujący język  $L$ .
 2  Wyjście: Odpowiedź true (tak) lub false (nie).
 3  ZAZNACZ $(s_{0})$ ;
 4  for each  $s \in T$  
 5    if  $zaznaczone [s] = 1$  
 6      return false
 7    end if
 8  end for
 9  return true;

 1  procedure Zaznacz( $s \in S$ )
 2   $zaznaczone [s] \leftarrow 1$ ;
 3  for each   $a \in A$  
 4    if zaznaczone $[f (s, a)] \neq 1$  
 5      ZAZNACZ $(f (s, a))$ ;
 6    end if
 7  end for
 8  end procedure

ZADANIA DOMOWE

Ćwiczenie 6

Zastosuj algorytm Automat2GReg do automatu o następującej funkcji przejść:

\begin{array}{ccccc} f & s_{0} & s_{1} & s_{2} & s_{3} \\ a & s_{1} & s_{3} & s_{3} & s_{3} \\ b & s_{2} & s_{2} & s_{0} & s_{0} \end{array}

gdzie $s_{0}$ jest stanem początkowym oraz $T = {s_{1}}$ .

Ćwiczenie 7

Zbuduj automaty akceptujące języki generowane następującymi gramatykami ( $v_{i}$ oznaczają symbole nieterminalne, $a, b$ -- terminalne):

1. $v_{0} \to a v_{1}$ , $v_{0} \to b v_{2}$ , $v_{0} \to b v_{0}$ , $v_{1} \to b v_{1}$ , $v_{1} \to a v_{0}$ , $v_{2} \to b v_{0}$ , $v_{2} \to b v_{2}$ , $v_{2} \to 1$ .

2. $v_{0} \to b v_{2}$ , $v_{0} \to b$ , $v_{1} \to b v_{0}$ , $v_{1} \to a v_{1}$ , $v_{1} \to 1$ , $v_{2} \to a v_{1}$ .

Ćwiczenie 8

Zbuduj automaty (z pustymi przejściami) akceptujące poniższe języki:

$b ((a + b)^{*} + a)$ ,
$(a + b)^{*} (a^{*} b^{*})$ ,
$a (b^{*} a^{*})^{*} + 1$ .

Wskazówka

Ćwiczenie 9

Niech dany będzie automat $𝒜 (S = {s_{0}, s_{1}, s_{2}, s_{3}}, A = {a, b}, f, s_{0}, T = {s_{0}})$ o następującej funkcji przejść:

\begin{array}{ccccc} f & s_{0} & s_{1} & s_{2} & s_{3} \\ a & s_{1} & s_{2} & s_{0} & s_{2} \\ b & s_{3} & s_{2} & s_{2} & s_{2} \end{array}

Wykorzystując algorytm Automat2WR2, wyznacz wyrażenie regularne odpowiadające językowi akceptowanemu przez $𝒜$ .

Ćwiczenie 10

Skonstruuj algorytmy dla następujących problemów rozstrzygalnych:

Równoważność dowolnych automatów $𝒜$ i $ℬ$ .
Nieskończoność języka $L (𝒜)$ dla dowolnego automatu $𝒜$ .

Wskazówka do punktu 1

Metoda pierwsza: istnieje dokładnie jeden automat minimalny. Metoda druga: rozważ automat akceptujący przecięcie $L (𝒜) \cap L (ℬ)$ tak jak w punkcie (2) zadania 4. punkt 2. Jaki warunek muszą spełniać stany $s \in S_{A}, t \in S_{B}$ , aby $(s, t) \in T$ ?

Wskazówka do punktu 2

1. Automat akceptuje nieskończenie wiele słów, gdy w wyrażeniu regularnym odpowiadającym temu automatowi występuje gwiazdka Kleene'ego. Użyj metody z twierdzenia Kleene'ego (Twierdzenie 1.1, punkt 5.).

2. $\exists s \in S, w_{1}, w_{2} \in A^{*} : f (s_{0}, w_{1}) = s \land f (s, w_{2}) = s . .$ .

@@ Linia 81: / Linia 81: @@
 Zdefiniujmy najpierw <math>L_i</math> jako język tych słów, które byłyby
-akceptowane przez <math>\mathcal{A}</math>, gdyby stanem końcowym był stan <math>s_i</math>, tzn. gdyby <math>T=\{s_i\}</math>: <center><math>L_i=\{w \in A^*:\ f(s_0,w)=s_i\}.</math></center>
+akceptowane przez <math>\mathcal{A}</math>, gdyby stanem końcowym był stan <math>s_i</math>, tzn. gdyby <math>T=\{s_i\}</math>: <center><math>L_i=\{w \in A^*:\ f(s_0,w)=s_i\}</math>.</center>
 Zauważmy, że jeśli do stanu <math>s_t</math> wchodzą strzałki prowadzące ze
 stanów <math>s_{i_1}, s_{i_2}, ..., s_{i_n}</math> odpowiednio z etykietami
 <math>a_1, a_2,..., a_n</math> (i tylko takie), to
-<center><math>L_t=\sum_{j=1}^n L_{i_j}a_j.</math></center>
+<center><math>L_t=\sum_{j=1}^n L_{i_j}a_j</math>.</center>
 Obserwacja ta jest podstawą do konstrukcji metody otrzymywania
@@ Linia 178: / Linia 178: @@
 Ponieważ <math>T=\{s_0,s_1,s_2\}</math>, rozwiązaniem jest:
-<center><math>w=L_0+L_1+L_2=(b+a^+bb)^*(1 + a^+(1 + b)).</math></center>
+<center><math>w=L_0+L_1+L_2=(b+a^+bb)^*(1 + a^+(1 + b))</math>.</center>
 {{cwiczenie|3||
@@ Linia 216: / Linia 216: @@
 Teraz <math>L_1</math> w równaniu drugim zastępujemy prawą stroną równania pierwszego: <center><math>L_2 = L_1(a+b)+L_2b = (L_2a^2+a)(a+b)+L_2b =
-L_2(a^3+a^2b+b)+a^2+ab.</math></center>
+L_2(a^3+a^2b+b)+a^2+ab</math>.</center>
 Korzystamy z lematu Ardena i otrzymujemy
 <math>L_2=(a^2+ab)(a^3+a^2b+b)^*</math>. Podstawiamy to do równania
 <math>L_0=L_2a+1</math> i otrzymujemy ostatecznie:
-<center><math>L_0=(a^2+ab)(a^3+a^2b+b)^*a+1= (a^2+ab)(a^2(a+b)+b)^*a+1.</math></center>
+<center><math>L_0=(a^2+ab)(a^3+a^2b+b)^*a+1= (a^2+ab)(a^2(a+b)+b)^*a+1</math>.</center>
 Można pokazać, że wyrażenie to jest równoważne następującemu:
-<center><math>L_0=(a(a+b)b^*a)^*.</math></center>
+<center><math>L_0=(a(a+b)b^*a)^*</math>.</center>
 </div></div>
 {{cwiczenie|4||
@@ Linia 259: / Linia 259: @@
 <center><math>w \in L(\mathcal{A}) \cap L(\mathcal{B}) \Longleftrightarrow
-ww \in L(\mathcal{C}) \wedge f(s_0,w) \cap T_A \not = \emptyset.</math></center>
+ww \in L(\mathcal{C}) \wedge f(s_0,w) \cap T_A \not = \emptyset</math>.</center>
 Oba warunki występujące po prawej stronie równoważności są
@@ Linia 398: / Linia 398: @@
 (Twierdzenie 1.1, punkt 5.).
-.  <math>\exists s \in S, w_1, w_2 \in A^*:\ f(s_0, w_1)=s \wedge f(s,w_2)=s...</math>
+.  <math>\exists s \in S, w_1, w_2 \in A^*:\ f(s_0, w_1)=s \wedge f(s,w_2)=s..</math>.
 </div></div>

Języki, automaty i obliczenia/Ćwiczenia 8: Dalsze algorytmy dla języków regularnych. Problemy rozstrzygalne: Różnice pomiędzy wersjami

Wersja z 09:21, 5 wrz 2023

Menu nawigacyjne

Działania na stronie

Opcje strony

Narzędzia osobiste

Nawigacja

Szukaj

Narzędzia