PEE Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 363: | Linia 363: | ||
<math>U_2\approx - | <math>U_2\approx -\frac{X_M}{X_{L1}}U_1</math> | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd22.png]] | |||
|valign="top"|Jeśli uwzględnimy, że reaktancje cewek są proporcjonalne do liczby zwojów według relacji <math>X_{L1}=Kz_1^2, X_{L2}=Kz_2^2, X_M=Kz_1z_2</math> gdzie K oznacza pewną stałą konstrukcyjną, to z zależności wynika | |||
<math>\frac{U_2}{U_1}=-\frac{z_2}{z_1}=-\frac{1}{n}</math> | |||
Napięcie wtórne transformatora jest zależne wyłącznie od przekładni zwojowej i napięcia wejściowego układu (znak minus nie odgrywa żadnej roli a jedynie oznacza przesunięcie fazowe <math>180^o\,</math> napięcia wyjściowego względem wejściowego). Jest to zatem realizacja podstawowej zależności charakterystycznej dla transformatora idealnego. Przy pominięciu strat w transformatorze moc na wejściu równa się mocy wyjściowej, stąd relacja między prądem pierwotnym i wtórnym spełnia również drugą zależność transformatora idealnego ). Wynika stąd wniosek, że transformator z rdzeniem ferromagnetycznym jest dobrym przybliżeniem transformatora idealnego. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
Wersja z 10:53, 1 sie 2006

|
Wykład 5. Obwody ze sprzężeniami magnetycznymi |
|
|
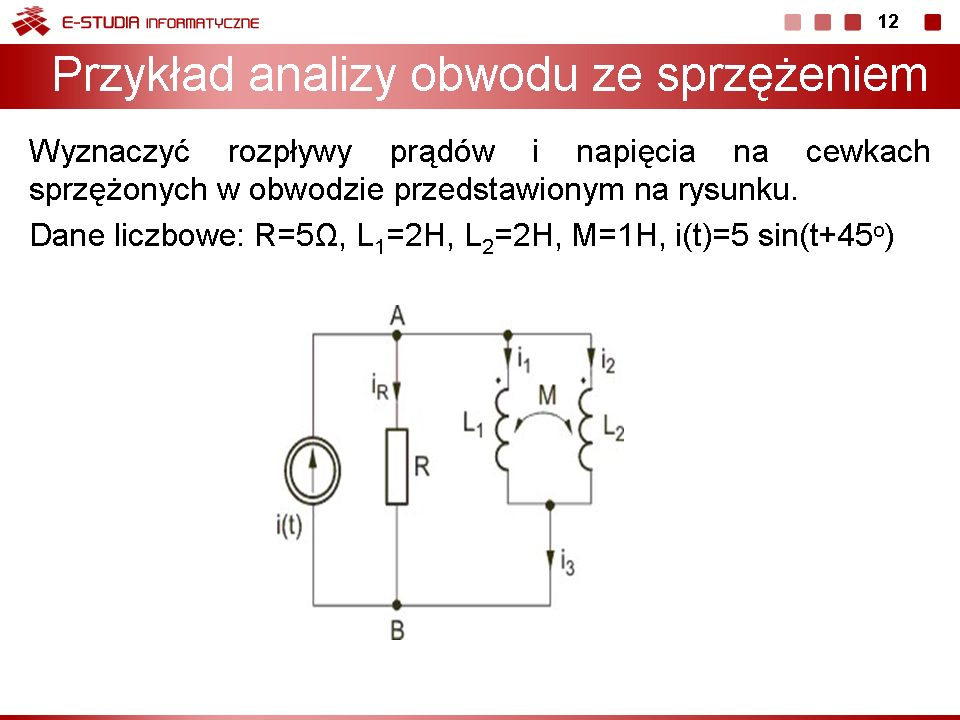
PRZYKŁAD
Wyznaczyć rozpływy prądów w obwodzie przedstawionym na rysunku Przyjąć następujące wartości parametrów elementów obwodu: oraz . |

|
Rozwiązanie
Postać obwodu po eliminacji sprzężenia magnetycznego przedstawiono na rysunku |

|
Wielkości symboliczne charakteryzujące elementy obwodu:
Impedancja zastępcza obwodu wobec
|