PEE Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 358: | Linia 358: | ||
<math>U_2=-[\frac{X_M}{X_{L1}}U_1+jI_2(\frac{X_{L1}X_{L2}-X_M^2}{X_{L1}})]</math> | <math>U_2=-[\frac{X_M}{X_{L1}}U_1+jI_2(\frac{X_{L1}X_{L2}-X_M^2}{X_{L1}})]</math> | ||
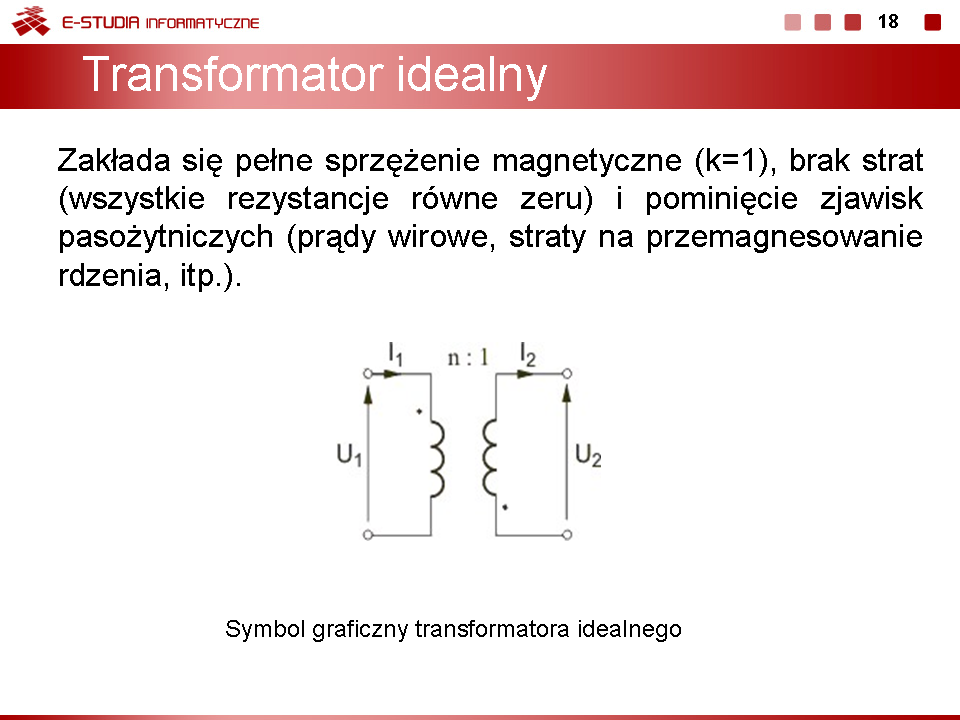
Przy założeniu wyidealizowanego transformatora <math>(k\approx 1 )</math> zachodzi <math>X_M^2\approx X_{L1}X_{L2}</math> . Oznacza to, że niezależnie od obciążenia relacja między napięciem pierwotnym i wtórnym dana jest w postaci | |||
<math>U_2\approx -|frac{X_M}{X_{L1}}U_1</math> | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
Wersja z 10:47, 1 sie 2006

|
Wykład 5. Obwody ze sprzężeniami magnetycznymi |
|
|
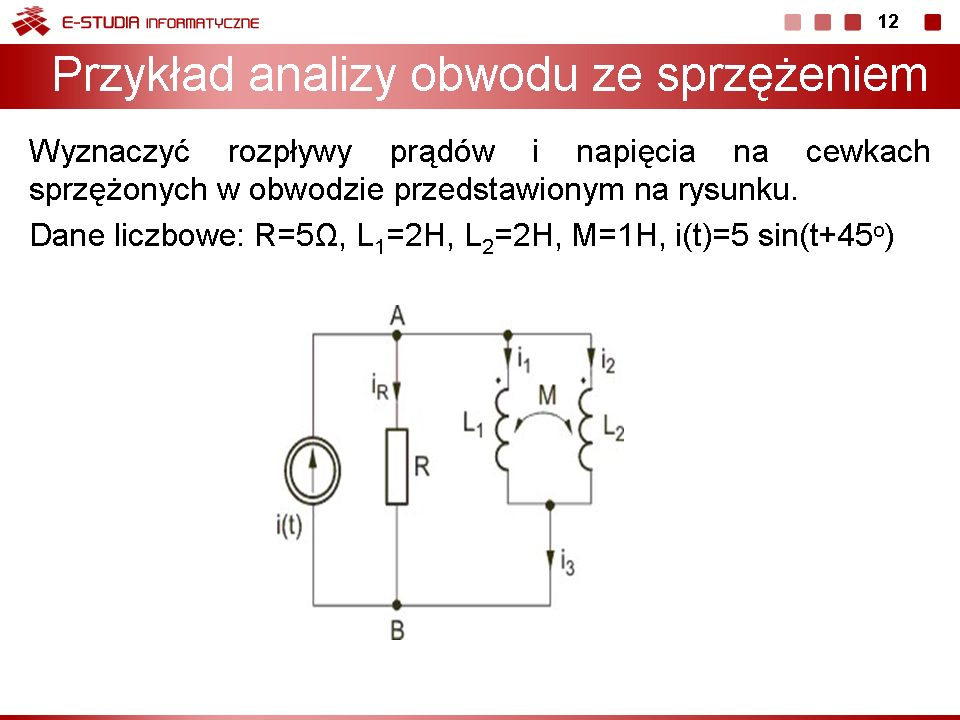
PRZYKŁAD
Wyznaczyć rozpływy prądów w obwodzie przedstawionym na rysunku Przyjąć następujące wartości parametrów elementów obwodu: oraz . |

|
Rozwiązanie
Postać obwodu po eliminacji sprzężenia magnetycznego przedstawiono na rysunku |

|
Wielkości symboliczne charakteryzujące elementy obwodu:
Impedancja zastępcza obwodu wobec
|