PEE Moduł 6: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 219: | Linia 219: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd15.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd15.png]] | ||
|valign="top"|* Odbiornik niesymetryczny przy zwartym przewodzie zerowym | |valign="top"| | ||
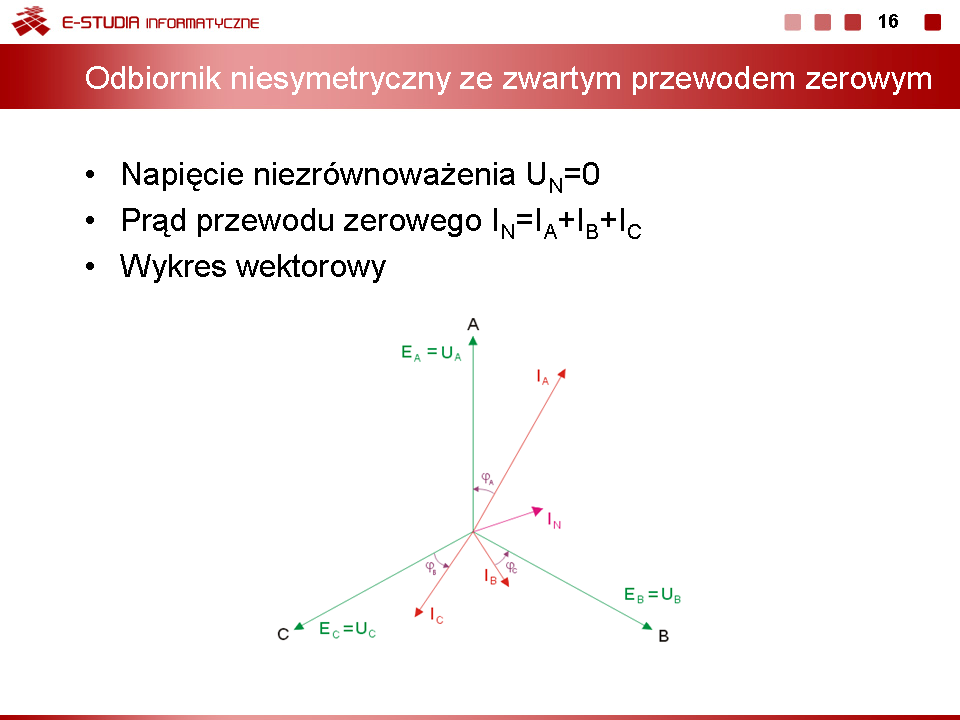
*Odbiornik niesymetryczny przy zwartym przewodzie zerowym | |||
W tym przypadku napięcie niezrównoważenia <math>U_N=0</math>, a prąd przewodu zerowego <math>I_N \neq 0</math>. Prądy fazowe są wówczas określane bezpośrednio na podstawie układu napięć generatorowych. Suma tych prądów w ogólnym przypadku odbiornika niesymetrycznego jest różna od zera | W tym przypadku napięcie niezrównoważenia <math>U_N=0</math>, a prąd przewodu zerowego <math>I_N \neq 0</math>. Prądy fazowe są wówczas określane bezpośrednio na podstawie układu napięć generatorowych. Suma tych prądów w ogólnym przypadku odbiornika niesymetrycznego jest różna od zera | ||
: <math>I_N=I_A+I_B+I_C</math> | |||
Wykres wektorowy prądów i napięć w układzie trójfazowym niesymetrycznym przy zwarciu bezimpedancyjnym punktów wspólnych odbiornika i generatora przedstawiony jest na rysunku poniżej (oraz na slajdzie nr 15). | |||
[[Grafika:PEE_M6_anim_5.gif]] | |||
|} | |} | ||
| Linia 230: | Linia 237: | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd16.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd16.png]] | ||
|valign="top"| | |valign="top"| | ||
*Zwarcie fazy odbiornika przy przerwie w przewodzie zerowym. | |||
W tym przypadku napięcie niezrównoważenia jest równe napięciu fazowemu fazy zwartej. | |||
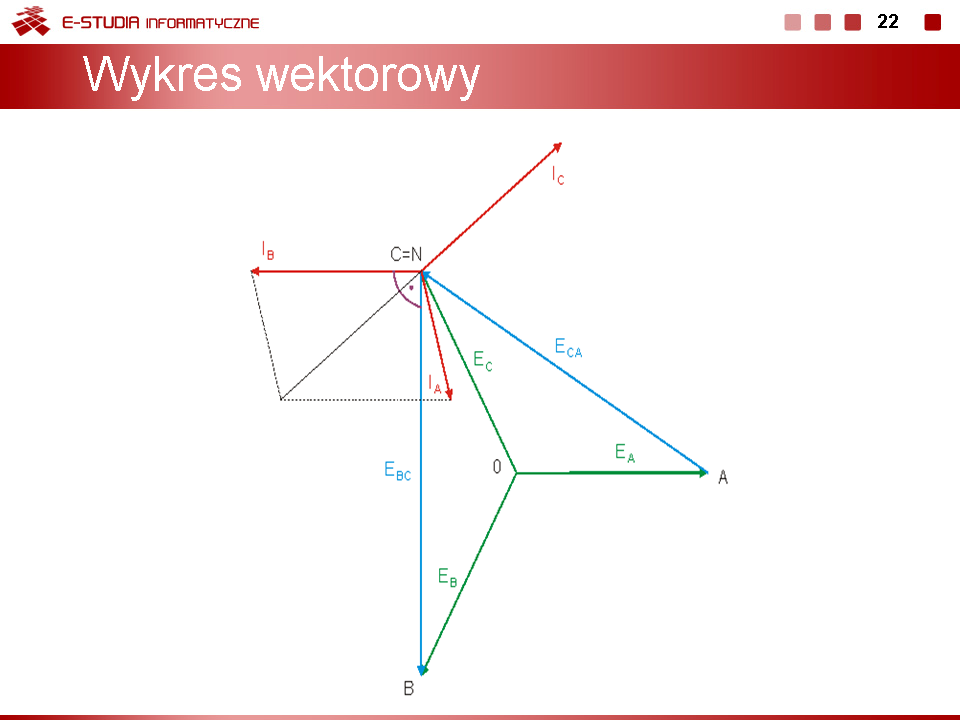
Prąd fazy zwartej nie może być określony z prawa Ohma, gdyż zarówno napięcie na fazie odbiornika jak i jego impedancja są równe zeru. Okresla sie go z prawa prądowego Kirchhoffa, zgodnie z którym | |||
: <math>I_A=-I_B-I_C</math> | |||
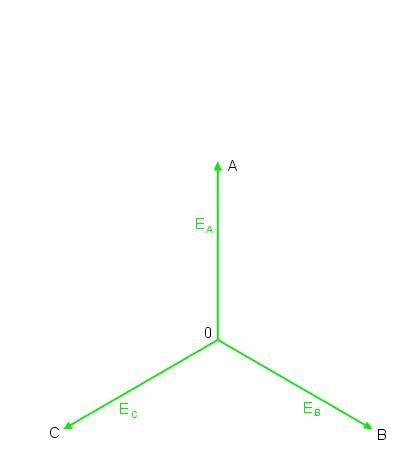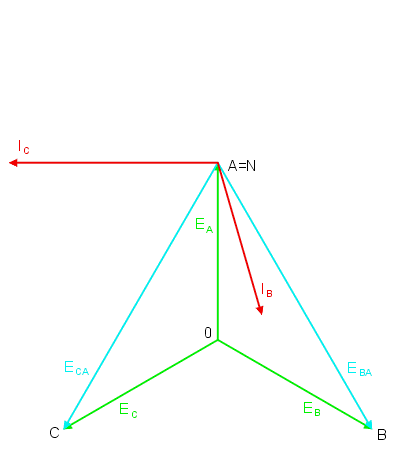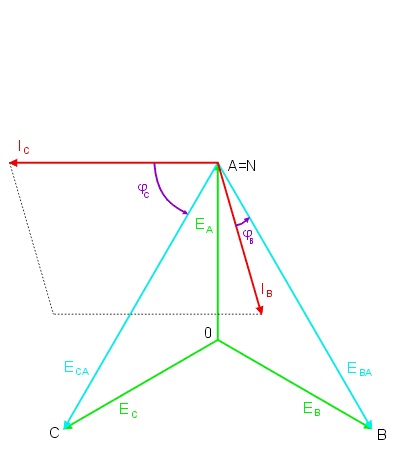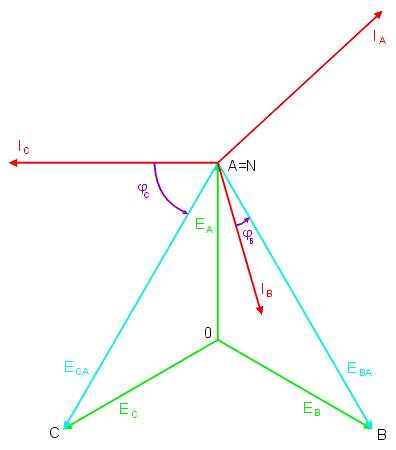
Wykres wektorowy prądów i napięć w układzie trójfazowym dla przypadku zwarcia fazy A odbiornika przedstawiony jest na rysunku poniżej (oraz na slajdzie nr 16). | |||
[[Grafika:PEE_M6_anim_6.gif]] | |||
|} | |} | ||
Wersja z 10:43, 1 sie 2006

|
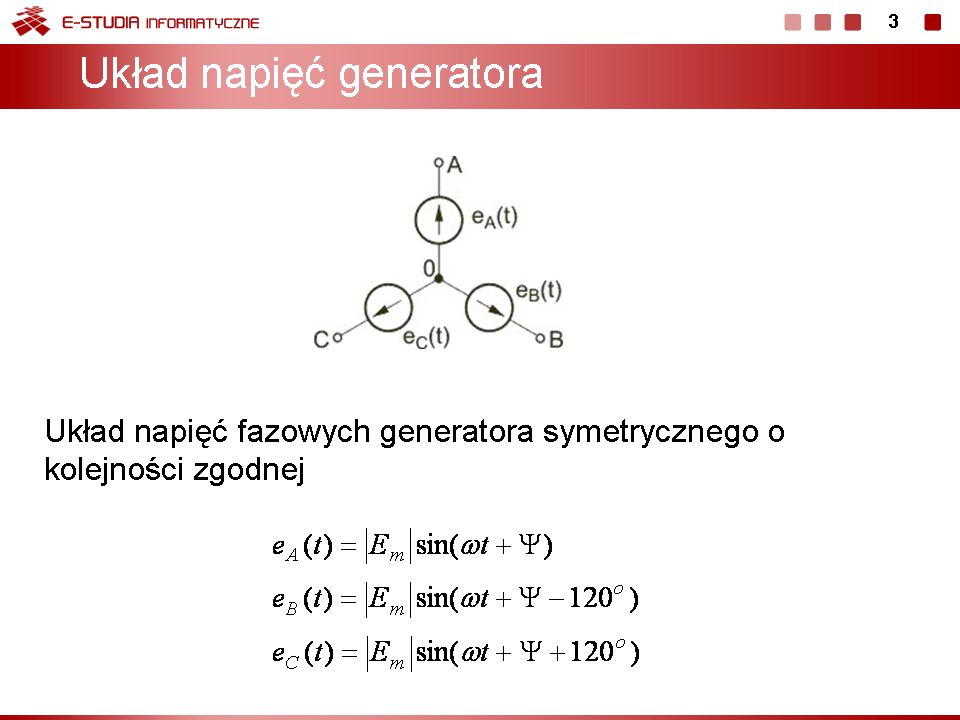
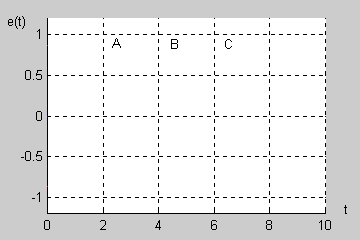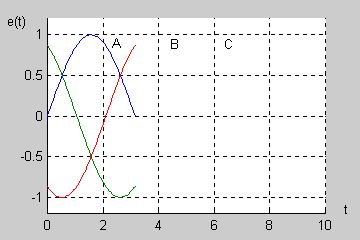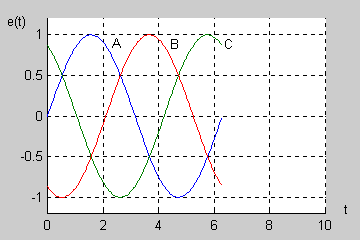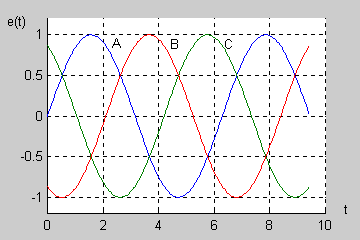
Wykład 6. Układy trójfazowe |

|
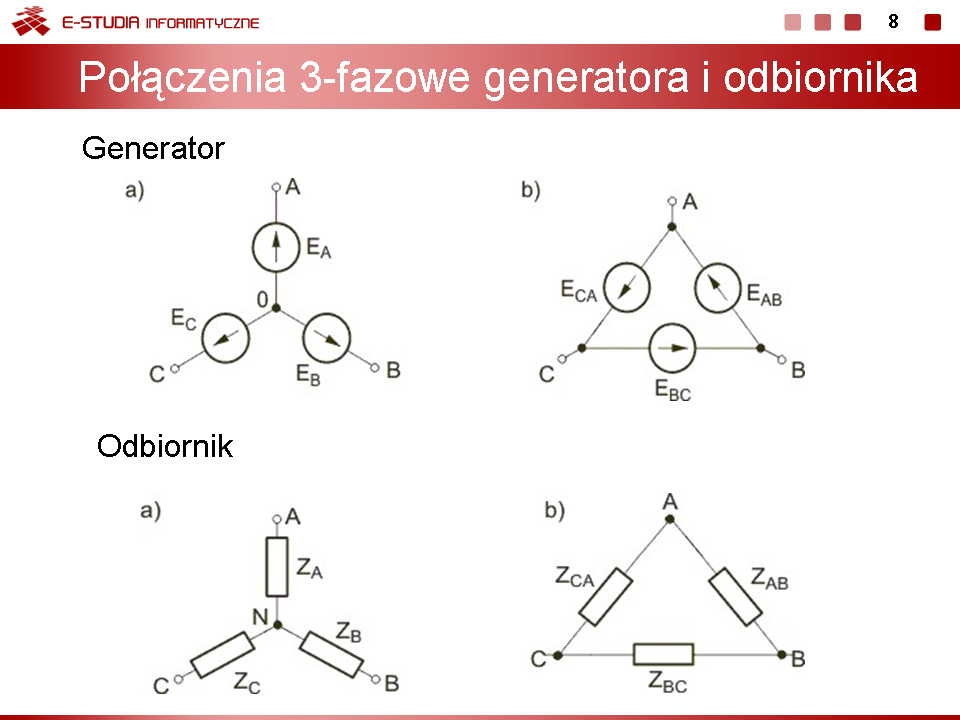
W pracy układu trójfazowego gwiazdowego można wyróżnić kilka szczególnych przypadków.
|

|

|

|

|
|

|

|