Matematyka dyskretna 1/Ćwiczenia 13: Grafy II: Różnice pomiędzy wersjami
m Zastępowanie tekstu - "<div class="thumb t(.*)"><div style="width:(.*)px;"> <flash>file=(.*)\.swf\|width=(.*)\|height=(.*)<\/flash> <div\.thumbcaption>(.*)<\/div><\/div> <\/div>" na "$4x$5px|thumb|$1|$6" |
m Zastępowanie tekstu – „\displaystyle ” na „” |
||
| Linia 2: | Linia 2: | ||
{{cwiczenie|1|cw 1| | {{cwiczenie|1|cw 1| | ||
Kostka <math> | Kostka <math>k </math> -wymiarowa <math>\mathcal{Q}_{k} </math> jest grafem, | ||
którego wierzchołki to ciągi <math> | którego wierzchołki to ciągi <math>\left( a_1,a_2,\ldots,a_k \right) </math> , gdzie <math>a_i=0,1 </math> , | ||
a krawędzie łączą te ciągi, które różnią się tylko na jednej pozycji. | a krawędzie łączą te ciągi, które różnią się tylko na jednej pozycji. | ||
Oblicz liczbę wierzchołków, krawędzi oraz rozmiar najdłuższego cyklu. | Oblicz liczbę wierzchołków, krawędzi oraz rozmiar najdłuższego cyklu. | ||
| Linia 10: | Linia 10: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Aby znaleźć liczbę wierzchołków policz liczbę <math> | Aby znaleźć liczbę wierzchołków policz liczbę <math>k </math> -elementowych ciągów złożonych | ||
z <math> | z <math>0 </math> i <math>1 </math> . | ||
Przy znalezieniu liczby krawędzi przydatna będzie znajomość stopnia wierzchołków. | Przy znalezieniu liczby krawędzi przydatna będzie znajomość stopnia wierzchołków. | ||
Najdłuższy cykl, to cykl przechodzący przez wszystkie wierzchołki. | Najdłuższy cykl, to cykl przechodzący przez wszystkie wierzchołki. | ||
Konstrukcję takiego cyklu przeprowadź indukcyjnie ze względu na <math> | Konstrukcję takiego cyklu przeprowadź indukcyjnie ze względu na <math>k </math> . | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
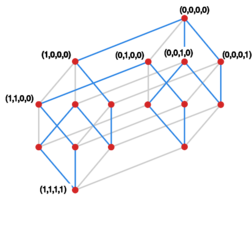
[[File:Cw grafy 4kostka.svg|350x250px|thumb|right" id="cw_grafy_4kostka|Cykl <math> | [[File:Cw grafy 4kostka.svg|350x250px|thumb|right" id="cw_grafy_4kostka|Cykl <math>16 </math> -elementowy w kostce <math>\mathcal{Q}_{4} </math>]] | ||
* Wierzchołki <math> | * Wierzchołki <math>\mathsf{ V}\!\left(\mathcal{Q}_{k}\right) </math> odpowiadają ciągom <math>\left( a_1,a_2,\ldots,a_k \right) </math> , gdzie <math>a_i=0,1 </math>. Liczba <math>k </math> -elementowych ciągów liczb z dwuelementowego zbioru wynosi <math>2^k </math> . | ||
* Z kolei krawędzie łączą te ciągi, które różnią się na jednej tylko pozycji. Ciąg ze względu na konkretną pozycję jest sąsiedni z dokładnie jednym ciągiem. Stopień dowolnego wierzchołka równy jest więc <math> | * Z kolei krawędzie łączą te ciągi, które różnią się na jednej tylko pozycji. Ciąg ze względu na konkretną pozycję jest sąsiedni z dokładnie jednym ciągiem. Stopień dowolnego wierzchołka równy jest więc <math>k </math>. Ponieważ każda krawędź ma dwa końce, to liczba wszystkich krawędzi jest równa <math>\frac{k\cdot 2^k}{2}=k\cdot 2^{k-1} </math> . | ||
* Najdłuższy cykl w <math> | * Najdłuższy cykl w <math>\mathcal{Q}_{k} </math> jest cyklem przechodzącym przez wszystkie wierzchołki. Wykażemy jego istnienie indukcyjnie ze względu na <math>k </math> , pokazując ścieżkę z wierzchołka <math>\left( 0,0,\ldots,0 \right) </math> do <math>\left( 1,0,\ldots,0 \right) </math> , przechodzącą przez wszystkie wierzchołki. | ||
Kostkę <math> | Kostkę <math>\mathcal{Q}_{k+1} </math> można rozłożyć na dwie kostki w ten sposób, że w pierwszej znajdą się wszystkie wierzchołki odpowiadające ciągom zaczynającym się od <math>0 </math> , czyli <math>\left( 0,a_2,\ldots,a_{k+1} \right) </math> , | ||
a w drugiej wierzchołki odpowiadające ciągom zaczynającym się od <math> | a w drugiej wierzchołki odpowiadające ciągom zaczynającym się od <math>1 </math> , czyli <math>\left( 1,a_2,\ldots,a_{k+1} \right) </math> . Na mocy założenia indukcyjnego otrzymujemy ścieżkę z wierzchołka <math>\left( 0,0,0,\ldots,0 \right) </math> do <math>\left( 0,1,0,\ldots,0 \right) </math> , przechodzącą przez wszystkie wierzchołki pierwszej kostki. Analogicznie otrzymujemy także ścieżkę z wierzchołka <math>\left( 1,0,0,\ldots,0 \right) </math> do <math>\left( 1,1,0,\ldots,0 \right) </math> , przechodzącą przez wszystkie wierzchołki drugiej kostki. Po złożeniu obu ścieżek w ścieżkę postaci | ||
<center><math> | <center><math>\begin{align} \left( 0,0,0,\ldots,0 \right)\to\ldots\to\left( 0,1,0,\ldots,0 \right)\to\left( 1,1,0,\ldots,0 \right)\to\ldots&&\\ | ||
\ldots\to\left( 1,0,0,\ldots,0 \right)&& | \ldots\to\left( 1,0,0,\ldots,0 \right)&& | ||
\end{align}</math></center> | \end{align}</math></center> | ||
otrzymujemy szukaną ścieżkę. W konsekwencji otrzymujemy, że najdłuższa ścieżka <math> | otrzymujemy szukaną ścieżkę. W konsekwencji otrzymujemy, że najdłuższa ścieżka <math>\mathcal{Q}_{k} </math> | ||
składa się ze wszystkich <math> | składa się ze wszystkich <math>2^k </math> wierzchołków. | ||
</div></div> | </div></div> | ||
{{cwiczenie|2|cw 2| | {{cwiczenie|2|cw 2| | ||
Dla jakich wartości <math> | Dla jakich wartości <math>n </math> grafy <math>\mathcal{K}_{n} </math> , <math>\mathcal{K}_{n,m} </math> , <math>\mathcal{Q}_{n} </math> są eulerowskie. | ||
}} | }} | ||
| Linia 50: | Linia 50: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Korzystając z twierdzenia [[Matematyka dyskretna 1/Wykład 13: Grafy II#tw_13.1|13.1]] otrzymujemy warunek, że każdy graf eulerowski musi posiadać jedynie wierzchołki o stopniu parzystym. | Korzystając z twierdzenia [[Matematyka dyskretna 1/Wykład 13: Grafy II#tw_13.1|13.1]] otrzymujemy warunek, że każdy graf eulerowski musi posiadać jedynie wierzchołki o stopniu parzystym. | ||
* W klice <math> | * W klice <math>\mathcal{K}_{n} </math> , każdy wierzchołek ma stopień równy <math>n-1 </math> , więc eulerowskimi są jedynie kliki <math>\mathcal{K}_{2k+1} </math> o <math>2k+1 </math> wierzchołkach, gdzie <math>k=0,1,2,\ldots </math> . | ||
* W pełnym grafie dwudzielnym <math> | * W pełnym grafie dwudzielnym <math>\mathcal{K}_{n,m} </math> wierzchołki mają stopnie równe <math>n </math> lub <math>m </math> . Wsród pełnych grafów dwudzielnych eulerowskie są jedynie grafy <math>\mathcal{K}_{2k,2l} </math> dla <math>k,l=0,1,2,\ldots </math> . | ||
* W kostce <math> | * W kostce <math>\mathcal{Q}_{n} </math> każdy wierzchołek ma <math>n </math> sąsiadów, więc eulerowskie są kostki <math>\mathcal{Q}_{2k} </math> dla <math>k=0,1,2,\ldots </math> . | ||
</div></div> | </div></div> | ||
| Linia 84: | Linia 84: | ||
{{cwiczenie|4|cw 4| | {{cwiczenie|4|cw 4| | ||
Dla jakich wartości <math> | Dla jakich wartości <math>n </math> grafy <math>\mathcal{K}_{n} </math> , <math>\mathcal{K}_{n,m} </math> , <math>\mathcal{Q}_{n} </math> | ||
są hamiltonowskie. | są hamiltonowskie. | ||
| Linia 90: | Linia 90: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Wyciągnij wnioski o liczności <math> | Wyciągnij wnioski o liczności <math>V_1 </math> oraz <math>V_2 </math> z istnienia cyklu Hamiltona | ||
w grafie <math> | w grafie <math>\mathcal{K}_{n,m}=\left( V_1\cup V_2,E \right) </math> . | ||
W odpowiedzi na pytanie, które kostki posiadają cykl Hamiltona, | W odpowiedzi na pytanie, które kostki posiadają cykl Hamiltona, | ||
wróć do ćwiczenia [[#cw_3|1]]. | wróć do ćwiczenia [[#cw_3|1]]. | ||
| Linia 97: | Linia 97: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
* Każda klika <math> | * Każda klika <math>n\geq 3 </math> elementowa jest hamiltonowska, ponieważ w klice dowolne dwa elementy są połączone krawędzią, | ||
dowolny ciąg wszystkich elementów tworzy więc cykl. | dowolny ciąg wszystkich elementów tworzy więc cykl. | ||
* W pełnym grafie dwudzielnym <math> | * W pełnym grafie dwudzielnym <math>\mathbf{G}=\left( V_1\cup V_2,E \right) </math> dowolna ścieżka ma na przemian wierzchołki ze zbiorów <math>V_1 </math> oraz <math>V_2 </math>, tzn. ścieżka ma postać | ||
<center><math> | <center><math>v_1\to v_2\to v_3\to \ldots v_k\to v_1, | ||
</math></center> | </math></center> | ||
gdzie <math> | gdzie <math>v_1, v_3, v_5,\ldots\in V_1 </math> , zaś <math>v_2, v_4, v_6,\ldots\in V_2 </math> . | ||
Jeżeli skojarzymy wierzchołek <math> | Jeżeli skojarzymy wierzchołek <math>v_1 </math> z wierzchołkiem <math>v_2 </math> , | ||
wierzchołek <math> | wierzchołek <math>v_3 </math> z wierzchołkiem <math>v_4 </math> | ||
i w ogólności <math> | i w ogólności <math>v_{2j+1} </math> z <math>v_{2j+2} </math> , | ||
to wykorzystamy wszystkie wierzchołki grafu <math> | to wykorzystamy wszystkie wierzchołki grafu <math>\mathbf{G} </math> . | ||
Skonstruowane zostało skojarzenie wierzchołków z <math> | Skonstruowane zostało skojarzenie wierzchołków z <math>V_1 </math> z wierzchołkami z <math>V_2 </math> | ||
wykorzystujące wszystkie wierzchołki, więc <math> | wykorzystujące wszystkie wierzchołki, więc <math>\left\vert V_1 \right\vert=\left\vert V_2 \right\vert </math> . | ||
Pełny graf dwudzielny <math> | Pełny graf dwudzielny <math>\mathcal{K}_{n,m} </math> jest więc hamiltonowski | ||
wtedy i tylko wtedy, gdy <math> | wtedy i tylko wtedy, gdy <math>n=m </math> . | ||
* Ścieżka o maksymalnej długości znaleziona w ćwiczeniu [[#wc_1|1]] jest ścieżką Hamiltona. Otrzymujemy więc wniosek, że każda kostka jest grafem hamiltonowskim. | * Ścieżka o maksymalnej długości znaleziona w ćwiczeniu [[#wc_1|1]] jest ścieżką Hamiltona. Otrzymujemy więc wniosek, że każda kostka jest grafem hamiltonowskim. | ||
| Linia 136: | Linia 136: | ||
{{cwiczenie|6|cw 6| | {{cwiczenie|6|cw 6| | ||
Podaj przykład grafu ilustrujący, że warunek <math> | Podaj przykład grafu ilustrujący, że warunek <math>\deg{v}\geq n/2 </math> | ||
występujący w Twierdzeniu Diraca [[Matematyka dyskretna 1/Wykład 13: Grafy II#wn_13.5|13.5]] | występujący w Twierdzeniu Diraca [[Matematyka dyskretna 1/Wykład 13: Grafy II#wn_13.5|13.5]] | ||
nie może być zastąpiony warunkiem <math> | nie może być zastąpiony warunkiem <math>\deg{v}\geq n/2-1 </math> . | ||
}} | }} | ||
| Linia 145: | Linia 145: | ||
Przeanalizuj dowód twierdzenia Ore'a (patrz tw. [[Matematyka dyskretna 1/Wykład 13: Grafy II#tw_13.4|13.4]]). | Przeanalizuj dowód twierdzenia Ore'a (patrz tw. [[Matematyka dyskretna 1/Wykład 13: Grafy II#tw_13.4|13.4]]). | ||
W którym miejscu załamałby się ten dowód, | W którym miejscu załamałby się ten dowód, | ||
gdyby istniały wierzchołki <math> | gdyby istniały wierzchołki <math>v,w </math> takie, że <math>\deg{v}+\deg{w}= n-1 </math> . | ||
</div></div> | </div></div> | ||
| Linia 153: | Linia 153: | ||
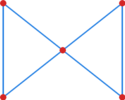
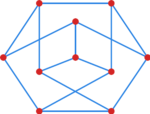
Jeżeli w wypowiedzi Twierdzenia Diraca, | Jeżeli w wypowiedzi Twierdzenia Diraca, | ||
warunek <math> | warunek <math>\deg{v}\geq n/2 </math> zastąpimy warunkiem <math>\deg{v}\geq n/2-1 </math> , | ||
to tak zmodyfikowane zdanie | to tak zmodyfikowane zdanie | ||
ma kontrprzykład przedstawiony na [[#cw grafy kontr dirac|rysunku]]. | ma kontrprzykład przedstawiony na [[#cw grafy kontr dirac|rysunku]]. | ||
| Linia 160: | Linia 160: | ||
{{cwiczenie|7|cw 7| | {{cwiczenie|7|cw 7| | ||
Wykaż, że <math> | Wykaż, że <math>n </math> elementowy <math>\mathbf{G} </math> jest hamiltonowski jeśli tylko | ||
ma przynajmniej <math> | ma przynajmniej <math>\left( n-1 \right)\left( n-2 \right)/2+2 </math> krawędzi. | ||
Podaj przykład grafu niehamiltonowskiego z <math> | Podaj przykład grafu niehamiltonowskiego z <math>n </math> wierzchołkami | ||
i <math> | i <math>\left( n-1 \right)\left( n-2 \right)/2+1 </math> krawędziami. | ||
}} | }} | ||
| Linia 173: | Linia 173: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
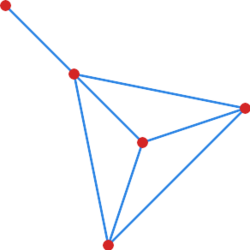
[[File:Cw grafy kontr moc v.svg|250x250px|thumb|right" id="cw_grafy_kontr_moc_v|Graf o <math> | [[File:Cw grafy kontr moc v.svg|250x250px|thumb|right" id="cw_grafy_kontr_moc_v|Graf o <math>5 </math> wierzchołkach i <math>7 </math> krawędziach, ale bez cyklu Hamiltona]] | ||
Niech <math> | Niech <math>u </math> i <math>v </math> będą niesąsiednimi wierzchołkami grafu <math>\mathbf{G} </math> . | ||
Dopełnienie grafu <math> | Dopełnienie grafu <math>\mathbf{G} </math> posiada co najwyżej | ||
<center> | <center> | ||
<math> | <math>\frac{n\left( n-1 \right)}{2}-\left( \frac{\left( n-1 \right)\left( n-2 \right)}{2}-2 \right)=n-3 | ||
</math> | </math> | ||
</center> | </center> | ||
krawędzi, więc <math> | krawędzi, więc <math>u </math> i <math>v </math> | ||
mogą być incydentne w sumie z co najwyżej <math> | mogą być incydentne w sumie z co najwyżej <math>n-3 </math> krawędziami w <math>\overline{\mathbf{G}} </math> . | ||
Liczba krawędzi incydentnych z <math> | Liczba krawędzi incydentnych z <math>u </math> lub <math>v </math> | ||
w grafie pełnym <math> | w grafie pełnym <math>\left( \mathsf{ V}\!\left(\mathbf{G}\right),\mathcal{P}_{2}\!\left( \mathsf{ V}\!\left(\mathbf{G}\right) \right) \right) </math> , | ||
jest równa <math> | jest równa <math>2n-3 </math> . | ||
Dopełnienie grafu <math> | Dopełnienie grafu <math>\mathbf{G} </math> jest to graf postaci | ||
<math> | <math>\overline{\mathbf{G}}=\left( \mathsf{ V}\!\left(\mathbf{G}\right),\mathcal{P}_{2}\!\left( \mathsf{ V}\!\left(\mathbf{G}\right) \right)-\mathsf{ E}\!\left(\mathbf{G}\right) \right) </math> , | ||
więc liczba krawędzi incydentnych z <math> | więc liczba krawędzi incydentnych z <math>u </math> lub <math>v </math> to co najmniej | ||
<center> | <center> | ||
<math> | <math>\left( 2n-3 \right)-\left( n-3 \right)=n. | ||
</math> | </math> | ||
</center> | </center> | ||
Wierzchołki <math> | Wierzchołki <math>u </math> i <math>v </math> nie sąsiadują ze sobą, | ||
więc zbiory incydentnych krawędzi są rozłączne, co w konsekwencji daje że | więc zbiory incydentnych krawędzi są rozłączne, co w konsekwencji daje że | ||
<center> | <center> | ||
<math> | <math>\mathsf{ deg}\ u+\mathsf{ deg}\ v\geq n. | ||
</math> | </math> | ||
</center> | </center> | ||
Na mocy więc Twierdzenia Ore'a (patrz tw. [[Matematyka dyskretna 1/Wykład 13: Grafy II#tw_13.4|13.4]]) otrzymujemy, że <math> | Na mocy więc Twierdzenia Ore'a (patrz tw. [[Matematyka dyskretna 1/Wykład 13: Grafy II#tw_13.4|13.4]]) otrzymujemy, że <math>\mathbf{G} </math> jest hamiltonowski. | ||
Wartość <math> | Wartość <math>\left( n-1 \right)\left( n-2 \right)/2+2 </math> jest najmniejszą taką liczbą, że każdy graf o <math>n </math> wierzchołkach i co najmniej tylu krawędziach jest hamiltonowski. Graf o <math>n=5 </math> wierzchołkach i <math>\left( n-1 \right)\left( n-2 \right)/2+1=7 </math> krawędziach, który nie jest hamiltonowski jest przedstawiony na rysunku [[#cw grafy kontr moc v|6]]. | ||
</div></div> | </div></div> | ||
| Linia 218: | Linia 218: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Dla drzewa <math> | Dla drzewa <math>T=\left( V,E \right) </math> wybierz dowolny wierzchołek <math>v\in V </math> | ||
i zdefiniuj odpowiedni podział <math> | i zdefiniuj odpowiedni podział <math>V=V_1\cup V_2 </math> korzystając z parzystości | ||
odległości od <math> | odległości od <math>v </math> . | ||
Kiedy pełny graf dwudzielny nie ma cykli? | Kiedy pełny graf dwudzielny nie ma cykli? | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Niech <math> | Niech <math>T=\left( V,E \right) </math> będzie drzewem a | ||
<math> | <math>v\in V </math> dowolnie wybranym jego wierzchołkiem. | ||
Podzielimy zbiór <math> | Podzielimy zbiór <math>V </math> na wierzchołki, które: | ||
* są oddalone od <math> | * są oddalone od <math>v </math> o odległość będącą liczbą parzystą - wraz z <math>v </math> będą tworzyć zbiór <math>V_1 </math> , | ||
* są oddalone od <math> | * są oddalone od <math>v </math> o odległość będącą liczbą nieparzystą - te z kolei będą składać się na zbiór <math>V_2 </math> . | ||
W drzewie pomiędzy dowolnymi wierzchołkami istnieje dokładnie jedna ścieżka, | W drzewie pomiędzy dowolnymi wierzchołkami istnieje dokładnie jedna ścieżka, | ||
tak więc ścieżka świadcząca o odległości wierzchołka <math> | tak więc ścieżka świadcząca o odległości wierzchołka <math>w </math> od wierzchołka <math>v </math> jest jedyną ścieżką pomiędzy <math>v </math> a <math>w </math> . Niech <math>ux\in E </math> dla wierzchołków <math>u,x\in V_i </math>. Ścieżka | ||
<center><math> | <center><math>v\to\ldots\to u\to x, | ||
</math></center> | </math></center> | ||
| Linia 242: | Linia 242: | ||
<center><math> | <center><math>v\to\ldots\to u, | ||
</math></center> | </math></center> | ||
co przeczy temu, że <math> | co przeczy temu, że <math>u </math> oraz <math>v </math> są razem w jednym zbiorze <math>V_i </math> . | ||
''Drzewo jest pełnym grafem dwudzielnym wtedy i tylko wtedy gdy jest gwiazdą.'' | ''Drzewo jest pełnym grafem dwudzielnym wtedy i tylko wtedy gdy jest gwiazdą.'' | ||
Istotnie, gwiazda o <math> | Istotnie, gwiazda o <math>n </math> liściach jest pełnym grafem dwudzielnym <math>\mathcal{K}_{1,n} </math> . | ||
Z drugiej strony załóżmy, że drzewo <math> | Z drugiej strony załóżmy, że drzewo <math>\mathbf{T}=\left( V_1\cup V_2, E \right) </math> | ||
jest pełnym grafem dwudzielnym, ale nie jest gwiazdą, | jest pełnym grafem dwudzielnym, ale nie jest gwiazdą, | ||
czyli zawiera ścieżkę o długości <math> | czyli zawiera ścieżkę o długości <math>3 </math> , np.: | ||
<center><math> | <center><math>u\to v\to w\to x. | ||
</math></center> | </math></center> | ||
Bez straty ogólności załóżmy, że <math> | Bez straty ogólności załóżmy, że <math>u\in V_1 </math> , | ||
tak więc <math> | tak więc <math>v,x\in V_2 </math> oraz <math>w\in V_1 </math> . | ||
W pełnym grafie dwudzielnym istnieje więc krawędź łącząca wierzchołek <math> | W pełnym grafie dwudzielnym istnieje więc krawędź łącząca wierzchołek <math>x\in V_2 </math> | ||
z wierzchołkiem <math> | z wierzchołkiem <math>u\in V_1 </math> . Mam więc cykl postaci: | ||
<center><math> | <center><math>u\to v\to w\to x\to u, | ||
</math></center> | </math></center> | ||
co przeczy temu, że <math> | co przeczy temu, że <math>\mathbf{T} </math> jest drzewem. | ||
</div></div> | </div></div> | ||
| Linia 282: | Linia 282: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Niech <math> | Niech <math>w </math> , <math>u </math> będą dwoma różnymi i niesąsiednimi wierzchołkami spójnego grafu | ||
<math> | <math>\mathbf{G} = \left( V,E \right) </math> . | ||
Przez <math> | Przez <math>k </math> oznaczmy najmniejszą możliwą | ||
liczność zbioru wierzchołków rozdzielających <math> | liczność zbioru wierzchołków rozdzielających <math>w </math> , <math>u </math> . | ||
Oczywiście każda droga łącząca <math> | Oczywiście każda droga łącząca <math>w </math> z <math>u </math> | ||
musi przejść przez każdy zbiór rozdzielający. | musi przejść przez każdy zbiór rozdzielający. | ||
A zatem dróg wierzchołkowo rozłącznych łączących <math> | A zatem dróg wierzchołkowo rozłącznych łączących <math>w </math> z <math>u </math> | ||
nie może być więcej niż <math> | nie może być więcej niż <math>k </math> . | ||
Tak więc wystarczy pokazać, | Tak więc wystarczy pokazać, | ||
że istnieje <math> | że istnieje <math>k </math> rozłącznych wierzchołkowo dróg z <math>w </math> do <math>u </math> . | ||
Dowód przeprowadzimy indukcyjnie ze względu na liczbę wierzchołków w grafie <math> | Dowód przeprowadzimy indukcyjnie ze względu na liczbę wierzchołków w grafie <math>\mathbf{G} </math> rozważając dwa przypadki. | ||
;1. Pewien zbiór rozdzielający <math> | ;1. Pewien zbiór rozdzielający <math>X </math> mocy <math>k </math> ma wierzchołek niesąsiedni z <math>w </math> oraz ma wierzchołek (być może inny) niesąsiedni z <math>u </math> . | ||
Graf <math> | Graf <math>\mathbf{G} </math> , po usunięciu wszystkich wierzchołków z <math>X </math> , podzieli się na dwie spójne składowe <math>W </math> oraz <math>U </math> , | ||
do których należą odpowiednio <math> | do których należą odpowiednio <math>w </math> i <math>u </math> . | ||
Przez <math> | Przez <math>W' </math> oznaczmy graf powstały z grafu <math>\mathbf{G} </math> poprzez ściągnięcie <math>U </math> w jeden wierzchołek <math>u' </math> . Wtedy <math>u' </math> jest połączony z tymi wierzchołkami <math>t\in X </math> , z którymi połączony był jakiś wierzchołek <math>s\in U </math> . Krawędzie łączące wierzchołki wewnątrz <math>W </math> pozostały niezmienione. Graf <math>U' </math> definiujemy analogicznie, poprzez ściągnięcie zbioru <math>W </math> do wierzchołka <math>w' </math> . | ||
W grafie <math> | W grafie <math>W' </math> minimalny zbiór rozdzielający wierzchołki <math>w, u' </math> posiada <math>k </math> wierzchołków. Ponieważ założyliśmy, ze w <math>X </math> istnieje wierzchołek niesąsiedni z <math>u </math> , to <math>U </math> ma co najmniej dwa wierzchołki, a zatem graf <math>W' </math> ma mniej wierzchołków niż <math>\mathbf{G} </math> . Tak wiec możemy skorzystać z założenia indukcyjnego otrzymując <math>k </math> rozłącznych wierzchołkowo dróg łączących <math>w </math> z <math>u' </math> w <math>W' </math> . Analogicznie w grafie <math>U </math> otrzymujemy <math>k </math> rozłącznych wierzchołkowo dróg łączących <math>w' </math> z <math>u </math> . Sklejając odpowiednio drogi z obu tych rodzin otrzymujemy <math>k </math> rozłącznych ścieżek łączących <math>w </math> z <math>u </math> w grafie <math>\mathbf{G} </math> . | ||
;2. W każdym zbiorze rozdzielającym <math> | ;2. W każdym zbiorze rozdzielającym <math>X </math> o mocy <math>k </math> , każdy wierzchołek jest sąsiedni do <math>w </math> lub do <math>u </math> . | ||
Możemy wtedy założyć, że <math> | Możemy wtedy założyć, że <math>\mathbf{G} </math> poza <math>w,u </math> zawiera jedynie wierzchołki należące do któregoś zbioru rozdzielającego <math>w, u </math> | ||
o liczności <math> | o liczności <math>k </math> . Gdyby tak nie było i istniałby jakiś inny wierzchołek <math>v </math> , to moglibyśmy <math>v </math> usunąć i, na mocy założenia indukcyjnego, | ||
otrzymać natychmiast <math> | otrzymać natychmiast <math>k </math> rozłącznych dróg łączących <math>w, u </math> . Tak wiec pozostały nam jedynie te wierzchołki, które są w minimalnych zbiorach rozdzielających <math>w, u </math> . To zaś, zgodnie z założeniem przypadku 2 oznacza, że każdy wierzchołek jest sąsiedni z <math>w </math> lub z <math>u </math> . W ten sposób drugi przypadek sprowadziliśmy do sytuacji, w której każda ścieżka z <math>w </math> do <math>u </math> ma co najwyżej dwie krawędzie. | ||
Wśród takich ścieżek nietrudno jest już wskazać <math> | Wśród takich ścieżek nietrudno jest już wskazać <math>k </math> rozłącznych wierzchołkowo. | ||
</div></div> | </div></div> | ||
| Linia 318: | Linia 318: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Dla grafu dwudzielnego <math> | Dla grafu dwudzielnego <math>\mathbf{G}=\left( V_1\cup V_2,E \right) </math> , | ||
oraz funkcji <math> | oraz funkcji <math>\Phi\!\left(A\right) </math> , | ||
która zwraca zbiór wierzchołków z <math> | która zwraca zbiór wierzchołków z <math>V_2 </math> | ||
sąsiednich z przynajmniej jednym wierzchołkiem w <math> | sąsiednich z przynajmniej jednym wierzchołkiem w <math>A\subseteq V_1 </math> | ||
twierdzenie Hall'a (patrz tw. [[Matematyka dyskretna 1/Wykład 13: Grafy II#tw_13.7|13.7]]) mówi, że: | twierdzenie Hall'a (patrz tw. [[Matematyka dyskretna 1/Wykład 13: Grafy II#tw_13.7|13.7]]) mówi, że: | ||
''Pełne skojarzenie <math> | ''Pełne skojarzenie <math>V_1 </math> z <math>V_2 </math> istnieje wtedy i tylko wtedy, gdy <math>\left\vert A \right\vert \leq\left\vert \Phi\!\left(A\right) \right\vert </math> , dla każdego podzbioru <math>A </math> zbioru <math>V_1 </math> .'' | ||
<math> | <math>\Rightarrow </math> Implikacja ta wynika natychmiast z faktu, że jeśli w pełnym skojarzeniu <math>V_1 </math> z <math>V_2 </math> , w <math>\Phi\!\left(A\right) </math> jest <math>\left\vert A \right\vert </math> wierzchołków skojarzonych z wierzchołkami z <math>A </math> , co w szczególności implikuje, że <math>\left\vert A \right\vert \leq\left\vert \Phi\!\left(A\right) \right\vert </math> . | ||
<math> | <math>\Leftarrow </math> Do grafu dwudzielnego <math>\mathbf{G}=\left( V_1\cup V_2,E \right) </math> | ||
dołóżmy dwa wierzchołki <math> | dołóżmy dwa wierzchołki <math>v_1 </math> oraz <math>v_2 </math> łącząc <math>v_1 </math> ze wszystkimi wierzchołkami z <math>V_1 </math> , a <math>v_2 </math> ze wszystkimi wierzchołkami z <math>V_2 </math> . Rozważmy dowolny zbiór <math>S\subseteq V_1\cup V_2 </math> o <math>\left\vert V_1 \right\vert-1 </math> wierzchołkach. Na mocy założenia otrzymujemy, że zbiór wierzchołków z <math>V_2 </math> sąsiadujących z wierzchołkami <math>V_1- S </math> jest co najmniej tak duży, jak <math>V_1- S </math> , czyli | ||
<center><math> | <center><math>\left\vert V_1- S \right\vert \leq\left\vert \Phi\!\left(V_1- S\right) \right\vert. | ||
</math></center> | </math></center> | ||
Ponieważ <math> | Ponieważ <math>\left\vert S \right\vert<\left\vert V_1 \right\vert </math> , to | ||
<math> | <math>\left\vert V_2\cap S \right\vert < \left\vert V_1- S \right\vert \leq\left\vert \Phi\!\left(V_1- S\right) \right\vert </math> , | ||
a zatem | a zatem | ||
<math> | <math>\Phi\!\left(V_1- S\right)- S\neq\emptyset </math> , | ||
czyli <math> | czyli <math>\Phi\!\left(V_1- S\right)\not\subseteq S </math> . | ||
Istnieją więc sąsiednie wierzchołki <math> | Istnieją więc sąsiednie wierzchołki <math>u_1\in V_1- S </math> | ||
oraz <math> | oraz <math>u_2\in\Phi\!\left(V_1- S\right)- S </math> . | ||
Teraz, ścieżka postaci | Teraz, ścieżka postaci | ||
<center><math> | <center><math>v_1\to u_1\to u_2\to v_2 | ||
</math></center> | </math></center> | ||
świadczy więc o tym, że <math> | świadczy więc o tym, że <math>S </math> nie był w stanie rozdzielić wierzchołka <math>v_1 </math> od <math>v_2 </math> . | ||
Na mocy wierzchołkowej wersji twierdzenia Mangera | Na mocy wierzchołkowej wersji twierdzenia Mangera | ||
(patrz ćw. [[#cw_9|9]]), | (patrz ćw. [[#cw_9|9]]), | ||
istnieje <math> | istnieje <math>\left\vert V_1 \right\vert </math> rozłącznych wierzchołkowo ścieżek łączących <math>v_1 </math> z <math>v_2 </math> . | ||
Każda taka ścieżka musi być postaci | Każda taka ścieżka musi być postaci | ||
<center><math> | <center><math>v_1\to w_1\to w_2\to v_2, | ||
</math></center> | </math></center> | ||
gdzie <math> | gdzie <math>w_1\in V_1 </math> oraz <math>w_2\in V_2 </math> . | ||
Istotnie ścieżek tych jest dokładnie <math> | Istotnie ścieżek tych jest dokładnie <math>\left\vert V_1 \right\vert </math> , | ||
więc każda z nich przechodzi dokładnie raz przez <math> | więc każda z nich przechodzi dokładnie raz przez <math>V_1 </math> i dokładnie raz | ||
przez <math> | przez <math>V_2 </math> . | ||
Usuwając teraz z każdej takiej ścieżki wierzchołki <math> | Usuwając teraz z każdej takiej ścieżki wierzchołki <math>v_1,v_2 </math> , | ||
otrzymujemy pełne skojarzenie <math> | otrzymujemy pełne skojarzenie <math>V_1 </math> z <math>V_2 </math> . | ||
</div></div> | </div></div> | ||
Wersja z 08:59, 28 sie 2023
Grafy II
Ćwiczenie 1
Kostka -wymiarowa jest grafem, którego wierzchołki to ciągi , gdzie , a krawędzie łączą te ciągi, które różnią się tylko na jednej pozycji. Oblicz liczbę wierzchołków, krawędzi oraz rozmiar najdłuższego cyklu.
Ćwiczenie 2
Dla jakich wartości grafy , , są eulerowskie.
Ćwiczenie 3
Przedstaw cztery pięciowierzchołkowe grafy -- kolejno graf który:
- nie jest hamiltonowski i nie jest eulerowski
- nie jest hamiltonowski, ale jest eulerowski
- jest hamiltonowski i nie jest eulerowski
- jest hamiltonowski i eulerowski.
Rozwiązanie jest przedstawione na rysunku.
Ćwiczenie 4
Dla jakich wartości grafy , , są hamiltonowskie.
Ćwiczenie 5
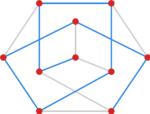
Czy graf Petersena (patrz rysunek) ma ścieżkę Hamiltona.
Ćwiczenie 6
Podaj przykład grafu ilustrujący, że warunek występujący w Twierdzeniu Diraca 13.5 nie może być zastąpiony warunkiem .
Ćwiczenie 7
Wykaż, że elementowy jest hamiltonowski jeśli tylko ma przynajmniej krawędzi. Podaj przykład grafu niehamiltonowskiego z wierzchołkami i krawędziami.
Ćwiczenie 8
Wykaż, że każde drzewo jest grafem dwudzielnym. Które drzewa są pełnymi grafami dwudzielnymi?
Ćwiczenie 9
Udowodnij wierzchołkową wersję Twierdzenia Mengera.
Ćwiczenie 10
Korzystając z Twierdzenia Mengera udowodnij Twierdzenie Halla o skojarzeniach w grafach dwudzielnych.