PEE Moduł 12: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „\displaystyle ” na „” |
||
| Linia 50: | Linia 50: | ||
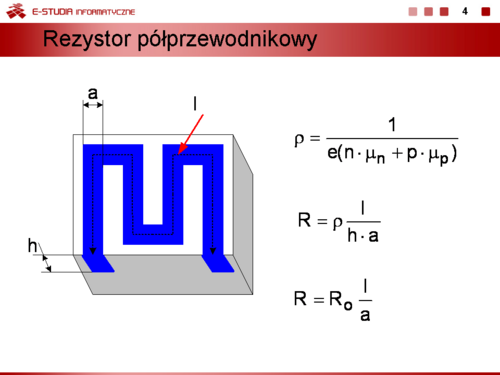
|valign="top"|'''Rezystor półprzewodnikowy. '''Jednym z podstawowych elementów każdego obwodu elektronicznego jest rezystor. W monolitycznych układach scalonych wytwarzanych na bazie kryształu krzemu także rezystory są wykonane z półprzewodnika. Ponieważ rezystywność półprzewodnika odpowiednio domieszkowanego jest opisana zależnością | |valign="top"|'''Rezystor półprzewodnikowy. '''Jednym z podstawowych elementów każdego obwodu elektronicznego jest rezystor. W monolitycznych układach scalonych wytwarzanych na bazie kryształu krzemu także rezystory są wykonane z półprzewodnika. Ponieważ rezystywność półprzewodnika odpowiednio domieszkowanego jest opisana zależnością | ||
:<math> | :<math>\rho=\frac{1}{e(n\cdot \mu_n+p\cdot \mu_p)}</math> | ||
to jej wartość może być w czasie trwania procesu technologicznego odpowiednio uformowana przez dobór koncentracji i rozkładu domieszek. W ten sposób w warstwie półprzewodnika samoistnego o dużej rezystywności można wytworzyć ścieżkę | to jej wartość może być w czasie trwania procesu technologicznego odpowiednio uformowana przez dobór koncentracji i rozkładu domieszek. W ten sposób w warstwie półprzewodnika samoistnego o dużej rezystywności można wytworzyć ścieżkę | ||
o wymaganej przewodności. Jeżeli ścieżka ma wymiary długość – l, szerokość – a oraz grubość – h to rezystancja warstwowego rezystora półprzewodnikowego jest równa: | o wymaganej przewodności. Jeżeli ścieżka ma wymiary długość – l, szerokość – a oraz grubość – h to rezystancja warstwowego rezystora półprzewodnikowego jest równa: | ||
:<math> | :<math>R=\rho \frac{l}{h\cdot a}</math> | ||
Grubość – h ścieżki rezystora wykonanego w konkretnym procesie technologicznym jest stała, zatem rezystancja rezystora zależy oprócz rezystywności ρ także od długości i szerokości wykonanej ścieżki. | Grubość – h ścieżki rezystora wykonanego w konkretnym procesie technologicznym jest stała, zatem rezystancja rezystora zależy oprócz rezystywności ρ także od długości i szerokości wykonanej ścieżki. | ||
:<math> | :<math>R_0=\rho \frac{l}{a}</math> | ||
gdzie <math> | gdzie <math>R_0= \frac{\rho}{h}</math> - rezystywność powierzchniowa warstwy. | ||
Wartość <math>R_0\,</math> jest stała dla danego procesu technologicznego i w zależności od domieszkowania waha się w zakresie 50 ÷ 250 <math>\Omega\,</math>. Istotne znaczenie praktyczne ma także kształt ścieżki. Często rezystory półprzewodnikowe wykonuje się w postaci meandra co pozwala ograniczyć powierzchnię, którą zajmują oraz zmniejszyć ich indukcyjność własną. | Wartość <math>R_0\,</math> jest stała dla danego procesu technologicznego i w zależności od domieszkowania waha się w zakresie 50 ÷ 250 <math>\Omega\,</math>. Istotne znaczenie praktyczne ma także kształt ścieżki. Często rezystory półprzewodnikowe wykonuje się w postaci meandra co pozwala ograniczyć powierzchnię, którą zajmują oraz zmniejszyć ich indukcyjność własną. | ||
| Linia 81: | Linia 81: | ||
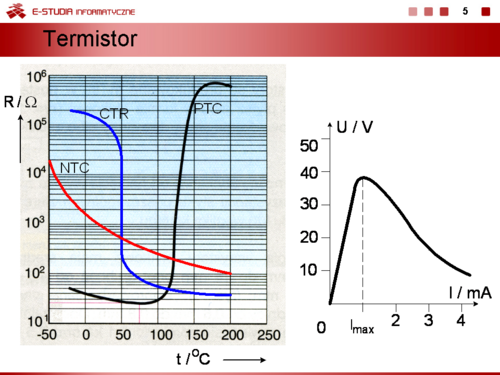
Rezystancja termistora NTC zmniejsz się ze wzrostem temperatury zgodnie z zależnością | Rezystancja termistora NTC zmniejsz się ze wzrostem temperatury zgodnie z zależnością | ||
:<math> | :<math>R_T=A\cdot e^{\frac{B}{T}}</math> | ||
gdzie A i B stałe materiałowe, T temperatura bezwzględna (K). | gdzie A i B stałe materiałowe, T temperatura bezwzględna (K). | ||
| Linia 89: | Linia 89: | ||
Ponieważ | Ponieważ | ||
:<math> | :<math>R_{T0}=A\cdot e^{\frac{B}{T_0}}</math> | ||
to po wyliczeniu A i wstawieniu do zależności | to po wyliczeniu A i wstawieniu do zależności | ||
<math> | <math>R_T=A\cdot e^{\frac{B}{T}}</math> otrzymujemy <math>R_T=R_{T_0}\cdot e^{(\frac{B}{T}-\frac{B}{T_0})}</math> | ||
Temperaturowy współczynnik rezystancji termistora definiowany następująco | Temperaturowy współczynnik rezystancji termistora definiowany następująco | ||
:<math> | :<math>d_T\left[\frac{\%}{C}\right]=\frac{1}{R_T}\frac{dR_T}{dT}</math> | ||
jest dla termistorów typu NTC ujemny i zawiera się w przedziale wartości od -3,5 do -6. | jest dla termistorów typu NTC ujemny i zawiera się w przedziale wartości od -3,5 do -6. | ||
| Linia 143: | Linia 143: | ||
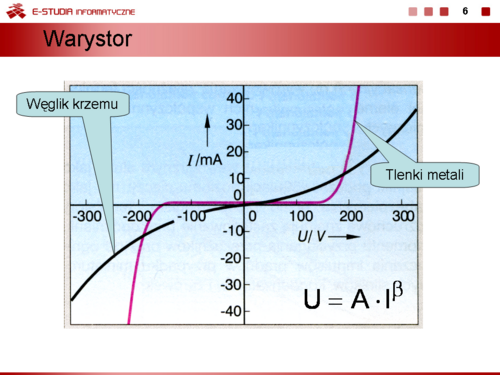
|valign="top"|'''Piezorezystor''' to element, którego rezystancja zależy od siły nacisku, jaki wywierany jest w osi poprzecznej elementu. Często zastępuje, w przypadku niewielkich odkształceń, klasyczny tensometr wykonany ze stopu oporowego. Czułość piezorezystora jest definiowana jako | |valign="top"|'''Piezorezystor''' to element, którego rezystancja zależy od siły nacisku, jaki wywierany jest w osi poprzecznej elementu. Często zastępuje, w przypadku niewielkich odkształceń, klasyczny tensometr wykonany ze stopu oporowego. Czułość piezorezystora jest definiowana jako | ||
:<math> | :<math>k=\frac{\displaystyle\frac{R}{R_0}}{\displaystyle\frac{I}{I_0}}</math> | ||
gdzie | gdzie | ||
| Linia 162: | Linia 162: | ||
|valign="top"|'''Magnetorezystor''' nazywany także gaussotronem to rezystor o rezystancji zależnej od pola magnetycznego, w którym go umieszczono. Zależność rezystancji od indukcji magnetycznej opisana jest wzorem | |valign="top"|'''Magnetorezystor''' nazywany także gaussotronem to rezystor o rezystancji zależnej od pola magnetycznego, w którym go umieszczono. Zależność rezystancji od indukcji magnetycznej opisana jest wzorem | ||
:<math> | :<math>R_B=R_0\cdot \frac{\rho_B}{\rho_0}\cdot f(\mu, B, a, b)</math> | ||
gdzie <math>R_0, \rho_0</math> – rezystancja i rezystywność elementu przy <math>B = 0\, T</math> | gdzie <math>R_0, \rho_0</math> – rezystancja i rezystywność elementu przy <math>B = 0\, T</math> | ||
| Linia 217: | Linia 217: | ||
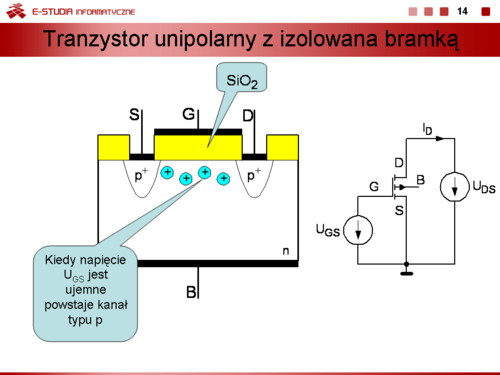
|valign="top"|Głębokość wnikania pola, a zatem i grubość warstwy inwersyjnej, a także ładunek elektryczny zgromadzony w warstwie inwersyjnej zależy od wartości napięcia <math>U_GB\,</math> | |valign="top"|Głębokość wnikania pola, a zatem i grubość warstwy inwersyjnej, a także ładunek elektryczny zgromadzony w warstwie inwersyjnej zależy od wartości napięcia <math>U_GB\,</math> | ||
:<math> | :<math>C_s=\frac{dQ_S}{dU_{GB}}</math> | ||
W tej sytuacji pojemność <math>C_s\,</math> jest połączona szeregowo ze stałą pojemnością warstwy dielektryka <math>C_i\,</math>, zależną od rozmiarów geometrycznych struktury i stałej elektrycznej dielektryka. Wypadkowa pojemność struktury jest równa | W tej sytuacji pojemność <math>C_s\,</math> jest połączona szeregowo ze stałą pojemnością warstwy dielektryka <math>C_i\,</math>, zależną od rozmiarów geometrycznych struktury i stałej elektrycznej dielektryka. Wypadkowa pojemność struktury jest równa | ||
:<math> | :<math>C=\frac{C_i\cdot C_s(U_{GB})}{C_i + C_s(U_{GB})}</math> | ||
|} | |} | ||
| Linia 255: | Linia 255: | ||
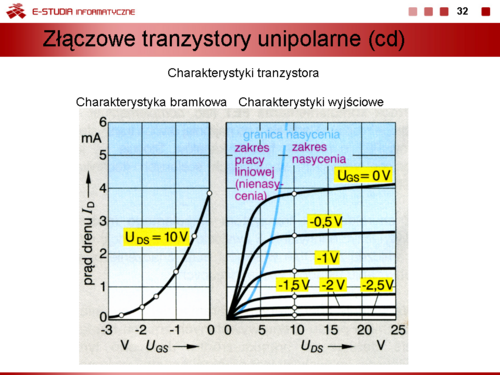
Rodzina charakterystyk wyjściowych ma taki sam przebieg dla tranzystorów z kanałem wzbogaconym jak i zubożonym. Dla małych wartości napięcia <math>U_{DS}\,</math> charakterystyka jest praktycznie liniowa, prąd drenu <math>I_D\,</math> rośnie w przybliżeniu proporcjonalnie do napięcia <math>U_{DS}\,</math>, a nachylenie charakterystyki tzn. wartość rezystancji kanału można zadawać napięciem <math>U_{GS}\,</math>. Dla napięć trochę większych, ale mniejszych od tzw. napięcia kolana <math>│U_{DS}│ < U_K = │U_{GS} - U_P│</math> rodzinę charakterystyk wyjściowych można opisać równaniem | Rodzina charakterystyk wyjściowych ma taki sam przebieg dla tranzystorów z kanałem wzbogaconym jak i zubożonym. Dla małych wartości napięcia <math>U_{DS}\,</math> charakterystyka jest praktycznie liniowa, prąd drenu <math>I_D\,</math> rośnie w przybliżeniu proporcjonalnie do napięcia <math>U_{DS}\,</math>, a nachylenie charakterystyki tzn. wartość rezystancji kanału można zadawać napięciem <math>U_{GS}\,</math>. Dla napięć trochę większych, ale mniejszych od tzw. napięcia kolana <math>│U_{DS}│ < U_K = │U_{GS} - U_P│</math> rodzinę charakterystyk wyjściowych można opisać równaniem | ||
:<math> | :<math>I_D=\frac{I_{DSS}}{U_P^2}[2\cdot |U_{GS}-U_P|\cdot |U_{DS}|-U_{DS}^2]</math> | ||
Ten zakres pracy nazywamy liniowym, nienasycenia lub triodowym. | Ten zakres pracy nazywamy liniowym, nienasycenia lub triodowym. | ||
| Linia 263: | Linia 263: | ||
<math>U_{DS}</math> i jest opisany równaniem | <math>U_{DS}</math> i jest opisany równaniem | ||
:<math> | :<math>I_D=I_{DSS}\left(1-\left|\frac{U_{GS}}{U_P}\right| \right)^2</math> | ||
a niewielką zależność ID od napięcia UDS charakteryzuje dynamiczna rezystancja wyjściowa | a niewielką zależność ID od napięcia UDS charakteryzuje dynamiczna rezystancja wyjściowa | ||
:<math> | :<math>r_{DS}=\frac{\delta U_{DS}}{\delta I_D}</math> dla <math>U_{GS}=const.</math> | ||
Prąd IDSS wyznaczyć można z charakterystyk bramkowych: dla tranzystorów z kanałem zubożonym przy <math>U_{GS} = 0\, V</math>, dla tranzystorów z kanałem wzbogaconym przy <math>U_{GS} = 2U_P</math>. | Prąd IDSS wyznaczyć można z charakterystyk bramkowych: dla tranzystorów z kanałem zubożonym przy <math>U_{GS} = 0\, V</math>, dla tranzystorów z kanałem wzbogaconym przy <math>U_{GS} = 2U_P</math>. | ||
| Linia 273: | Linia 273: | ||
Rodzina charakterystyk bramkowych (przejściowych) tranzystorów z kanałem typu n w zakresie napięć sterujących <math>U_{GS} > U_P</math> oraz z kanałem typu p w zakresie napięć <math>U_{GS} < U_P</math> opisana jest wzorem | Rodzina charakterystyk bramkowych (przejściowych) tranzystorów z kanałem typu n w zakresie napięć sterujących <math>U_{GS} > U_P</math> oraz z kanałem typu p w zakresie napięć <math>U_{GS} < U_P</math> opisana jest wzorem | ||
:<math> | :<math>I_D=I_{DSS}\left(1-\left|\frac{U_{GS}}{U_P}\right| \right)^2</math> | ||
Z charakterystyki bramkowej można wyznaczyć istotny z punktu widzenia wzmacniania sygnałów elektrycznych parametr tranzystora tzw. transkonduktancję gm lub inaczej nachylenie charakterystyki bramkowej S | Z charakterystyki bramkowej można wyznaczyć istotny z punktu widzenia wzmacniania sygnałów elektrycznych parametr tranzystora tzw. transkonduktancję gm lub inaczej nachylenie charakterystyki bramkowej S | ||
:<math> | :<math>g_m=S=\frac{\delta I_D}{\delta U_{GS}}</math> dla <math>U_{DS}=const.</math> | ||
Obserwując kształt charakterystyki bramkowej można stwierdzić, wśród tranzystorów z izolowaną bramką możemy wydzielić grupę tranzystorów normalnie załączonych, tzn. takich które przy <math>U_{DS} \neq 0\, V</math> i <math>U_{GS} = 0\, V</math>, przewodzą prąd drenu i grupę tranzystory normalnie wyłączonych, tzn. takich które w tych samych warunkach (<math>U_{DS} \neq 0\, V</math> i <math>U_{GS} = 0\, V</math>) nie przewodzą prądu drenu. | Obserwując kształt charakterystyki bramkowej można stwierdzić, wśród tranzystorów z izolowaną bramką możemy wydzielić grupę tranzystorów normalnie załączonych, tzn. takich które przy <math>U_{DS} \neq 0\, V</math> i <math>U_{GS} = 0\, V</math>, przewodzą prąd drenu i grupę tranzystory normalnie wyłączonych, tzn. takich które w tych samych warunkach (<math>U_{DS} \neq 0\, V</math> i <math>U_{GS} = 0\, V</math>) nie przewodzą prądu drenu. | ||
| Linia 324: | Linia 324: | ||
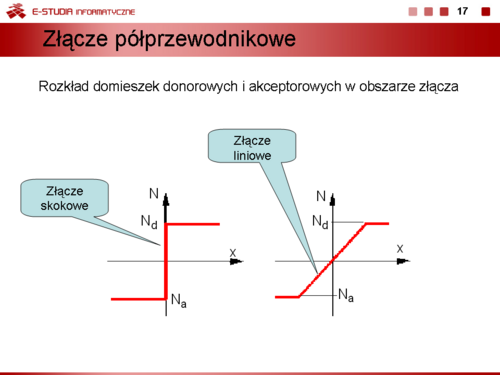
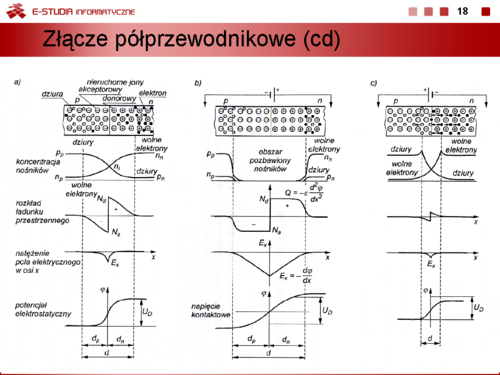
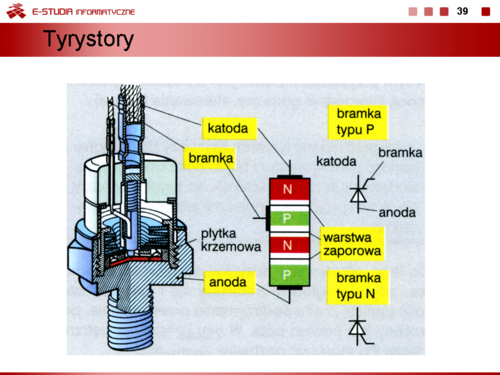
Nawet przy braku polaryzacji złącza na skutek ruchów cieplnych sieci krystalicznej półprzewodnika nośniki większościowe-elektrony z obszar typu n przenikają do obszaru o przewodnictwie dziurowym typu p i stają się tam nośnikami mniejszościowymi, a nośniki większościowe-dziury z obszaru p przenikają do obszaru typu n. W obszarze złącza następuje rekombinacja par elektron-dziura i w związku z tym w obszarze tym nie występuje swobodny ładunek. W pobliżu obszaru złącza w półprzewodniku typu n pozostają praktycznie nieruchome jony dodatnie, a w materiale typu p nieruchome jony ujemne. Te ładunki powodują, że na złączu wystąpi napięcie bariery potencjału lub krótko bariera potencjału | Nawet przy braku polaryzacji złącza na skutek ruchów cieplnych sieci krystalicznej półprzewodnika nośniki większościowe-elektrony z obszar typu n przenikają do obszaru o przewodnictwie dziurowym typu p i stają się tam nośnikami mniejszościowymi, a nośniki większościowe-dziury z obszaru p przenikają do obszaru typu n. W obszarze złącza następuje rekombinacja par elektron-dziura i w związku z tym w obszarze tym nie występuje swobodny ładunek. W pobliżu obszaru złącza w półprzewodniku typu n pozostają praktycznie nieruchome jony dodatnie, a w materiale typu p nieruchome jony ujemne. Te ładunki powodują, że na złączu wystąpi napięcie bariery potencjału lub krótko bariera potencjału | ||
:<math> | :<math>U_D=\frac{k\cdot T}{e}ln\frac{N_a\cdot N_d}{n_i}=\frac{e}{2\varepsilon}\left(N_d\cdot d_n^2+N_a\cdot d_p^2\right)</math> | ||
która zapobiega dalszemu przenikaniu ładunków przez obszar złącza. Warstwa ta staje się warstwą zaporową. Wychodząc z warunku równowagi ładunku w obszarze złącza | która zapobiega dalszemu przenikaniu ładunków przez obszar złącza. Warstwa ta staje się warstwą zaporową. Wychodząc z warunku równowagi ładunku w obszarze złącza | ||
| Linia 332: | Linia 332: | ||
można wyznaczenia szerokość tej warstwy zaporowej (szerokości złącza) | można wyznaczenia szerokość tej warstwy zaporowej (szerokości złącza) | ||
:<math> | :<math>d=d_p+d_n=\sqrt{\frac{2\varepsilon \cdot U_D\cdot (N_d+N_a)}{e\cdot N_d\cdot N_a}}</math> | ||
Warto zauważyć, że | Warto zauważyć, że | ||
:<math> | :<math>\frac{d_n}{d_p}=\frac{N_a}{N_d}</math> | ||
co oznacza, że ładunek jonowy wnika głębiej w obszar słabiej domieszkowany. | co oznacza, że ładunek jonowy wnika głębiej w obszar słabiej domieszkowany. | ||
| Linia 348: | Linia 348: | ||
i zależą od bariery potencjału <math>U_D</math> | i zależą od bariery potencjału <math>U_D</math> | ||
:<math> | :<math>Q_0=S\cdot e\cdot d_n\cdot N_d=S\cdot e\cdot d_p\cdot N_a=S\cqrt{2e\frac{N_d\cdot N_a}{N_d+N_a}U_D}</math> | ||
Pojemność takiego niespolaryzowanego napięciem zewnętrznym złącza jest równa | Pojemność takiego niespolaryzowanego napięciem zewnętrznym złącza jest równa | ||
:<math> | :<math>C_{T0}=\frac{Q_0}{2U_D}</math> | ||
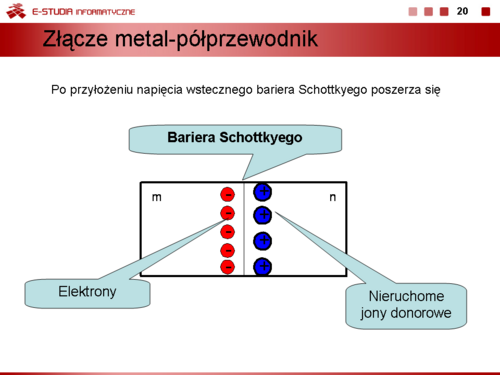
Po spolaryzowaniu złącza w kierunku zaporowym szerokość złącza zwiększa się | Po spolaryzowaniu złącza w kierunku zaporowym szerokość złącza zwiększa się | ||
:<math> | :<math>d=d_p+d_n=\sqrt{\frac{2\varepsilon \cdot( U_D+U)\cdot (N_d+N_a)}{e\cdot N_d\cdot N_a}}</math> | ||
Złącze takie można traktować jak kondensator. Pojemność warstwy zaporowej jest w tym wypadku równa | Złącze takie można traktować jak kondensator. Pojemność warstwy zaporowej jest w tym wypadku równa | ||
:<math> | :<math>C_T=\frac{dQ}{dU}=C_{T0}\sqrt{\frac{U_D}{U_D+U}}</math> | ||
Przy polaryzacji złącza w kierunku przewodzenia bariera potencjału znacznie obniża się ponieważ oba rodzaje nośników swobodnych dziury i elektrony poruszają się w kierunku złącza. Zmniejsza się szerokość i ładunek zgromadzony w warstwie zaporowej, maleje natężenie pola elektrycznego. W tym stanie rośnie gwałtownie dyfuzja nośników. Wzrasta liczba dziur przechodzących z obszaru półprzewodnika typu p do n i elektronów z obszaru n do p. Po przejściu przez złącze nośniki te stają się nośnikami mniejszościowymi | Przy polaryzacji złącza w kierunku przewodzenia bariera potencjału znacznie obniża się ponieważ oba rodzaje nośników swobodnych dziury i elektrony poruszają się w kierunku złącza. Zmniejsza się szerokość i ładunek zgromadzony w warstwie zaporowej, maleje natężenie pola elektrycznego. W tym stanie rośnie gwałtownie dyfuzja nośników. Wzrasta liczba dziur przechodzących z obszaru półprzewodnika typu p do n i elektronów z obszaru n do p. Po przejściu przez złącze nośniki te stają się nośnikami mniejszościowymi | ||
| Linia 367: | Linia 367: | ||
Ponieważ ładunek mniejszościowy wstrzykiwany do obszarów p i n w pobliżu złącza nie od razu rekombinuje zatem można mu przypisać pewną pojemność elektryczną zwana pojemnością dyfuzyjną. Ładunek dyfuzyjny wstrzykiwanych nośników mniejszościowych jest proporcjonalny do prądu I płynącego przez złącze, a ponieważ prąd I jest funkcja napięcia zasilania U to pojemność dyfuzyjną można obliczyć z zależności | Ponieważ ładunek mniejszościowy wstrzykiwany do obszarów p i n w pobliżu złącza nie od razu rekombinuje zatem można mu przypisać pewną pojemność elektryczną zwana pojemnością dyfuzyjną. Ładunek dyfuzyjny wstrzykiwanych nośników mniejszościowych jest proporcjonalny do prądu I płynącego przez złącze, a ponieważ prąd I jest funkcja napięcia zasilania U to pojemność dyfuzyjną można obliczyć z zależności | ||
:<math> | :<math>C_D=\frac{dQ}{dU}=\frac{\tau}{U_D}\cdot I</math> | ||
gdzie <math>\tau\,</math> – czas życia nośników mniejszościowych (zakłada się, że czasy życia dziur | gdzie <math>\tau\,</math> – czas życia nośników mniejszościowych (zakłada się, że czasy życia dziur | ||
| Linia 471: | Linia 471: | ||
Dla procesu załączania istotnymi parametrami są zatem: | Dla procesu załączania istotnymi parametrami są zatem: | ||
:<math> | :<math>\frac{di_F}{dt}</math> – maksymalna stromość narastania prądu przewodzenia oraz | ||
:<math>t_{fr}</math> - czas ustalania się napięcia przewodzenia. | :<math>t_{fr}</math> - czas ustalania się napięcia przewodzenia. | ||
| Linia 488: | Linia 488: | ||
<math>U_{Z0}</math> – napięcie przebicia (napięcie Zenera) | <math>U_{Z0}</math> – napięcie przebicia (napięcie Zenera) | ||
<math>r_Z\,</math> – rezystancję dynamiczną, gdzie <math> | <math>r_Z\,</math> – rezystancję dynamiczną, gdzie <math>r_Z=\frac{\Delta U_Z}{\Delta I_Z}</math> | ||
<math>P_{tot}\,</math> – moc strat | <math>P_{tot}\,</math> – moc strat | ||
| Linia 580: | Linia 580: | ||
Z charakterystyki wyjściowej można wyznaczyć rezystancją dynamiczną tranzystora | Z charakterystyki wyjściowej można wyznaczyć rezystancją dynamiczną tranzystora | ||
:<math> | :<math>r_{DS}=\frac{\delta U_{DS}}{\delta I_D}</math> dla <math>U_{GS} = const.</math> | ||
a z charakterystyki bramkowej istotny z punktu widzenia wzmacniania sygnałów elektrycznych parametr tzw. transkonduktancję <math>g_m\,</math> lub inaczej nachylenie charakterystyki bramkowej S | a z charakterystyki bramkowej istotny z punktu widzenia wzmacniania sygnałów elektrycznych parametr tzw. transkonduktancję <math>g_m\,</math> lub inaczej nachylenie charakterystyki bramkowej S | ||
:<math> | :<math>g_m=S=\frac{\delta I_D}{\delta U_{GS}}</math> przy <math>U_{DS} = const.</math> | ||
Charakterystyka bramkowa (przejściowa) tranzystora jest opisana wzorem | Charakterystyka bramkowa (przejściowa) tranzystora jest opisana wzorem | ||
| Linia 612: | Linia 612: | ||
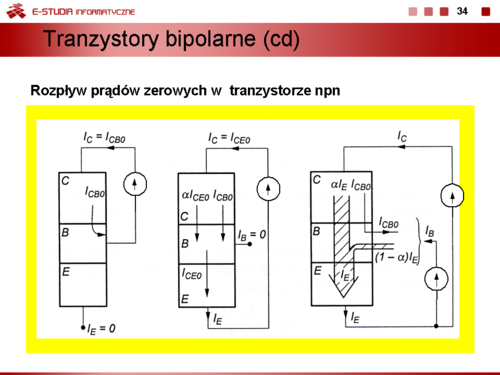
Zatem prądy zerowe w tranzystorze wiąże równanie | Zatem prądy zerowe w tranzystorze wiąże równanie | ||
:<math> | :<math>I_{CE0}=I_{CB0}\frac{1}{1-\alpha_0}</math> | ||
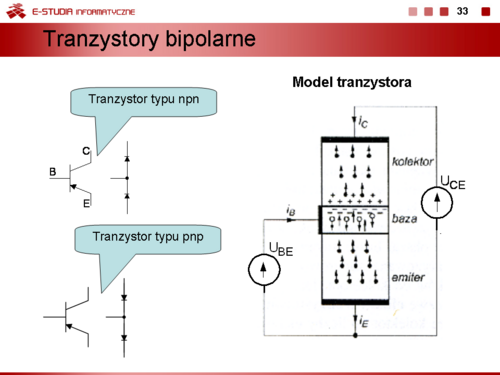
Prądy zerowe w tranzystorze są efektem zjawiska generacji termicznej nośników mniejszościowych. W wypadku złącza kolektor-baza jest to prąd wsteczny tego złącza. Można go zmierzyć przy odłączonym emiterze w układzie jak na rysunku. | Prądy zerowe w tranzystorze są efektem zjawiska generacji termicznej nośników mniejszościowych. W wypadku złącza kolektor-baza jest to prąd wsteczny tego złącza. Można go zmierzyć przy odłączonym emiterze w układzie jak na rysunku. | ||
| Linia 629: | Linia 629: | ||
Współczynnik <math>\alpha_0\,</math> nazywamy statycznym współczynnikiem wzmocnienia prądowego w układzie wspólnej bazy. | Współczynnik <math>\alpha_0\,</math> nazywamy statycznym współczynnikiem wzmocnienia prądowego w układzie wspólnej bazy. | ||
:<math> | :<math>\alpha_0=\frac{I_C-I_{CB0}}{I_E}\cong \frac{I_C}{I_E}</math> | ||
Dla układu wspólnego emitera statyczny współczynnik wzmocnienia prądowego jest definiowany jako | Dla układu wspólnego emitera statyczny współczynnik wzmocnienia prądowego jest definiowany jako | ||
:<math> | :<math>\beta_0=\frac{I_C-I_{CB0}}{I_B+I_{CB0}}=\frac{\alpha_0\cdot I_E}{I_B+I_C-\alpha_0\cdot I_E}=\frac{1}{1-\alpha_0}\cong \frac{I_C}{I_B}</math> | ||
a zatem | a zatem | ||
:<math> | :<math>\beta_0+1=\frac{1}{1-\alpha_0}</math> | ||
Uwzględniając prąd bazy równanie prądu kolektora przyjmie postać | Uwzględniając prąd bazy równanie prądu kolektora przyjmie postać | ||
| Linia 645: | Linia 645: | ||
Oprócz statycznych współczynników wzmocnienia prądowego (inaczej dla dużych sygnałów lub dla prądu stałego) stosuje się także dynamiczne (małosygnałowe, przyrostowe lub dla składowej zmiennej) współczynniki wzmocnienia prądowego | Oprócz statycznych współczynników wzmocnienia prądowego (inaczej dla dużych sygnałów lub dla prądu stałego) stosuje się także dynamiczne (małosygnałowe, przyrostowe lub dla składowej zmiennej) współczynniki wzmocnienia prądowego | ||
:<math> | :<math>\alpha=\frac{i_C}{i_E}\bigg|_{u_{CB}=0}=\frac{\Delta I_C}{\Delta I_E}\bigg|_{U_{CB}=const </math> | ||
:<math> | :<math>\beta=\frac{i_C}{i_B}\bigg|_{u_{CE}=0}=\frac{\Delta I_C}{\Delta I_B}\bigg|_{U_{CE}=const </math> | ||
| Linia 660: | Linia 660: | ||
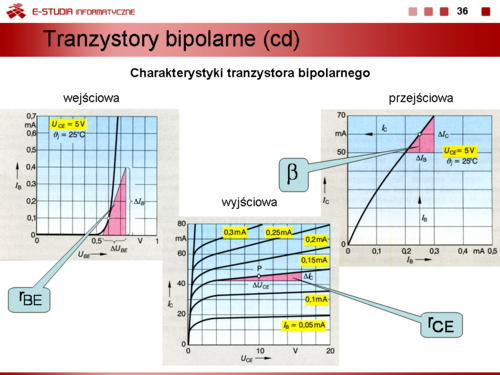
Dla obwodu wejściowego wyznacza się charakterystykę wejściową. Jest to zależność <math>I_B = f(U_{BE})</math> przy <math>U_{CE} = const.</math> Ponieważ wpływ napięcia <math>U_{CE}</math> na przebieg tej charakterystyki jest znikomy w szerokim zakresie zmienności tego napięcia rodzinę tych charakterystyk wyznacza linia przedstawiona na rysunku. Z charakterystyki tej można wyznaczyć dynamiczną rezystancję wejściową tranzystora <math>r_{BE}</math> | Dla obwodu wejściowego wyznacza się charakterystykę wejściową. Jest to zależność <math>I_B = f(U_{BE})</math> przy <math>U_{CE} = const.</math> Ponieważ wpływ napięcia <math>U_{CE}</math> na przebieg tej charakterystyki jest znikomy w szerokim zakresie zmienności tego napięcia rodzinę tych charakterystyk wyznacza linia przedstawiona na rysunku. Z charakterystyki tej można wyznaczyć dynamiczną rezystancję wejściową tranzystora <math>r_{BE}</math> | ||
:<math> | :<math>r_{BE}=\frac{u_{BE}}{i_B}\bigg|_{u_{CE}=0}=\frac{\Delta U_{BE}}{\Delta I_B}\bigg|_{U_{CE}=const </math> | ||
Dla obwodu wyjściowego wyznacza się rodzinę charakterystyk wyjściowych. Jest to zależność <math>I_C = f(U_{CE})</math> przy <math>I_B = const.</math> | Dla obwodu wyjściowego wyznacza się rodzinę charakterystyk wyjściowych. Jest to zależność <math>I_C = f(U_{CE})</math> przy <math>I_B = const.</math> | ||
| Linia 668: | Linia 668: | ||
Z charakterystyki wyjściowej można wyznaczyć dynamiczną rezystancję wyjściową tranzystora <math>r_{CE}</math> | Z charakterystyki wyjściowej można wyznaczyć dynamiczną rezystancję wyjściową tranzystora <math>r_{CE}</math> | ||
:<math> | :<math>r_{CE}=\frac{u_{CE}}{i_C}\bigg|_{i_B=0}=\frac{\Delta U_{CE}}{\Delta I_C}\bigg|_{I_B=const </math> | ||
Zależność <math>I_C = f(I_B)</math> przy </math>U_{CE} = const</math> przedstawia charakterystykę przejściową tranzystora. Z tej charakterystyki można wyznaczyć statyczny i dynamiczny współczynnik wzmocnienia prądowego. | Zależność <math>I_C = f(I_B)</math> przy </math>U_{CE} = const</math> przedstawia charakterystykę przejściową tranzystora. Z tej charakterystyki można wyznaczyć statyczny i dynamiczny współczynnik wzmocnienia prądowego. | ||
| Linia 711: | Linia 711: | ||
|valign="top"|Wpływ temperatury na parametry tranzystora. Prądy zerowe w tranzystorze bipolarnym rosną wraz z temperaturą <math>T_j\,</math> struktury półprzewodnikowej | |valign="top"|Wpływ temperatury na parametry tranzystora. Prądy zerowe w tranzystorze bipolarnym rosną wraz z temperaturą <math>T_j\,</math> struktury półprzewodnikowej | ||
:<math>I_{CB0}(T)=I_{CB0}(T_j)\cdot e^{ | :<math>I_{CB0}(T)=I_{CB0}(T_j)\cdot e^{b\cdot (T-T_j)}</math> | ||
gdzie b = 0,07 dla Ge, b = 0,12 dla Si | gdzie b = 0,07 dla Ge, b = 0,12 dla Si | ||
| Linia 719: | Linia 719: | ||
dla germany | dla germany | ||
:<math>I_{CB0}(T)=I_{CB0}(T_j)\cdot 2^{ | :<math>I_{CB0}(T)=I_{CB0}(T_j)\cdot 2^{\frac{(T-T_j)}{6}}</math> | ||
lub dla krzemu | lub dla krzemu | ||
:<math>I_{CB0}(T)=I_{CB0}(T_j)\cdot 2^{ | :<math>I_{CB0}(T)=I_{CB0}(T_j)\cdot 2^{\frac{(T-T_j)}{10}}</math> | ||
Także napięcie na złączu baza-emiter zmienia się w funkcji temperatury. Współczynnik temperaturowy tego napięcia jest ujemny (napięcie maleje ze wzrostem temperatury) i ma wartość 2,3 mV/ K. | Także napięcie na złączu baza-emiter zmienia się w funkcji temperatury. Współczynnik temperaturowy tego napięcia jest ujemny (napięcie maleje ze wzrostem temperatury) i ma wartość 2,3 mV/ K. | ||
Wersja z 08:58, 28 sie 2023
 |
Podstawowe elementy półprzewodnikowe |
 |
Elementy jednozłączowe
Wyróżnia się: Złącza półprzewodnikowe Złącza metal-półprzewodnik |
Literatura
M. P. Kaźmierkowski, J. T. Matysik: Wprowadzenie do elektroniki i energoelektroniki, Oficyna Wydawnicza PW, Warszawa 2005
J. Jaczewski, A. Opolski, J. Stolz: Podstawy elektroniki i energoelektroniki, WNT, Warszawa 1981
P. E. Gray, C. L. Searle: Podstawy elektroniki, PWN, Warszawa 1976