PF Moduł 14: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „ \displaystyle ” na „” |
m Zastępowanie tekstu – „\displaystyle ” na „” |
||
| Linia 29: | Linia 29: | ||
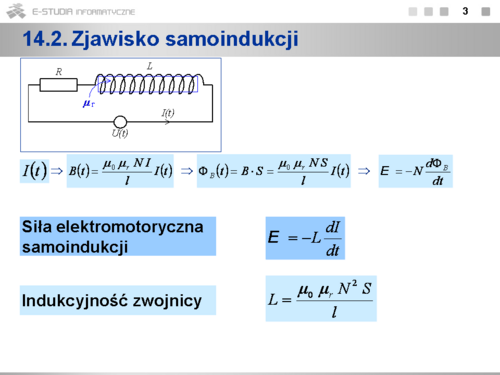
Jeśli natężenie prądu płynącego w zwojnicy zmienia się w czasie <math>I(t)\,</math> , to funkcją czasu jest również wektor indukcji pola magnetycznego wytwarzanego przez ten prąd wewnątrz zwojnicy <math>B(t)\,</math> oraz wartość strumienia magnetycznego przez powierzchnię każdego zwoju <math>\Phi_B\,</math> , a więc w zwojach powstają jednakowe i zgodne siły elektromotoryczne o wartości | Jeśli natężenie prądu płynącego w zwojnicy zmienia się w czasie <math>I(t)\,</math> , to funkcją czasu jest również wektor indukcji pola magnetycznego wytwarzanego przez ten prąd wewnątrz zwojnicy <math>B(t)\,</math> oraz wartość strumienia magnetycznego przez powierzchnię każdego zwoju <math>\Phi_B\,</math> , a więc w zwojach powstają jednakowe i zgodne siły elektromotoryczne o wartości | ||
:<math> | :<math>E_z=-\frac{d\Phi_B}{dt}</math> | ||
Zatem całkowita siła elektromotoryczna powstająca w zwojnicy jest równa | Zatem całkowita siła elektromotoryczna powstająca w zwojnicy jest równa | ||
| Linia 51: | Linia 51: | ||
Pomnóżmy równanie opisujące przepływ prądu w obwodzie przez <math>I\,</math> | Pomnóżmy równanie opisujące przepływ prądu w obwodzie przez <math>I\,</math> | ||
:<math> | :<math>U_0I=LI\frac{dI}{dt}+RI^2</math> | ||
Iloczyn natężenia prądu i napięcia źródła <math>U_0I=P</math> to moc źródła | Iloczyn natężenia prądu i napięcia źródła <math>U_0I=P</math> to moc źródła | ||
| Linia 57: | Linia 57: | ||
Składnik <math>RI^2=P_R</math> to moc w oporniku. | Składnik <math>RI^2=P_R</math> to moc w oporniku. | ||
Zatem wyrażenie <math> | Zatem wyrażenie <math>LI\frac{dI}{dt}=P_B=\frac{dW_B}{dt}</math> to moc w zwojnicy, czyli szybkość zmiany energii pola magnetycznego we wnętrzu zwojnicy. | ||
Po scałkowaniu otrzymujemy wzór określający energię pola magnetycznego <math>W_B\,</math> wewnątrz zwojnicy | Po scałkowaniu otrzymujemy wzór określający energię pola magnetycznego <math>W_B\,</math> wewnątrz zwojnicy | ||
| Linia 63: | Linia 63: | ||
Wykorzystując wzory | Wykorzystując wzory | ||
:<math> | :<math>L=\frac{\mu_0 \mu_r N^2 S}{l}</math> | ||
:<math> | :<math>B=\frac{\mu_0 \mu_r N}{l}I</math> | ||
otrzymamy zależność energii pola magnetycznego od wartości wektora indukcji magnetycznej gdzie <math>V\,</math> jest objętością, oraz wzór określający przestrzenną gęstość energii pola magnetycznego | otrzymamy zależność energii pola magnetycznego od wartości wektora indukcji magnetycznej gdzie <math>V\,</math> jest objętością, oraz wzór określający przestrzenną gęstość energii pola magnetycznego | ||
| Linia 95: | Linia 95: | ||
Przejdźmy teraz do rozważań energetycznych. Iloczyn napięcia i natężenia prądu jest równy mocy, a zatem możemy obliczyć moc <math>P_E\,</math> i energię <math>W_E\,</math> pola elektrycznego w kondensatorze | Przejdźmy teraz do rozważań energetycznych. Iloczyn napięcia i natężenia prądu jest równy mocy, a zatem możemy obliczyć moc <math>P_E\,</math> i energię <math>W_E\,</math> pola elektrycznego w kondensatorze | ||
:<math> | :<math>P_E=\frac{W_E}{dt}=U_C I=\frac{q}{C}\cdot I</math> | ||
:<math> | :<math>W_E=\int \frac{q}{C}dq=\frac{1}{2C}\cdot q^2=\frac{1}{2C}\cdot q_{0}^2cos^2\omega_0 t</math> | ||
oraz moc <math>P_B\,</math> i energię <math>W_B\,</math> pola magnetycznego w zwojnicy | oraz moc <math>P_B\,</math> i energię <math>W_B\,</math> pola magnetycznego w zwojnicy | ||
:<math> | :<math>P_B=\frac{W_B}{dt}=U_L I=L\frac{dI}{dt}\cdot I</math> | ||
:<math> | :<math>W_B=\int LIdI=\frac{1}{2}LI^2=\frac{1}{2C}\cdot q_{0}^2sin^2\omega_0 t</math> | ||
Jak widać energie pól w kondensatorze i w zwojnicy mają takie same amplitudy, ale są przesunięte w fazie o <math>\pi/2\,</math>. Całkowita energia układu drgającego będąca sumą energii pola elektrycznego w kondensatorze i pola magnetycznego w zwojnicy | Jak widać energie pól w kondensatorze i w zwojnicy mają takie same amplitudy, ale są przesunięte w fazie o <math>\pi/2\,</math>. Całkowita energia układu drgającego będąca sumą energii pola elektrycznego w kondensatorze i pola magnetycznego w zwojnicy | ||
| Linia 155: | Linia 155: | ||
Amplitudę drgań i przesunięcie fazowe w stanie rezonansu można wyrazić wzorami: | Amplitudę drgań i przesunięcie fazowe w stanie rezonansu można wyrazić wzorami: | ||
:<math> | :<math>(q_0)_{max}=\frac{U_0/L}{2\beta \sqrt{\omega_{0}^2-\beta^2}}</math> | ||
:<math> | :<math>\varphi_r=arctg\frac{\sqrt{\omega_{0}^2-\beta^2}}{\beta}</math> | ||
Szczególny przypadek rezonansu występuje w przypadku gdy współczynnik tłumienia <math>\beta = 0</math>. Dla takiego układu rezonans zachodzi przy częstości wymuszania równej częstości drgań własnych <math>\omega_r=\omega_0</math> i objawia się wzrostem amplitudy do nieskończoności oraz przesunięciem fazowym <math>\omega_r=\pi/2</math>. W takiej sytuacji dochodzi przeważnie do zniszczenia układu drgającego zanim amplituda drgań osiągnie wartość nieskończoną. | Szczególny przypadek rezonansu występuje w przypadku gdy współczynnik tłumienia <math>\beta = 0</math>. Dla takiego układu rezonans zachodzi przy częstości wymuszania równej częstości drgań własnych <math>\omega_r=\omega_0</math> i objawia się wzrostem amplitudy do nieskończoności oraz przesunięciem fazowym <math>\omega_r=\pi/2</math>. W takiej sytuacji dochodzi przeważnie do zniszczenia układu drgającego zanim amplituda drgań osiągnie wartość nieskończoną. | ||
| Linia 173: | Linia 173: | ||
Wzory opisujące drgania wymuszone i rezonans można zapisać w uniwersalnej postaci bezwymiarowej, słusznej zarówno dla drgań elektromagnetycznych, jak i dla drgań mechanicznych. W tym celu wprowadza się tzw. '''parametry zredukowane''': | Wzory opisujące drgania wymuszone i rezonans można zapisać w uniwersalnej postaci bezwymiarowej, słusznej zarówno dla drgań elektromagnetycznych, jak i dla drgań mechanicznych. W tym celu wprowadza się tzw. '''parametry zredukowane''': | ||
zredukowany współczynnik tłumienia <math> | zredukowany współczynnik tłumienia <math>u=\frac{\beta}{\omega_0}</math> | ||
zredukowana częstość drgań <math> | zredukowana częstość drgań <math>w=\frac{\omega}{\omega_0}</math> | ||
zredukowana amplituda drgań wymuszonych <math> | zredukowana amplituda drgań wymuszonych <math>X=\frac{q_0(\omega)}{q_0(\omega \to 0)}=\frac{q_0(\omega)}{U_0 C}</math> | ||
Po zastosowaniu powyższych podstawień wzory określające: amplitudę drgań i przesunięcie fazowe dla dowolnej częstości wymuszania, częstość rezonansową oraz amplitudę drgań i przesunięcie fazowe w stanie rezonansu przyjmą postać: | Po zastosowaniu powyższych podstawień wzory określające: amplitudę drgań i przesunięcie fazowe dla dowolnej częstości wymuszania, częstość rezonansową oraz amplitudę drgań i przesunięcie fazowe w stanie rezonansu przyjmą postać: | ||
| Linia 183: | Linia 183: | ||
<math>\begin{matrix}X=\frac{1}{\sqrt{(1-w^2)^2}+4u^2w^2} &\varphi=arctg\frac{2uw}{1-w^2} \end{matrix}</math> | <math>\begin{matrix}X=\frac{1}{\sqrt{(1-w^2)^2}+4u^2w^2} &\varphi=arctg\frac{2uw}{1-w^2} \end{matrix}</math> | ||
:<math> | :<math>w_r=\sqrt{1-2u^2}</math> | ||
Na slajdzie przedstawiono wykresy zależności zredukowanej amplitudy drgań <math>X\,</math> od zredukowanej częstości drgań w dla kilku wartości zredukowanego współczynnika tłumienia <math>u\,</math>. W miarę wzrostu współczynnika tłumienia rezonans pojawia się dla częstości coraz mniejszych i wartość amplitudy drgań w stanie rezonansu jest coraz mniejsza. Po przekroczeniu granicznej wartości współczynnika tłumienia rezonans nie pojawia się (krzywa <math>X(w)\,</math> nie posiada maksimum). | Na slajdzie przedstawiono wykresy zależności zredukowanej amplitudy drgań <math>X\,</math> od zredukowanej częstości drgań w dla kilku wartości zredukowanego współczynnika tłumienia <math>u\,</math>. W miarę wzrostu współczynnika tłumienia rezonans pojawia się dla częstości coraz mniejszych i wartość amplitudy drgań w stanie rezonansu jest coraz mniejsza. Po przekroczeniu granicznej wartości współczynnika tłumienia rezonans nie pojawia się (krzywa <math>X(w)\,</math> nie posiada maksimum). | ||
| Linia 205: | Linia 205: | ||
Całkowity strumień wektora indukcji pola elektrycznego przez zamknietą powierzchnię jest równy ładunkowi zawartemu w otoczonej przez tę powierzchnię objętości. Pole elektryczne jest polem źródłowym - źródłem pola elektrycznego jest ładunek elektryczny. | Całkowity strumień wektora indukcji pola elektrycznego przez zamknietą powierzchnię jest równy ładunkowi zawartemu w otoczonej przez tę powierzchnię objętości. Pole elektryczne jest polem źródłowym - źródłem pola elektrycznego jest ładunek elektryczny. | ||
Ze wzoru wyrażającego w postaci całkowej związek między natężeniem pola i potencjałem wynika, że w polu elektrycznym wytworzonym przez ładunki <math> | Ze wzoru wyrażającego w postaci całkowej związek między natężeniem pola i potencjałem wynika, że w polu elektrycznym wytworzonym przez ładunki <math>\oint_{L} \overrightarrow{E}\ d\overrightarrow{l}=0</math> , a więc pole wytworzone przez ładunki jest polem bezwirowym (linie sił pola mają początek i koniec). | ||
*Prawo Gaussa dla pola magnetycznego | *Prawo Gaussa dla pola magnetycznego | ||
:<math> | :<math>\oint_{S} \overrightarrow{B}\cdot d\overrightarrow{S}=0</math> | ||
Całkowity strumień wektora indukcji pola magnetycznego przez zamknietą powierzchnię jest równy zeru. Pole magnetyczne jest polem bezźródłowym. Nie istnieją monopole magnetyczne. | Całkowity strumień wektora indukcji pola magnetycznego przez zamknietą powierzchnię jest równy zeru. Pole magnetyczne jest polem bezźródłowym. Nie istnieją monopole magnetyczne. | ||
| Linia 217: | Linia 217: | ||
Cyrkulacja wektora natężenia pola elektrycznego wzdłuż zamkniętej krzywej <math>L\,</math> jest równa szybkości zmiany (ze znakiem ujemnym) strumienia wektora indukcji pola magnetycznego przez powierzchnię <math>S\,</math>, ograniczoną przez krzywą <math>L\,</math>. Wir pola elektrycznego jest powiązany z wektorową zmianą pola magnetycznego za pomocą reguły śruby prawoskrętnej, z uwzględnieniem znaku minus po prawej stronie równania. | Cyrkulacja wektora natężenia pola elektrycznego wzdłuż zamkniętej krzywej <math>L\,</math> jest równa szybkości zmiany (ze znakiem ujemnym) strumienia wektora indukcji pola magnetycznego przez powierzchnię <math>S\,</math>, ograniczoną przez krzywą <math>L\,</math>. Wir pola elektrycznego jest powiązany z wektorową zmianą pola magnetycznego za pomocą reguły śruby prawoskrętnej, z uwzględnieniem znaku minus po prawej stronie równania. | ||
Wskutek zmiany strumienia pola magnetycznego powstaje wirowe pole elektryczne (linie sił pola są krzywymi zamkniętymi). Takie pole elektryczne jest polem bezźródłowym, tzn. w takim polu strumień wektora indukcji elektrycznej przez zamknietą powierzchnię jest równy zeru <math> | Wskutek zmiany strumienia pola magnetycznego powstaje wirowe pole elektryczne (linie sił pola są krzywymi zamkniętymi). Takie pole elektryczne jest polem bezźródłowym, tzn. w takim polu strumień wektora indukcji elektrycznej przez zamknietą powierzchnię jest równy zeru <math>\oint_{S} \overrightarrow{D}\ d\overrightarrow{S}=0</math>. | ||
*II prawo Maxwella (uogólnione prawo Ampere’a) - wirowe pole magnetyczne | *II prawo Maxwella (uogólnione prawo Ampere’a) - wirowe pole magnetyczne | ||
| Linia 223: | Linia 223: | ||
Cyrkulacja wektora natężenia pola magnetycznego wzdłuż zamkniętej krzywej <math>L\,</math> jest równa sumie natężenia prądu przepływającego przez powierzchnię <math>S\,</math>, ograniczoną przez krzywą <math>L\,</math> oraz szybkości zmiany strumienia wektora indukcji pola elektrycznego przez powierzchnię <math>S\,</math>, ograniczoną przez tę krzywą, czyli natężenia tzw. prądu przesunięcia. | Cyrkulacja wektora natężenia pola magnetycznego wzdłuż zamkniętej krzywej <math>L\,</math> jest równa sumie natężenia prądu przepływającego przez powierzchnię <math>S\,</math>, ograniczoną przez krzywą <math>L\,</math> oraz szybkości zmiany strumienia wektora indukcji pola elektrycznego przez powierzchnię <math>S\,</math>, ograniczoną przez tę krzywą, czyli natężenia tzw. prądu przesunięcia. | ||
:<math> | :<math>\oint_{L} \overrightarrow{D}\cdot d\overrightarrow{l}=\int_{S} \overrightarrow{j}\cdot d\overrightarrow{S}+\frac{\partial}{\partial t}\int_{S}\overrightarrow{D}\cdot d\overrightarrow{S}</math> | ||
Wir pola magnetycznego jest powiązany z wektorem gęstości prądu oraz z wektorową zmianą pola elektrycznego za pomocą reguły śruby prawoskrętnej. | Wir pola magnetycznego jest powiązany z wektorem gęstości prądu oraz z wektorową zmianą pola elektrycznego za pomocą reguły śruby prawoskrętnej. | ||
| Linia 245: | Linia 245: | ||
Kartezjański układ wspórzędnych w przestrzeni trójwymiarowej | Kartezjański układ wspórzędnych w przestrzeni trójwymiarowej | ||
Pole wektorowe - każdemu punktowi przestrzeni jest przyporządkowany wektor <math> | Pole wektorowe - każdemu punktowi przestrzeni jest przyporządkowany wektor <math>\overrightarrow{a}=[a_x, a_y, a_z]</math> | ||
Pole skalarne - każdemu punktowi przestrzeni jest przyporządkowana skalarna funkcja <math> | Pole skalarne - każdemu punktowi przestrzeni jest przyporządkowana skalarna funkcja <math>f(x,y,z)</math> | ||
*operator nabla <math> | *operator nabla <math>\nabla=\left[\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z} \right]</math> | ||
*gradient pola skalarnego <math> | *gradient pola skalarnego <math>\nabla f=\left[\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right]\equiv grad\, f</math> | ||
:operator nabla działa na funkcję skalarną | :operator nabla działa na funkcję skalarną | ||
*dywergencja pola wektorowego <math> | *dywergencja pola wektorowego <math>\nabla \overrightarrow{a}=\frac{\partial a_x}{\partial x}+ \frac{\partial a_y}{\partial y}+ \frac{\partial a_z}{\partial z}\equiv div\, \overrightarrow{a}</math> | ||
:iloczyn skalarny operatora nabla i wektora | :iloczyn skalarny operatora nabla i wektora | ||
*rotacja pola wektorowego <math> | *rotacja pola wektorowego <math>\nabla \times \overrightarrow{a}=\left[\frac{\partial a_z}{\partial y}-\frac{\partial a_y}{\partial z},\, \frac{\partial a_x}{\partial z}-\frac{\partial a_z}{\partial x},\, \frac{\partial a_y}{\partial x}-\frac{\partial a_x}{\partial y}\right]\equiv div\, \overrightarrow{a}</math> | ||
:iloczyn wektorowy operatora nabla i wektora | :iloczyn wektorowy operatora nabla i wektora | ||
*laplasjan <math> | *laplasjan <math>\Delta =\nabla \cdot \nabla=\frac{\partial^2}{\partial x^2}+ \frac{\partial^2}{\partial y^2}+ \frac{\partial^2}{\partial z^2} </math> | ||
:iloczyn skalarny operatorów nabla | :iloczyn skalarny operatorów nabla | ||
*twierdzenie dla gradientów <math> | *twierdzenie dla gradientów <math>\int_{P_1}^{P_2} (\nabla f)\cdot d\overrightarrow{l}=f(P_1)-f(P_2)</math> | ||
*twierdzenie Gaussa (dla dywergencji) <math> | *twierdzenie Gaussa (dla dywergencji) <math>\int_{S} \overrightarrow{a}\cdot d\overrightarrow{S}=\int_{V} (\nabla \overrightarrow{a})dV=\int_{V} (div\, \overrightarrow{a})dV</math> | ||
*twierdzenie Stokesa (dla rotacji) <math> | *twierdzenie Stokesa (dla rotacji) <math>\int_{L} \overrightarrow{a}\cdot d\overrightarrow{l}=\int_{S} (\nabla \times \overrightarrow{a})d\overrightarrow{S}=\int_{S} (rot\, \overrightarrow{a})dS</math> | ||
|} | |} | ||
| Linia 303: | Linia 303: | ||
'''Przykład 14.1''' | '''Przykład 14.1''' | ||
Przewodzący pręt o długości <math>l\,</math> wiruje z prędkością kątową <math> | Przewodzący pręt o długości <math>l\,</math> wiruje z prędkością kątową <math>\overrightarrow{\omega}=[0, \omega, 0]</math> wokół osi OY prostopadłej do pręta i przechodzącej przez jego koniec, w stałym, jednorodnym polu magnetycznym o wektorze indukcji <math>\overrightarrow{B}=[0, 0, -B]</math> . | ||
Obliczyć wartość napięcia między końcami pręta i określić jego polaryzację. | Obliczyć wartość napięcia między końcami pręta i określić jego polaryzację. | ||
| Linia 316: | Linia 316: | ||
''Metoda 1'' | ''Metoda 1'' | ||
Na elektrony w poruszającym się pręcie pole magnetyczne działa siłą <math> | Na elektrony w poruszającym się pręcie pole magnetyczne działa siłą <math>\overrightarrow{F}_m</math> | ||
:<math> | :<math>\overrightarrow{F}_m=-e\overrightarrow{v}\times\overrightarrow{B}</math> | ||
:<math> | :<math>\overrightarrow{v}=\overrightarrow{\omega}\times\overrightarrow{r}</math> | ||
:<math> | :<math>\overrightarrow{F}_m=-e(\overrightarrow{\omega}\times\overrightarrow{r})\times\overrightarrow{B}=e\overrightarrow{B}\times(\overrightarrow{\omega}\times\overrightarrow{r})=</math> | ||
::<math>=e\left[\overrightarrow{\omega}(\overrightarrow{B}\cdot\overrightarrow{r})-\overrightarrow{r}(\overrightarrow{B}\cdot\overrightarrow{\omega})\right]=-eB\omega\overrightarrow{r}</math> | ::<math>=e\left[\overrightarrow{\omega}(\overrightarrow{B}\cdot\overrightarrow{r})-\overrightarrow{r}(\overrightarrow{B}\cdot\overrightarrow{\omega})\right]=-eB\omega\overrightarrow{r}</math> | ||
która jest skierowana wzdłuż pręta w stronę punktu O. Wskutek przemieszczenia części elektronów w kierunku punktu O w pręcie powstaje pole elektryczne o natężeniu <math> | która jest skierowana wzdłuż pręta w stronę punktu O. Wskutek przemieszczenia części elektronów w kierunku punktu O w pręcie powstaje pole elektryczne o natężeniu <math>\overrightarrow{F}_e=-e\overrightarrow{E}</math> , które na elektrony działa siłą | ||
Przemieszczanie elektronów ustaje, gdy w pręcie zostanie wytworzone pole elektryczne o takim natężeniu, że siły te zrównają się | Przemieszczanie elektronów ustaje, gdy w pręcie zostanie wytworzone pole elektryczne o takim natężeniu, że siły te zrównają się | ||
| Linia 347: | Linia 347: | ||
W układzie odniesienia związanym z wirującym prętem (nieinercjalny układ odniesienia) na elektrony działa siła bezwładności, która stara się przesunąć elektrony w kierunku końca pręta | W układzie odniesienia związanym z wirującym prętem (nieinercjalny układ odniesienia) na elektrony działa siła bezwładności, która stara się przesunąć elektrony w kierunku końca pręta | ||
:<math> | :<math>\overrightarrow{F}_b=m\omega^2 \overrightarrow{r}</math> | ||
Zrównanie się tej siły z siłą, jaką działa pole magnetyczne spowoduje, że napięcie między końcami pręta będzie równe zeru | Zrównanie się tej siły z siłą, jaką działa pole magnetyczne spowoduje, że napięcie między końcami pręta będzie równe zeru | ||
| Linia 355: | Linia 355: | ||
Jak widać może to nastąpić przy częstości równej częstości cyklotronowej dla elektronu w polu o danej wartości wektora indukcji, która w tym przypadku jest równa | Jak widać może to nastąpić przy częstości równej częstości cyklotronowej dla elektronu w polu o danej wartości wektora indukcji, która w tym przypadku jest równa | ||
:<math> | :<math>\omega_c=1,76\cdot 10^{11}s^{-1}</math> | ||
Jak widać może to nastąpić przy częstości równej częstości cyklotronowej dla elektronu w polu o danej wartości wektora indukcji, która w tym przypadku jest równa | Jak widać może to nastąpić przy częstości równej częstości cyklotronowej dla elektronu w polu o danej wartości wektora indukcji, która w tym przypadku jest równa | ||
:<math> | :<math>v_k=\omega l=1,76\cdot 10^{11}m/s>c</math> | ||
większą od prędkości światła w próżni, co jak wiadomo nie jest możliwe. | większą od prędkości światła w próżni, co jak wiadomo nie jest możliwe. | ||
| Linia 371: | Linia 371: | ||
'''Przykład 14.2''' | '''Przykład 14.2''' | ||
Do obwodu o oporze R, indukcyjności L i pojemności C dołączono źródło napięcia <math> | Do obwodu o oporze R, indukcyjności L i pojemności C dołączono źródło napięcia <math>U(t)=U_0 sin\omega t</math> . Znaleźć zależność od czasu napięcia na kondensatorze, natężenia prądu, napięcia na oporniku oraz napięcia na zwojnicy. | ||
| Linia 380: | Linia 380: | ||
'''Napięcie na kondensatorze''' | '''Napięcie na kondensatorze''' | ||
:<math> | :<math>U_C(t)=\frac{q(t)}{C}=U(t)=U_{C0} sin(\omega t-\varphi)</math> | ||
:<math>\begin{matrix}U_{C0}=U_0\frac{\omega_{0}^2}{\sqrt{(\omega_{0}^2-\omega^2)^2}+4\beta^2\omega^2}; &\varphi=arctg\frac{2\beta \omega}{\omega_{0}^2-\omega^2} \end{matrix}</math> | :<math>\begin{matrix}U_{C0}=U_0\frac{\omega_{0}^2}{\sqrt{(\omega_{0}^2-\omega^2)^2}+4\beta^2\omega^2}; &\varphi=arctg\frac{2\beta \omega}{\omega_{0}^2-\omega^2} \end{matrix}</math> | ||
| Linia 392: | Linia 392: | ||
a przesunięcie fazowe względem napięcia wymuszającego wynosi | a przesunięcie fazowe względem napięcia wymuszającego wynosi | ||
:<math> | :<math>\varphi_r=arctg\frac{\sqrt{\omega_{0}^2-\beta^2}}{\beta}=arctg\frac{\omega_r}{\beta}</math> | ||
Wartości graniczne: gdy częstość wymuszania dąży do zera, to amplituda napięcia na kondensatorze dąży do wartości <math>U_0\,</math> , zaś dla częstości znacznie większych od częstości własnej <math>\omega_0\,</math> dąży do zera. Przesunięcie fazowe zmienia się od zera dla bardzo małej częstości wymuszania do <math>\pi\,</math> dla częstości bardzo dużej. | Wartości graniczne: gdy częstość wymuszania dąży do zera, to amplituda napięcia na kondensatorze dąży do wartości <math>U_0\,</math> , zaś dla częstości znacznie większych od częstości własnej <math>\omega_0\,</math> dąży do zera. Przesunięcie fazowe zmienia się od zera dla bardzo małej częstości wymuszania do <math>\pi\,</math> dla częstości bardzo dużej. | ||
| Linia 398: | Linia 398: | ||
'''Natężenie prądu''' | '''Natężenie prądu''' | ||
:<math> | :<math>I(t)=\frac{dq}{dt}=I_0sin(\omega t -\varphi_R)</math> | ||
:<math>\begin{matrix}I_0=\frac{U_0}{L}\frac{\omega}{\sqrt{(\omega_{0}^2-\omega^2)^2}+4\beta^2\omega^2}; &\varphi_R=arctg\frac{\omega^2-\omega_{0}^2}{2\beta \omega} \end{matrix}</math> | :<math>\begin{matrix}I_0=\frac{U_0}{L}\frac{\omega}{\sqrt{(\omega_{0}^2-\omega^2)^2}+4\beta^2\omega^2}; &\varphi_R=arctg\frac{\omega^2-\omega_{0}^2}{2\beta \omega} \end{matrix}</math> | ||
| Linia 408: | Linia 408: | ||
'''Napięcie na oporniku''' | '''Napięcie na oporniku''' | ||
:<math> | :<math>U_R(t)=R\cdot I(t)=U_{R0}sin(\omega t -\varphi_R)</math> | ||
:<math>\begin{matrix}U_{R0}=R\cdot I_0=U_0\frac{2\beta\omega}{\sqrt{(\omega_{0}^2-\omega^2)^2}+4\beta^2\omega^2}; &\varphi_R=arctg\frac{\omega^2-\omega_{0}^2}{2\beta \omega} \end{matrix}</math> | :<math>\begin{matrix}U_{R0}=R\cdot I_0=U_0\frac{2\beta\omega}{\sqrt{(\omega_{0}^2-\omega^2)^2}+4\beta^2\omega^2}; &\varphi_R=arctg\frac{\omega^2-\omega_{0}^2}{2\beta \omega} \end{matrix}</math> | ||
| Linia 420: | Linia 420: | ||
'''Napięcie na zwojnicy''' | '''Napięcie na zwojnicy''' | ||
:<math> | :<math>U_L(t)=L\frac{dI}{dt}=U_{L0}sin(\omega t -\varphi_L)</math> | ||
:<math>\begin{matrix}U_{L0}=U_0\frac{\omega^2}{\sqrt{(\omega_{0}^2-\omega^2)^2}+4\beta^2\omega^2}; &\varphi_L=arctg\frac{2\beta \omega}{\omega_{0}^2-\omega^2}-\pi \end{matrix}</math> | :<math>\begin{matrix}U_{L0}=U_0\frac{\omega^2}{\sqrt{(\omega_{0}^2-\omega^2)^2}+4\beta^2\omega^2}; &\varphi_L=arctg\frac{2\beta \omega}{\omega_{0}^2-\omega^2}-\pi \end{matrix}</math> | ||
| Linia 430: | Linia 430: | ||
a przesunięcie fazowe względem napięcia wymuszającego wynosi wtedy | a przesunięcie fazowe względem napięcia wymuszającego wynosi wtedy | ||
:<math> | :<math>\varphi_L=arctg\left(-\frac{\sqrt{\omega_{0}^2-\beta^2}}{\beta}\right)-\pi=arctg\left(-\frac{\omega_r}{\beta}\right)-\pi</math> | ||
Napięcie na zwojnicy ma fazę przeciwną względem napięcia na kondensatorze, zaś amplituda osiąga wartość największą dla częstości większej od częstości rezonansowej, a nawet większej od częstości własnej. Gdy współczynnik tłumienia zmienia się od zera do wartości granicznej to częstość ta rośnie od wartości <math>\omega_0\,</math> do nieskończoności. | Napięcie na zwojnicy ma fazę przeciwną względem napięcia na kondensatorze, zaś amplituda osiąga wartość największą dla częstości większej od częstości rezonansowej, a nawet większej od częstości własnej. Gdy współczynnik tłumienia zmienia się od zera do wartości granicznej to częstość ta rośnie od wartości <math>\omega_0\,</math> do nieskończoności. | ||
| Linia 452: | Linia 452: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowiedź </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowiedź </span><div class="mw-collapsible-content" style="display:none"> | ||
:'''a.''' <math> | :'''a.''' <math>U_1=\frac{mu_0Iv}{2\pi}ln\left(1+\frac{l}{d}\right)</math> | ||
:'''b.''' <math> | :'''b.''' <math>U_2=\frac{mu_0Iv}{2\pi}\cdot \frac{l}{d+vt}</math> | ||
W pierwszym przypadku napięcie ma stałą wartość (pręt porusza się tak, że średnia wartość wektora indukcji magnetycznej jest stała), natomiast w drugim przypadku napięcie maleje w miarę oddalania się od długiego przewodu(pręt przemieszcza się w obszary coraz słabszego pola). Zatem stosunek napięć jest zależny od czasu. | W pierwszym przypadku napięcie ma stałą wartość (pręt porusza się tak, że średnia wartość wektora indukcji magnetycznej jest stała), natomiast w drugim przypadku napięcie maleje w miarę oddalania się od długiego przewodu(pręt przemieszcza się w obszary coraz słabszego pola). Zatem stosunek napięć jest zależny od czasu. | ||
:<math> | :<math>\frac{U_1}{U_2}=\frac{d+vt}{l}ln\left(1+\frac{l}{d}\right) </math> | ||
</div></div> | </div></div> | ||
| Linia 475: | Linia 475: | ||
:[[Grafika:PF_M14_Zad_Rys2.png]] | :[[Grafika:PF_M14_Zad_Rys2.png]] | ||
:'''a.''' <math> | :'''a.''' <math>\Phi_B=2\cdot \frac{mu_0I}{4\pi}\left[\int_{a}^{2a}\left(\int_{a}^{2a} \frac{x}{y\sqrt{x^2+y^2}}dx+\int_{a}^{2a} \frac{dx}{y}\right)dy\right]=1,19\frac{mu_0 a}{2\pi}\cdot I</math> | ||
:'''b.''' <math> | :'''b.''' <math>Q=\int_{I}^{0} -1,19\frac{mu_0 a}{2\pi R}\cdot I=1,19\frac{mu_0 aI}{2\pi R}</math> | ||
Warto zauważyć, że wartość tego ładunku jest niezależna od rodzaju funkcji opisującej zanik prądu. | Warto zauważyć, że wartość tego ładunku jest niezależna od rodzaju funkcji opisującej zanik prądu. | ||
:'''c.''' <math> | :'''c.''' <math>W=\frac{1}{2R\tau}\left(1,19\frac{mu_0 I_0a}{2\pi} \right)^2</math> | ||
</div></div> | </div></div> | ||
| Linia 492: | Linia 492: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowiedź </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowiedź </span><div class="mw-collapsible-content" style="display:none"> | ||
:<math> | :<math>P=RI^2=\frac{B^2l^2v^2}{R}</math> | ||
</div></div> | </div></div> | ||
Wersja z 08:57, 28 sie 2023
Wykład
 |
Materiały do ćwiczeń
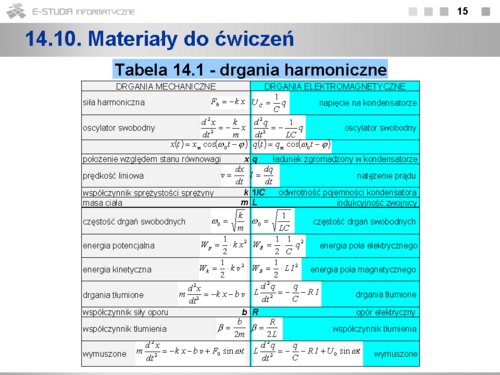
Drgania harmoniczne
Indukcja elektromagnetyczna
Przykład 14.1
Przewodzący pręt o długości wiruje z prędkością kątową wokół osi OY prostopadłej do pręta i przechodzącej przez jego koniec, w stałym, jednorodnym polu magnetycznym o wektorze indukcji .
Obliczyć wartość napięcia między końcami pręta i określić jego polaryzację.
Przyjąć, że , , .
Czy można tak dobrać wartość , aby w układzie odniesienia związanym z prętem konkurencja między siłą bezwładności i siłą jaką na elektrony działa pole magnetyczne spowodowała, że napięcie między końcami pręta będzie równe zeru?
Drgania elektromagnetyczne
Przykład 14.2
Do obwodu o oporze R, indukcyjności L i pojemności C dołączono źródło napięcia . Znaleźć zależność od czasu napięcia na kondensatorze, natężenia prądu, napięcia na oporniku oraz napięcia na zwojnicy.
Zadania
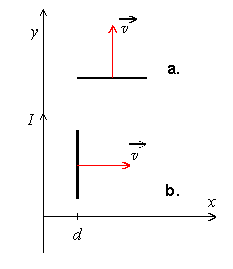
1. W polu magnetycznym wytworzonym wokół bardzo długiego, cienkiego przewodu prostoliniowego, w którym płynie prąd o natężeniu , porusza się ze stałą prędkością metalowy pręt o długości . Prędkość jest prostopadła do pręta. Obliczyć stosunek wartości napięcia między końcami pręta dla dwóch sposobów przesuwania pręta:
- a. wektor jest równoległy do przewodu
- b. wektor jest prostopadły do przewodu
Skomentować otrzymany wynik.
2. W odległości od nieskończenie długiego przewodu prostoliniowego w którym płynie prąd o natężeniu umieszczono kwadratowy obwód o boku i oporności . Obliczyć:
- a. Strumień pola magnetycznego przez powierzchnię obwodu.
- b. Ładunek jaki przepłynie w obwodzie po wyłączeniu prądu .
- c. Energię przekazaną do obwodu, przy założeniu, że zanik prądu ma charakter eksponencjalny, z czasem relaksacji .
3. Na długich poziomych szynach spiętych opornikiem o oporności leży pręt o masie i długości . Wektor indukcji stałego, jednorodnego pola magnetycznego jest skierowany przeciwnie do wektora natężenia pola grawitacyjnego . Obliczyć moc potrzebną do przesuwania pręta ze stałą prędkością . Zaniedbać oporność szyn i pręta oraz tarcie pręta o szyny.
4. W obwodzie RLC zachodzą elektromagnetyczne drgania wymuszone pod wpływem napięcia . Obliczyć średnią moc pochłanianą przez obwód w ciągu jednego okresu drgań. Dla jakiej wartości częstości wymuszania wartość tej mocy jest największa?