PEE Moduł 6: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 63: | Linia 63: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd6.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd6.png]] | ||
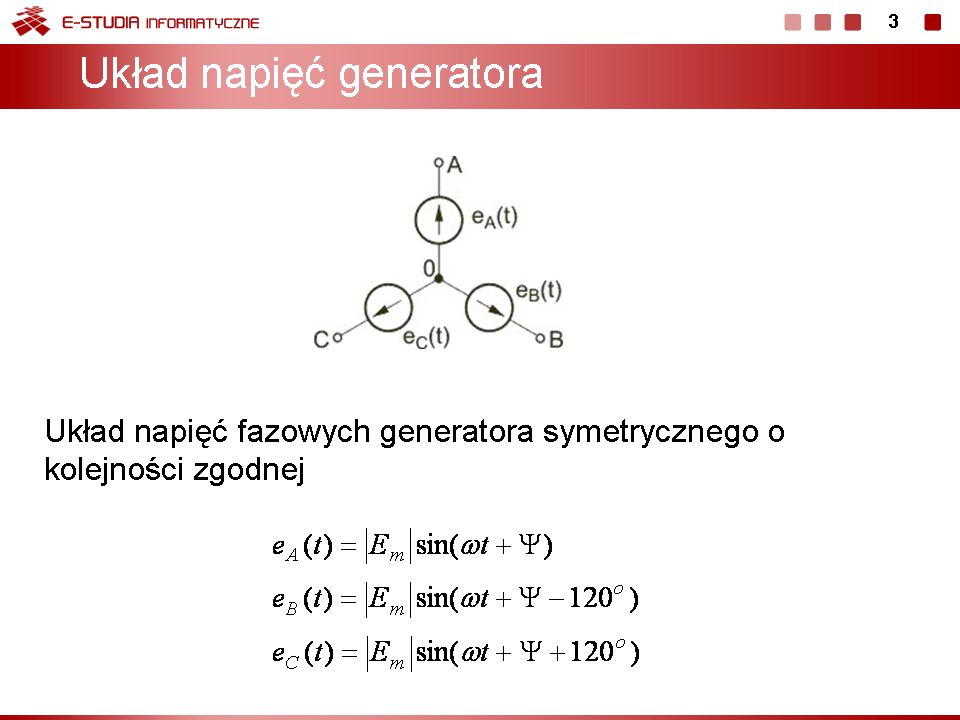
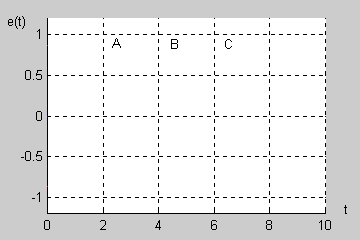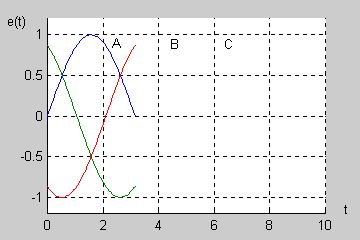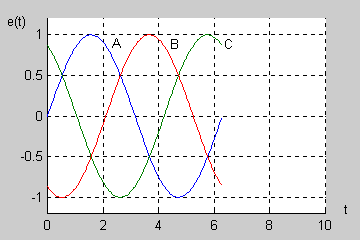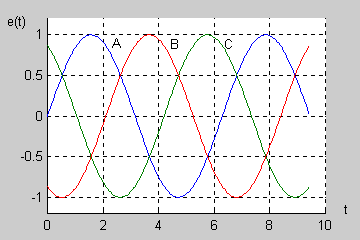
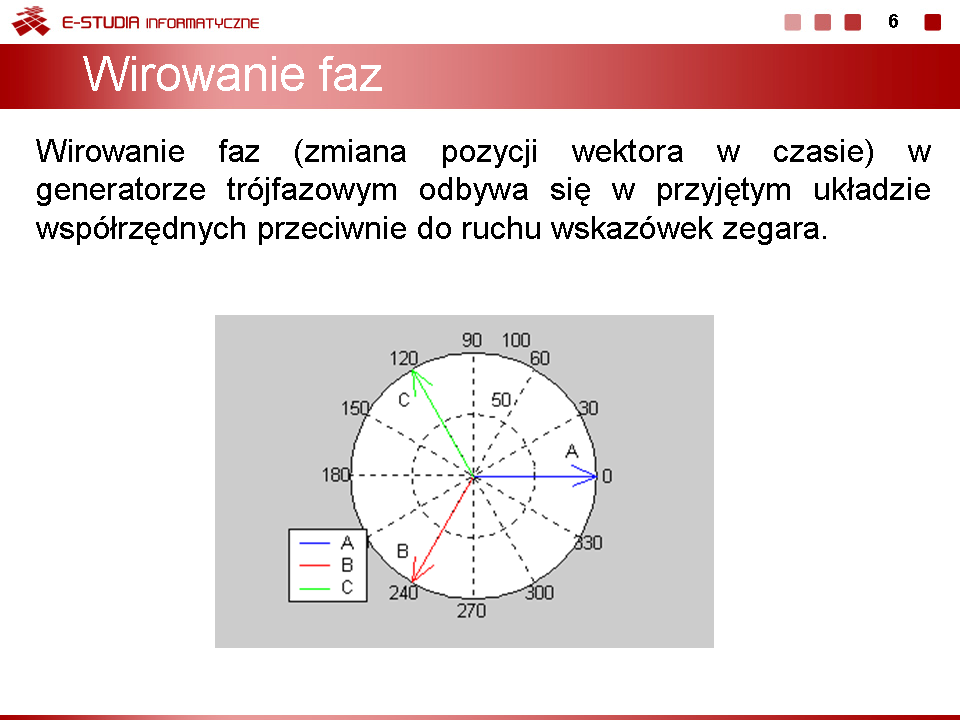
|valign="top"| | |valign="top"|Wirowanie faz (zmiana pozycji wektora w czasie) w generatorze trójfazowym odbywa się w przyjętym układzie współrzędnych przeciwnie do ruchu wskazówek zegara. | ||
[[Grafika:PEE_M6_anim_2.gif]] | |||
Rysunek powyżej pokazuje wektory napięć generatora trójfazowego wirujące w czasie. Wektory fazy B i C nadążają za wektorem A, przy czym przesunięcia fazowe między nimi są stałe i równe dokładnie <math>120^\circ</math>. Ważną cechą trójfazowego generatora symetrycznego jest zerowanie się sumy napięć fazowych | |||
: <math>E_A+E_B+E_C=0</math> | |||
Wartość zerowa sumy wynika bezpośrednio z symetrii poszczególnych napięć. Mianowicie | |||
: <math>E_A+E_B+E_C=E_A+E_Ae^{-j120^\circ}+E_Ae^{j120^\circ}=</math> | |||
: <math>=E_A \left ( 1-0,5-j{\sqrt{3} \over 2}-0,5+j{\sqrt{3} \over 2} \right )=0</math> | |||
|} | |} | ||
| Linia 70: | Linia 81: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd7.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd7.png]] | ||
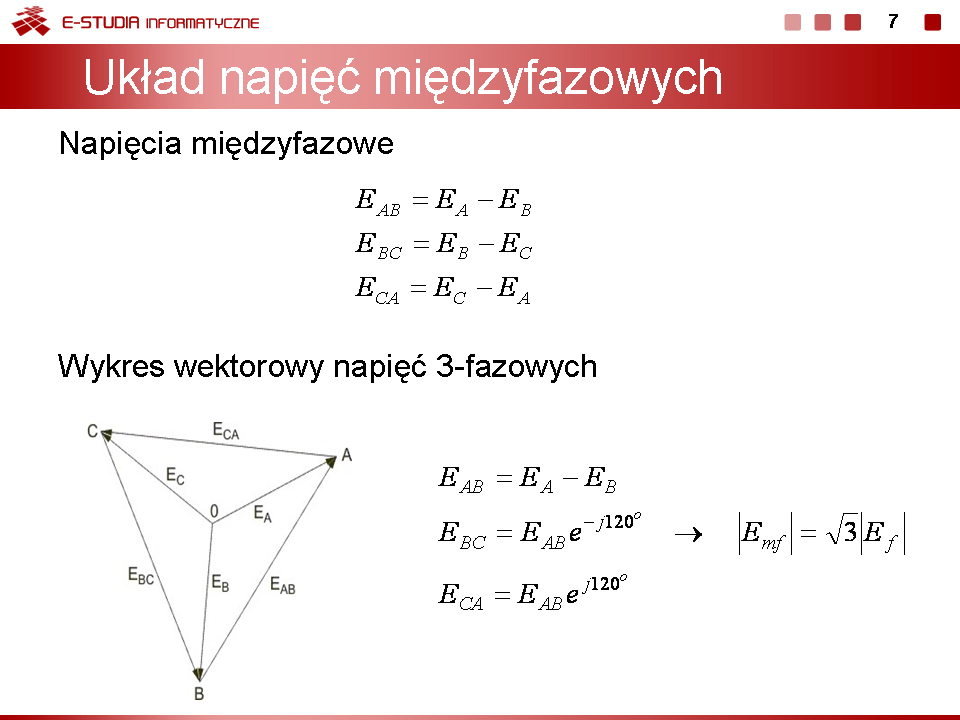
|valign="top"| | |valign="top"|'''Układ napięć międzyfazowych''' | ||
Oprócz napięć fazowych wyróżnia się układ '''napięć międzyfazowych''', zwanych również liniowymi, czyli napięć panujących między punktami zewnętrznymi poszczególnych faz. Przy trzech napięciach fazowych można wyróżnić trzy napięcia międzyfazowe: <math>E_{AB}</math>, <math>E_{BC}</math> oraz <math>E_{CA}</math>, przy czym | |||
: <math>E_{AB}=E_A-E_B</math> | |||
: <math>E_{BC}=E_B-E_C</math> | |||
: <math>E_{CA}=E_C-E_A</math> | |||
Z definicji napięć międzyfazowych wynika, że niezależnie od symetrii ich suma jest zawsze równa zeru gdyż wszystkie napięcia tworzą trójkąt zamknięty. Rysunek na sladzie nr 7 pokazuje układ napięć międzyfazowych generatora trójfazowego z przyjętymi oznaczeniami. Symbol <math>E_{AB}</math> oznacza, że strzałka wektora napięcia na wykresie jest skierowana w stronę pierwszego wskaźnika w oznaczeniu (u nas litera A). | |||
Z symetrii napięć fazowych wynika bezpośrednio symetria napięć międzyfazowych. Napięcia te są równe i przesunięte względem siebie o kąt <math>120^\circ</math>, czyli | |||
: <math>E_{AB}=E_A-E_B</math> | |||
: <math>E_{BC}=E_{AB}e^{-j120^\circ}</math> | |||
: <math>E_{CA}=E_{AB}e^{j120^\circ}</math> | |||
Układ napięć międzyfazowych symetrycznych tworzy więc trójkąt równoboczny. Wykorzystując relacje obowiązujące dla tego trójkąta łatwo jest udowodnić, że napięcie międzyfazowe jest <math>\sqrt{3}</math> razy większe niż napięcie fazowe, co zapiszemy w ogólności jako | |||
: <math>|E_{mf}|=\sqrt{3}|E_f|</math> | |||
gdzie <math>|E_f|</math> oznacza moduł napięcia fazowego a <math>|E_{mf}|</math> moduł napięcia międzyfazowego. | |||
|} | |} | ||
| Linia 77: | Linia 108: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd8.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd8.png]] | ||
|valign="top"| | |valign="top"|'''Analiza układów trójfazowych''' | ||
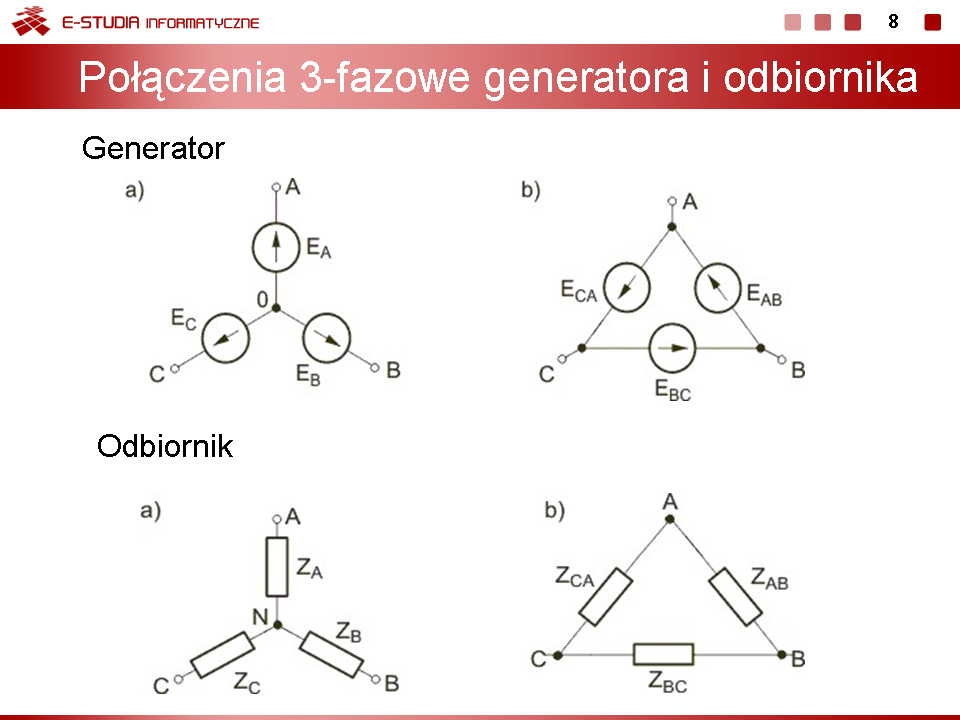
'''Połączenia trójfazowe generatora i odbiornika''' | |||
Układ napięć fazowych generatora może być połączony bądź w gwiazdę bądź w trójkąt. Schemat obu połączeń przedstawiony jest na rysunku obok (slajd nr 8). | |||
Przy połączeniu trójkątnym generatora odbiornik jest zasilany napięciem międzyfazowym trójprzewodowym. Przy połączeniu generatora w gwiazdę napięcie zasilające jest napięciem fazowym a liczba przewodów może być równa trzy bądź cztery (przy czterech przewodach zasilających jednym z nich jest przewód zerowy, zwany również przewodem neutralnym). | |||
|} | |} | ||
| Linia 84: | Linia 121: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd9.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd9.png]] | ||
|valign="top"| | |valign="top"|W układzie trójfazowym odbiornik zawiera również trzy fazy, przy czym może być on połączony w gwiazdę lub w trójkąt. Oba sposoby połączenia odbiornika przedstawione są na rysunku na slajdzie nr 8. | ||
W zależności od sposobu połączenia generatora i odbiornika można w układach trójfazowych wyróżnić cztery rodzaje połączeń. Są to: | |||
*generator i odbiornik połączone w gwiazdę (układ gwiazdowy) | |||
*generator i odbiornik połączone w trójkąt (układ trójkątny) | |||
*generator połączony w gwiazdę a odbiornik w trójkąt | |||
*generator połączony w trójkąt a odbiornik w gwiazdę. | |||
Z punktu widzenia metodyki analizy obwodów istotne są tylko dwa pierwsze rodzaje połączeń. Dwa pozostałe są wtórne względem pierwszych i nie wnoszą nowych elementów do metody analizy. | |||
|} | |} | ||
| Linia 91: | Linia 136: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd10.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd10.png]] | ||
|valign="top"| | |valign="top"|'''Układ gwiazdowy faz generatora i odbiornika''' | ||
Rozpatrzmy układ połączeń gwiazdowych odbiornika i generatora (gwiazda-gwiazda) z oznaczeniami prądów i napięć przedstawionymi na rys. 6.8. | |||
|} | |} | ||
Wersja z 09:46, 1 sie 2006

|
Wykład 6. Układy trójfazowe |

|
Układ gwiazdowy faz generatora i odbiornika
Rozpatrzmy układ połączeń gwiazdowych odbiornika i generatora (gwiazda-gwiazda) z oznaczeniami prądów i napięć przedstawionymi na rys. 6.8. |

|

|

|