Matematyka dyskretna 1/Ćwiczenia 14: Grafy III: Różnice pomiędzy wersjami
m Zastępowanie tekstu - "{\sf" na "\mathsf{" |
m Zastępowanie tekstu - "<div class="thumb t(.*)"><div style="width:(.*)px;"> <flash>file=(.*)\.swf\|width=(.*)\|height=(.*)<\/flash> <div\.thumbcaption>(.*)<\/div><\/div> <\/div>" na "$4x$5px|thumb|$1|$6" |
||
| Linia 15: | Linia 15: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
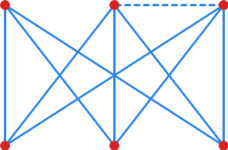
[[File:Cw grafy nieplanarny.svg|300x150px|thumb|right" id="cw_grafy_nieplanarny|1. Graf <math>\displaystyle \mathbf{G} </math>]] | |||
Graf <math>\displaystyle \mathbf{G} </math> przedstawiony na [[#cw grafy nieplanarny|rysunku 1]] nie jest planarny | Graf <math>\displaystyle \mathbf{G} </math> przedstawiony na [[#cw grafy nieplanarny|rysunku 1]] nie jest planarny | ||
Wersja z 15:04, 3 paź 2021
Grafy III
Ćwiczenie 1
Ćwiczenie 2
W pewnym wielościanie wszystkie ściany są pięciokątami i sześciokątami. Ile jest ścian pięciokątnych, jeżeli w każdym wierzchołku spotykają się dokładnie trzy ściany?
Ćwiczenie 3
Pokaż, że dla spójnego, prostego grafu planarnego o co najmniej trzech wierzchołkach zachodzi
Ćwiczenie 4
Pokaż, że spójny graf planarny o co najmniej jednym wierzchołku posiada wierzchołek o stopniu nie większym niż .
Ćwiczenie 5
Znajdź liczbę chromatyczną -wymiarowej kostki , czyli grafu, którego wierzchołki to ciągi , gdzie , a krawędzie łączą te ciągi, które różnią się tylko na jednej pozycji.
Ćwiczenie 6
Nie korzystając z Twierdzenia 14.13 o czterech barwach pokaż, że graf planarny bez trójkątów jest czterokolorowalny.