PEE Moduł 6: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd1.png]] | ||
|valign="top"|'''Wykład 6. Układy trójfazowe''' | |valign="top"|'''Wykład 6. Układy trójfazowe''' | ||
|} | |} | ||
| Linia 7: | Linia 7: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd2.png]] | ||
|valign="top"|'''Pojęcia wstępne''' | |valign="top"|'''Pojęcia wstępne''' | ||
| Linia 18: | Linia 18: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd3.png]] | ||
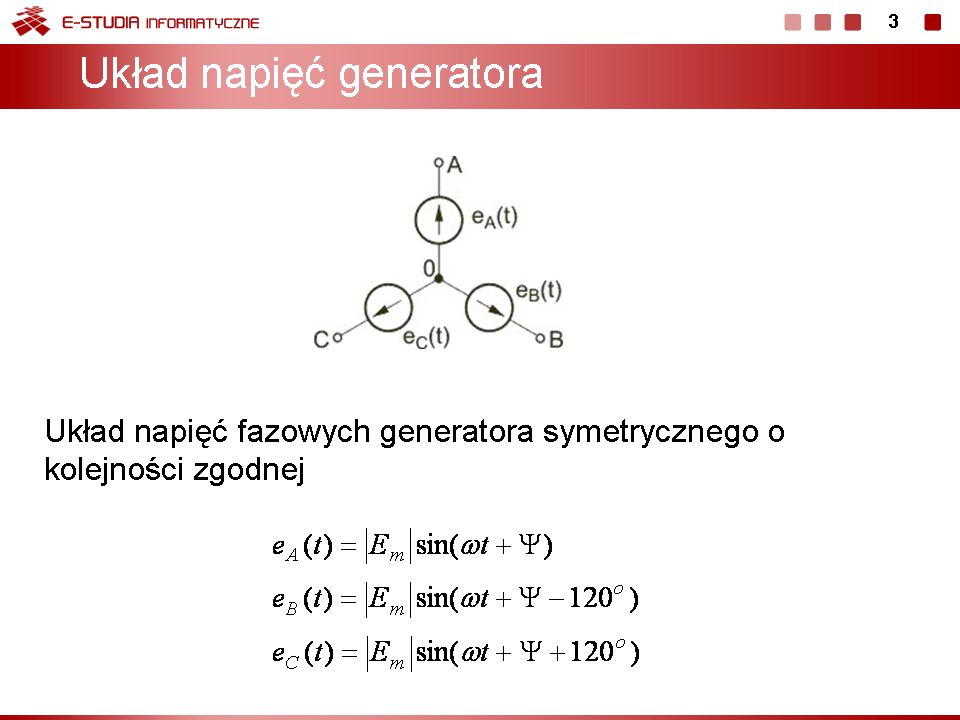
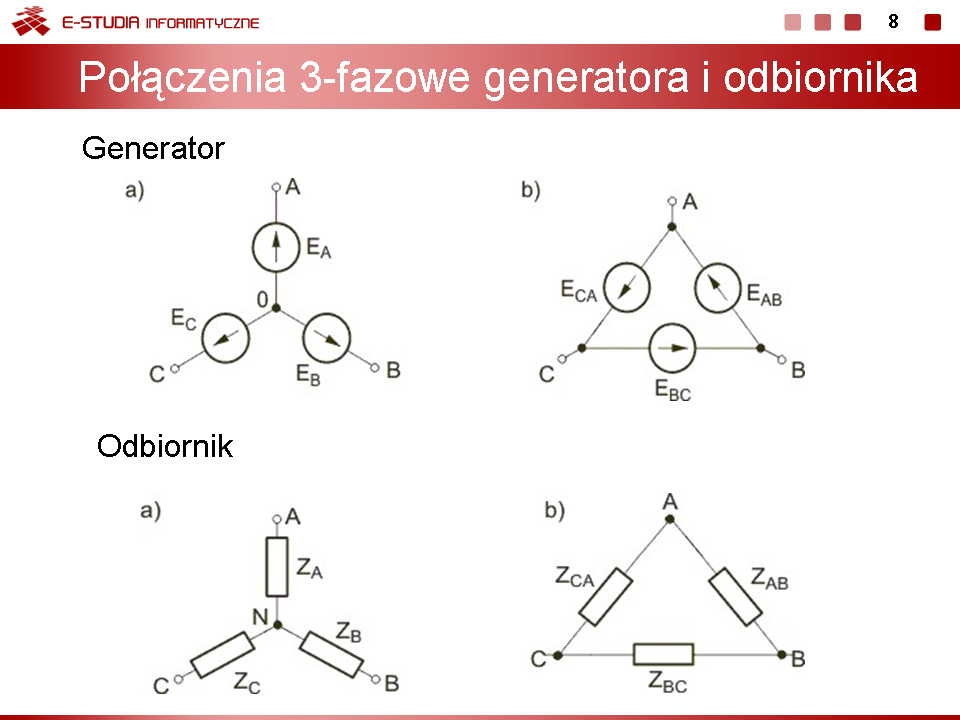
|valign="top"|Przykład połączenia 3 faz generatora w jeden układ gwiazdowy przedstawiony jest na rysunku obok (slajd 3). | |valign="top"|Przykład połączenia 3 faz generatora w jeden układ gwiazdowy przedstawiony jest na rysunku obok (slajd 3). | ||
| Linia 33: | Linia 33: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd4.png]] | ||
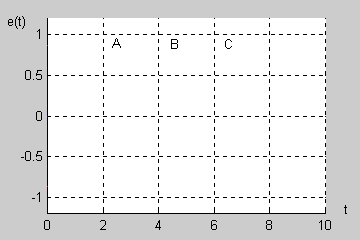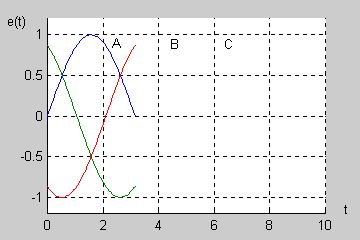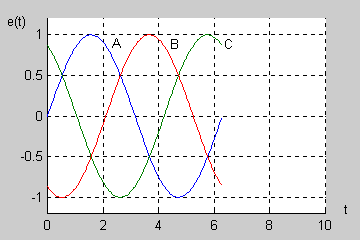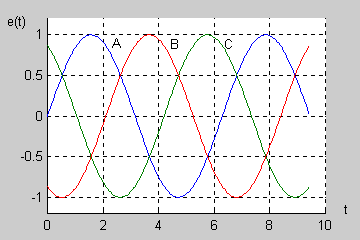
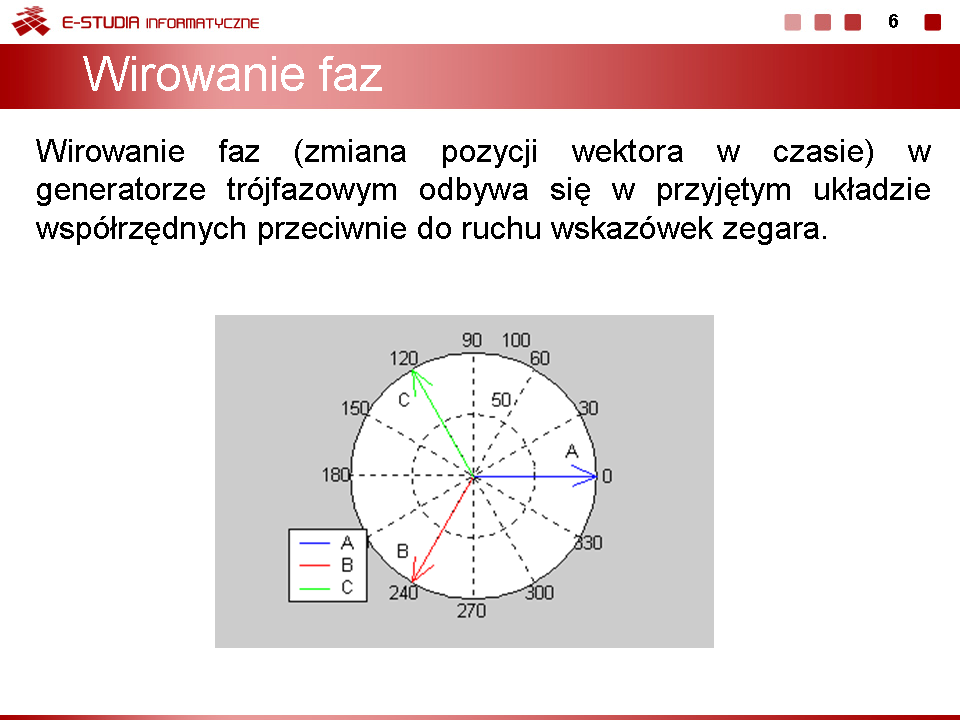
|valign="top"| | |valign="top"|W normalnym systemie trójfazowym przyjmuje się tzw. '''kolejność wirowania zgodną''', w której faza B opóźnia się względem fazy A o kąt <math>120^\circ</math> a faza C (opóźniona względem fazy B o kolejny kąt <math>120^\circ</math> ) wyprzedza fazę A o kąt równy <math>120^\circ</math>. | ||
Na rysunku obok (slajd 4) i poniżej przedstawiono przebiegi czasowe napięć trójfazowych przy kącie początkowym <math>\Psi</math> równym zeru. Napięcia są zmienne sinusoidalnie przy czym występują regularne przesunięcia o kąt <math>120^\circ</math> między poszczególnymi sinusoidami. | |||
[[Grafika:PEE_M6_anim_1.gif]] | |||
|} | |} | ||
| Linia 40: | Linia 45: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd5.png]] | ||
|valign="top"| | |valign="top"|'''Układ napięć fazowych''' | ||
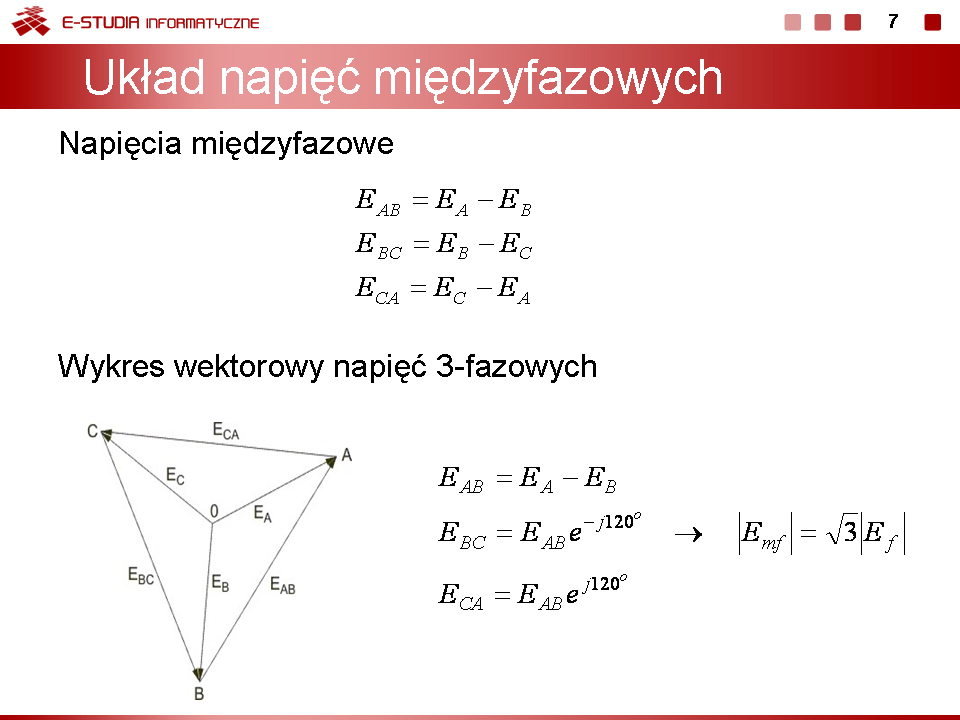
Wobec sinusoidalnej postaci wymuszeń w analizie układów trójfazowych zastosujemy metodę symboliczną. Zgodnie z tą metodą napięcia sinusoidalne zastępuje się ich postacią zespoloną, która dla przyjętych funkcji sinusoidalnych może być zapisana następująco | |||
: <math>E_A={|E_m| \over \sqrt{2}}e^{j\Psi}</math> | |||
: <math>E_B={|E_m| \over \sqrt{2}}e^{j\Psi-120^\circ}=E_Ae^{-j120^\circ}</math> | |||
: <math>E_A={|E_m| \over \sqrt{2}}e^{j\Psi+120^\circ}=E_Ae^{j120^\circ}</math> | |||
W praktyce wobec nieustannej zmiany wartości napięć w czasie faza początkowa <math>\Psi</math> może być przyjęta dowolnie. Najczęściej dla wygody zakładać będziemy, że jest równa zeru. Wykres wektorowy napięć trójfazowych opisanych powyższymi zależnościami dla kąta fazowego <math>\Psi \neq 0</math> przedstawiony jest na rysunku obok (slajd 5). | |||
Punkt wspólny napięć, odpowiadający wspólnemu punktowi połączenia faz generatora oznaczony jest cyfrą 0. Na końcach napięć fazowych zaznaczone są oznaczenia faz (A, B, C). Napięcie fazowe generatora to napięcie między punktem końcowym wektora a punktem zerowym. | |||
|} | |} | ||
| Linia 47: | Linia 62: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd6.png]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
| Linia 54: | Linia 69: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd7.png]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
| Linia 61: | Linia 76: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd8.png]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
| Linia 68: | Linia 83: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd9.png]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
| Linia 75: | Linia 90: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd10.png]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
| Linia 82: | Linia 97: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd11.png]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
| Linia 89: | Linia 104: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd12.png]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
| Linia 96: | Linia 111: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd13.png]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
Wersja z 08:36, 1 sie 2006

|
Wykład 6. Układy trójfazowe |
|
|
|

|

|

|

|

|