PF Moduł 10: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
mNie podano opisu zmian |
||
| Linia 40: | Linia 40: | ||
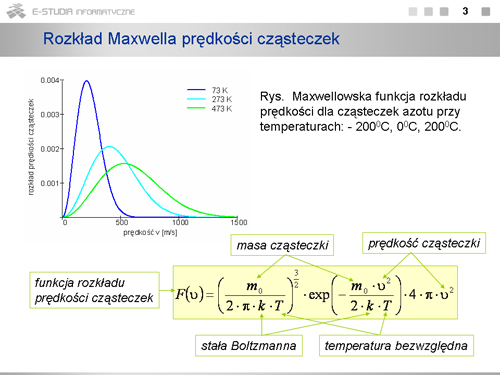
<math>\displaystyle F(v)=\left(\frac{m_0}{2\cdot \pi\cdot k\cdot T} \right)^{3/2}\cdot exp\left(-\frac{m_0\cdot v^2}{2\cdot k\cdot T} \right)\cdot 4\cdot \pi \cdot v^2</math> | <math>\displaystyle F(v)=\left(\frac{m_0}{2\cdot \pi\cdot k\cdot T} \right)^{3/2}\cdot exp\left(-\frac{m_0\cdot v^2}{2\cdot k\cdot T} \right)\cdot 4\cdot \pi \cdot v^2</math> | ||
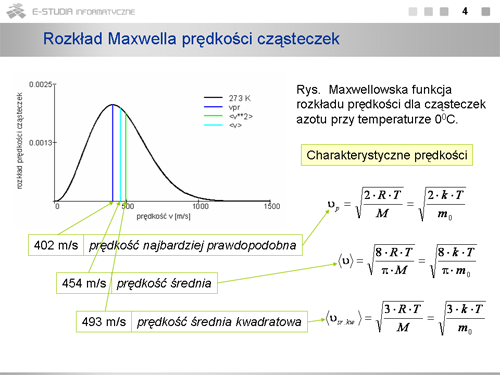
Co jest charakterystyczne w tym rozkładzie <math>F(v)\,</math> ? Jest to konieczność wystąpienia maksimum ze względu na iloczyn rosnącej parabolicznie i malejącej wykładniczo zależności od <math>v\,</math> . (Przeanalizuj dokładnie trzy człony wzoru na <math>F(v)\,</math> . Pierwszy, to czynnik normalizacyjny zawierający wyłącznie wartości stałe, drugi - to człon wykładniczy, ale z ujemną wartością w wykładniku, czyli malejący ze wzrostem prędkości i równy jedynce dla <math>v=0, | Co jest charakterystyczne w tym rozkładzie <math>F(v)\,</math> ? Jest to konieczność wystąpienia maksimum ze względu na iloczyn rosnącej parabolicznie i malejącej wykładniczo zależności od <math>v\,</math> . (Przeanalizuj dokładnie trzy człony wzoru na <math>F(v)\,</math> . Pierwszy, to czynnik normalizacyjny zawierający wyłącznie wartości stałe, drugi - to człon wykładniczy, ale z ujemną wartością w wykładniku, czyli malejący ze wzrostem prędkości i równy jedynce dla <math>v=0,</math> , ostatni - rosnący paraboliczne ze wzrostem prędkości. Rezultat jest zobrazowany na wykresie maxwellowskiej funkcji rozkładu prędkości cząsteczek azotu przy temperaturach: <math>73 K\, (-200^\circ C)\,</math> , <math>273 K\, (0^\circ C)\,</math> , <math>473 K\, (200^\circ C)\,</math>. Gdy temperatura rośnie maksimum krzywej rozkładu przesuwa się w stronę większych prędkości i krzywa ulega spłaszczeniu. Pole pod krzywą równe jest całkowitej liczbie cząsteczek w próbce i pozostaje stałe niezależnie od temperatury. | ||
Rozkład prędkości cząsteczek w danej temperaturze zależy od masy cząsteczek. Im mniejsza masa tym większa liczba cząsteczek o dużych prędkościach. | Rozkład prędkości cząsteczek w danej temperaturze zależy od masy cząsteczek. Im mniejsza masa tym większa liczba cząsteczek o dużych prędkościach. | ||
Wersja z 15:40, 7 paź 2020
Wykład
Materiały do ćwiczeń
Zadanie 10.3
Oblicz zmianę entropii moli gazu doskonałego w procesie izotermicznego rozprężania od objętości do objętości
Rozwiązanie
Zadanie 10.4
Przy jakiej temperaturze średnia prędkość kwadratowa cząsteczek dwutlenku węgla będzie równa średniej prędkości kwadratowej cząsteczek azotu w temperaturze ?
Odpowiedź
Zadanie 10.5
Izolowany układ dwóch zbiorników. Zbiornik o objętości zawierał moli gazu o temperaturze . Zbiornik o objętości zawierał moli również o temperaturze , Oblicz zmianę entropii tych gazów po połączeniu zbiorników i powstaniu mieszaniny.
Odpowiedź
Słowniczek
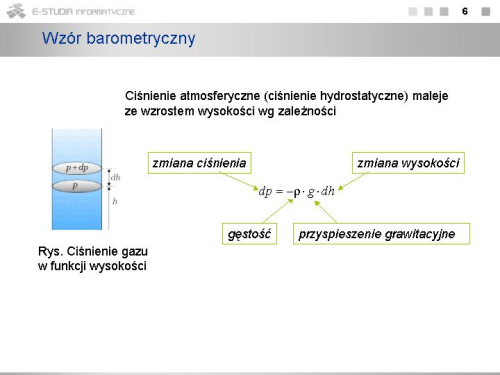
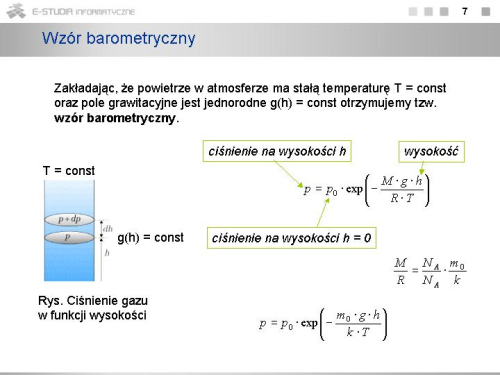
| wzór barometryczny | podaje zależność ciśnienia atmosferycznego od wysokości nad powierzchnią Ziemi |
| rozkład Maxwella prędkości cząsteczek | rozkład wartości prędkości chaotycznego ruchu cząsteczek gazu doskonałego dla zadanej temperatury i masy cząsteczek |
| rozkład Boltzmanna | rozkład koncentracji cząsteczek w funkcji ich wysokości lub energii potencjalnej. Odnosi się nie tylko do pola sił przyciągania ziemskiego, ale do dowolnego pola potencjalnego, jeśli tylko cząsteczki poruszają się chaotycznym ruchem cieplnym. |
| mikrostan | stan układu w którym opisane są stany wszystkich jego elementów |
| hipoteza ergodyczna | Prawdopodobieństwa wszystkich mikrostanów są jednakowe |
| makrostan | stan układu opisany za pomocą wielkości odnoszących się do całości układu |
| prawdopodobieństwo termodynamiczne (waga statystyczna) | odnosi się do makrostanu układu: liczba mikroskoopowych sposobów realizacji danego makrostanu (liczba mikrostanów odpowiadająca danemu makrostanowi) |
| entropia | definicja statystyczna: wielkość proporcjonalna do logarytmu prawdopodobieństwa termodynamicznego stanu układu |
| fluktuacje | losowe odchylenia danej wielkości od wartości średniej |
| prawo wzrostu entropii | entropia układu izolowanego nie może maleć, w procesach nieodwracalnych entropia układu rośnie |