GKIW Moduł 4: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 19: | Linia 19: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_1.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_1.png|thumb|500px]] | ||
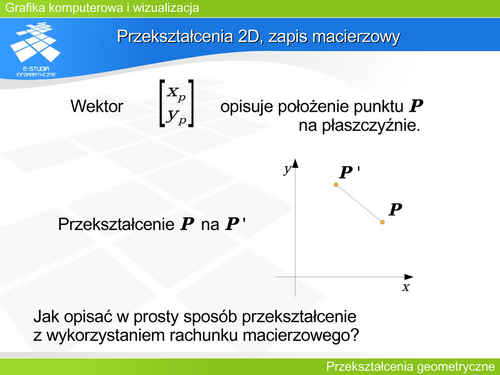
|valign="top"| | |valign="top"|Współczesna grafika komputerowa operuje na milionach elementów (punktów, trójkątów). Przy tak dużej liczbie zachodzi konieczność opisania operacji geometrycznych w taki sposób, aby ich wykonanie było z jednej strony efektywne, a z drugiej, aby opis był prosty i ujednolicony. Takie warunki spełnia opis macierzowy. | ||
Współczesna grafika komputerowa operuje na milionach elementów (punktów, trójkątów). Przy tak dużej liczbie zachodzi konieczność opisania operacji geometrycznych w taki sposób, aby ich wykonanie było z jednej strony efektywne, a z drugiej, aby opis był prosty i ujednolicony. Takie warunki spełnia opis macierzowy. | |||
Niech <math>P=\begin{bmatrix} x_p & y_p \\ \end{bmatrix}^T</math> opisuje położenie punktu na płaszczyźnie. Najprostszym rozwiązaniem byłoby przyjęcie, że macierz <math>M(2\times 2)</math> opisuje przekształcenie punktu <math>P\,</math> na <math>P'\,</math> i że <math>P'=M\cdot P</math> | Niech <math>P=\begin{bmatrix} x_p & y_p \\ \end{bmatrix}^T</math> opisuje położenie punktu na płaszczyźnie. Najprostszym rozwiązaniem byłoby przyjęcie, że macierz <math>M(2\times 2)</math> opisuje przekształcenie punktu <math>P\,</math> na <math>P'\,</math> i że <math>P'=M\cdot P</math> | ||
| Linia 30: | Linia 28: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_2.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_2.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Można zastanowić się nad tym, czy takie podejście do problemu wystarczy do opisu prostych operacji geometrycznych. | ||
Można zastanowić się nad tym, czy takie podejście do problemu wystarczy do opisu prostych operacji geometrycznych. | |||
Rozpatrzmy zestaw przekształceń na płaszczyźnie: obrót, skalowanie, przesunięcie (translację). | Rozpatrzmy zestaw przekształceń na płaszczyźnie: obrót, skalowanie, przesunięcie (translację). | ||
| Linia 45: | Linia 41: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_3.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_3.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Niech <math>M_{T1}=\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}</math>. Niech wektor <math>P=\begin{bmatrix} T_X & T_Y \\ \end{bmatrix}</math> opisuje translację punktu na płaszczyźnie. | ||
Niech <math>M_{T1}=\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}</math>. Niech wektor <math>P=\begin{bmatrix} T_X & T_Y \\ \end{bmatrix}</math> opisuje translację punktu na płaszczyźnie. | |||
Czy można znaleźć takie a, b, c, d, aby <math>M_{T1}=\begin{bmatrix} x_p+T_X \\ y_p+T_Y \\ \end{bmatrix}=\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}\cdot \begin{bmatrix} x_p \\ y_p \\ \end{bmatrix}</math> dla <math>T_X\neq 0</math> i <math>T_Y\neq 0</math> . | Czy można znaleźć takie a, b, c, d, aby <math>M_{T1}=\begin{bmatrix} x_p+T_X \\ y_p+T_Y \\ \end{bmatrix}=\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}\cdot \begin{bmatrix} x_p \\ y_p \\ \end{bmatrix}</math> dla <math>T_X\neq 0</math> i <math>T_Y\neq 0</math> . | ||
| Linia 73: | Linia 67: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_4.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_4.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Niech <math>x_p, y_p, z_p\,</math>, opisują położenie punktu w trójwymiarowym kartezjańskim układzie współrzędnych. W grafice komputerowej do opisu położenia oraz opisu operacji (transformacji geometrycznych), którym punkty będą podlegały, jest używany '''układ współrzędnych jednorodnych znormalizowanych'''. Dzięki temu wszystkie stosowane transformacje geometryczne mogą być opisane w identyczny sposób za pomocą mnożenia macierzowego. Jeśli współrzędne <math>x_p, y_p, z_p\,</math> opisują położenie punktu, to odpowiada temu wektor <math>P=\begin{bmatrix} x_p & y_p & z_p & 1 \\ \end{bmatrix}^T</math> we współrzędnych jednorodnych znormalizowanych. We współrzędnych nieznormalizowanych wektor ten miałby postać <math>P=\begin{bmatrix} \overset{\sim}{x_p} & \overset{\sim}{y_p} & \overset{\sim}{z_p} & \overset{\sim}{N} \\ \end{bmatrix}^T</math> dla <math>\overset{\sim}{N}\neq 0</math> . Przy czym <math>\displaystyle x_p=\frac{\overset{\sim}{x_p}}{\overset{\sim}{N}}</math> , <math>\displaystyle y_p=\frac{\overset{\sim}{y_p}}{\overset{\sim}{N}}</math> , <math>\displaystyle z_p=\frac{\overset{\sim}{z_p}}{\overset{\sim}{N}}</math> , co nosi nazwę operacji normalizacji. | ||
Niech <math>x_p, y_p, z_p\,</math>, opisują położenie punktu w trójwymiarowym kartezjańskim układzie współrzędnych. W grafice komputerowej do opisu położenia oraz opisu operacji (transformacji geometrycznych), którym punkty będą podlegały, jest używany '''układ współrzędnych jednorodnych znormalizowanych'''. Dzięki temu wszystkie stosowane transformacje geometryczne mogą być opisane w identyczny sposób za pomocą mnożenia macierzowego. Jeśli współrzędne <math>x_p, y_p, z_p\,</math> opisują położenie punktu, to odpowiada temu wektor <math>P=\begin{bmatrix} x_p & y_p & z_p & 1 \\ \end{bmatrix}^T</math> we współrzędnych jednorodnych znormalizowanych. We współrzędnych nieznormalizowanych wektor ten miałby postać <math>P=\begin{bmatrix} \overset{\sim}{x_p} & \overset{\sim}{y_p} & \overset{\sim}{z_p} & \overset{\sim}{N} \\ \end{bmatrix}^T</math> dla <math>\overset{\sim}{N}\neq 0</math> . Przy czym <math>\displaystyle x_p=\frac{\overset{\sim}{x_p}}{\overset{\sim}{N}}</math> , <math>\displaystyle y_p=\frac{\overset{\sim}{y_p}}{\overset{\sim}{N}}</math> , <math>\displaystyle z_p=\frac{\overset{\sim}{z_p}}{\overset{\sim}{N}}</math> , co nosi nazwę operacji normalizacji. | |||
Zastosowanie w przypadku przesunięcia na płaszczyźnie współrzędnych jednorodnych można sobie wyobrazić jako umieszczenie płaszczyzny, na której pracujemy, w trójwymiarowym układzie współrzędnych, w taki sposób, aby nie przechodziła ona przez początek układu (tzn. dla <math>z=h_z\neq 0</math> ). Wtedy analogiczne opisanie operacji translacji na płaszczyźnie (ale już jako macierz 3x3) da poprawne rozwiązanie, gdyż punkt stały – początek układu współrzędnych jest poza płaszczyzną, na której jest wykonywana operacja. Jednocześnie, aby wynik operacji znajdował się na tej samej płaszczyźnie, najprościej operować na współrzędnych znormalizowanych, czyli pracować na płaszczyźnie <math>z=1</math>. | Zastosowanie w przypadku przesunięcia na płaszczyźnie współrzędnych jednorodnych można sobie wyobrazić jako umieszczenie płaszczyzny, na której pracujemy, w trójwymiarowym układzie współrzędnych, w taki sposób, aby nie przechodziła ona przez początek układu (tzn. dla <math>z=h_z\neq 0</math> ). Wtedy analogiczne opisanie operacji translacji na płaszczyźnie (ale już jako macierz 3x3) da poprawne rozwiązanie, gdyż punkt stały – początek układu współrzędnych jest poza płaszczyzną, na której jest wykonywana operacja. Jednocześnie, aby wynik operacji znajdował się na tej samej płaszczyźnie, najprościej operować na współrzędnych znormalizowanych, czyli pracować na płaszczyźnie <math>z=1</math>. | ||
| Linia 91: | Linia 83: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_5.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_5.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Niech położenie punktu o współrzędnych <math>(x_p, y_p)</math> na płaszczyźnie reprezentuje wektor P : | ||
Niech położenie punktu o współrzędnych <math>(x_p, y_p)</math> na płaszczyźnie reprezentuje wektor P : | |||
:<math>P=\begin{bmatrix} x_P \\y_P \\ 1 \end{bmatrix}</math> | :<math>P=\begin{bmatrix} x_P \\y_P \\ 1 \end{bmatrix}</math> | ||
| Linia 127: | Linia 117: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_6.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_6.png|thumb|500px]] | ||
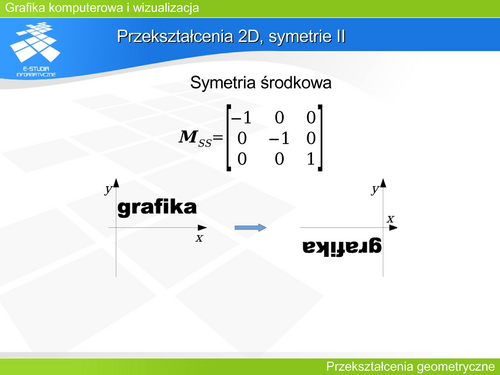
|valign="top"| | |valign="top"|Można zaproponować pewien minimalny zestaw operacji: symetrie (względem osi układu współrzędnych i środkowa), obroty, przesunięcie (translacja), skalowanie oraz pochylenie. | ||
Można zaproponować pewien minimalny zestaw operacji: symetrie (względem osi układu współrzędnych i środkowa), obroty, przesunięcie (translacja), skalowanie oraz pochylenie. | |||
|} | |} | ||
| Linia 165: | Linia 153: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_11.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_11.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Pochylenie jest rzadziej stosowanym przekształceniem. Daje możliwość zniekształcenia figury. Nie zachowuje odległości punktów. Figura i jej obraz w tym przekształceniu nie są podobne. | ||
Pochylenie jest rzadziej stosowanym przekształceniem. Daje możliwość zniekształcenia figury. Nie zachowuje odległości punktów. Figura i jej obraz w tym przekształceniu nie są podobne. | |||
|} | |} | ||
| Linia 175: | Linia 161: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_12.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_12.png|thumb|500px]] | ||
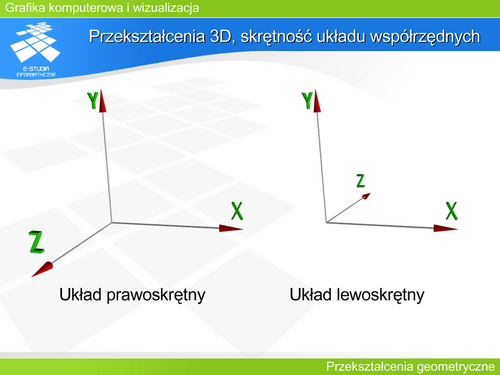
|valign="top"| | |valign="top"|Możliwe są dwa ustawienia osi trójwymiarowego układu współrzędnych. Najczęściej do opisu położenia obiektów na scenie (w przestrzeni obiektu) stosowany jest układ prawoskrętny. Natomiast w operacjach związanych z rzutowaniem układ lewoskrętny. Wybór układu współrzędnych dla operacji rzutowania jest konsekwencją naturalnego rozumienia odległości obiektu od obserwatora. Jeśli osie OX i OY zdefiniują układ współrzędnych na rzutni (utożsamianej z płaszczyzną XOY) (pozioma oś OX skierowana w prawo i pionowa oś OY skierowana do góry), to kierunek wzrostu odległości od obserwatora wskaże oś OZ. Tak zdefiniowany układ współrzędnych będzie układem lewoskrętnym. | ||
Możliwe są dwa ustawienia osi trójwymiarowego układu współrzędnych. Najczęściej do opisu położenia obiektów na scenie (w przestrzeni obiektu) stosowany jest układ prawoskrętny. Natomiast w operacjach związanych z rzutowaniem układ lewoskrętny. Wybór układu współrzędnych dla operacji rzutowania jest konsekwencją naturalnego rozumienia odległości obiektu od obserwatora. Jeśli osie OX i OY zdefiniują układ współrzędnych na rzutni (utożsamianej z płaszczyzną XOY) (pozioma oś OX skierowana w prawo i pionowa oś OY skierowana do góry), to kierunek wzrostu odległości od obserwatora wskaże oś OZ. Tak zdefiniowany układ współrzędnych będzie układem lewoskrętnym. | |||
Niech położenie punktu o współrzędnych <math>(x_p, y_p, z_p)</math> w przestrzeni trójwymiarowej reprezentuje wektor P : | Niech położenie punktu o współrzędnych <math>(x_p, y_p, z_p)</math> w przestrzeni trójwymiarowej reprezentuje wektor P : | ||
| Linia 208: | Linia 192: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_14.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_14.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Macierze opisujące symetrie płaszczyznowe względem pozostałych dwóch płaszczyzn (XOY i YOZ) mają analogiczną postać ze zmienionym znakiem przy 1 w odpowiedniej kolumnie. | ||
Macierze opisujące symetrie płaszczyznowe względem pozostałych dwóch płaszczyzn (XOY i YOZ) mają analogiczną postać ze zmienionym znakiem przy 1 w odpowiedniej kolumnie. | |||
|} | |} | ||
| Linia 217: | Linia 199: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_15.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_15.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Podobnie macierze opisujące symetrie osiowe względem pozostałych dwóch osi (OY i OZ) mają analogiczną postać ze zmienionymi znakami. | ||
Podobnie macierze opisujące symetrie osiowe względem pozostałych dwóch osi (OY i OZ) mają analogiczną postać ze zmienionymi znakami. | |||
|} | |} | ||
| Linia 233: | Linia 213: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_17.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_17.png|thumb|500px]] | ||
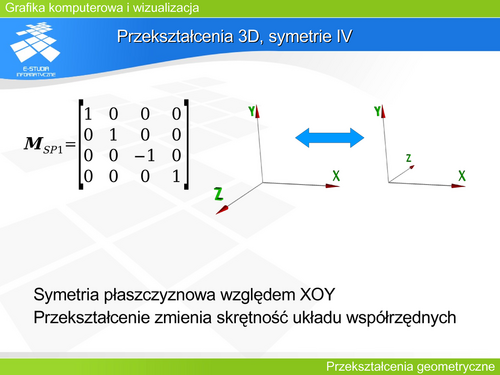
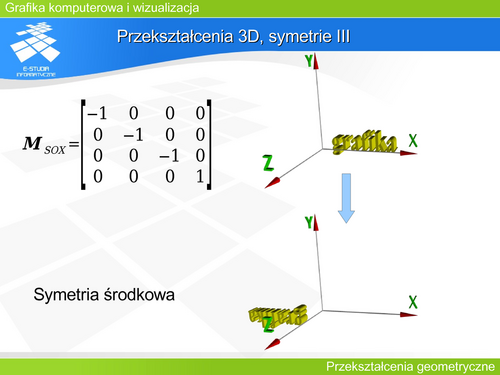
|valign="top"| | |valign="top"|Jeżeli założyliśmy, że położenie obiektów sceny będzie opisywane w układzie prawoskrętnym, natomiast rzutowanie będzie rozpatrywane w układzie lewoskrętnym, to współrzędne tego samego punktu w obu układach będą się różniły znakiem przy współrzędnej z. Przeliczenie współrzędnych między układami zapewnia macierz symetrii płaszczyznowej względem XOY. | ||
Jeżeli założyliśmy, że położenie obiektów sceny będzie opisywane w układzie prawoskrętnym, natomiast rzutowanie będzie rozpatrywane w układzie lewoskrętnym, to współrzędne tego samego punktu w obu układach będą się różniły znakiem przy współrzędnej z. Przeliczenie współrzędnych między układami zapewnia macierz symetrii płaszczyznowej względem XOY. | |||
|} | |} | ||
| Linia 242: | Linia 220: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_18.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M4_Slajd_18.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Przesunięcie w układzie trójwymiarowym odbywa się w sposób analogiczny do przesunięcia na płaszczyźnie. | ||
Przesunięcie w układzie trójwymiarowym odbywa się w sposób analogiczny do przesunięcia na płaszczyźnie. | |||
|} | |} | ||
Wersja z 12:16, 5 lut 2007
Wykład
 |
 |
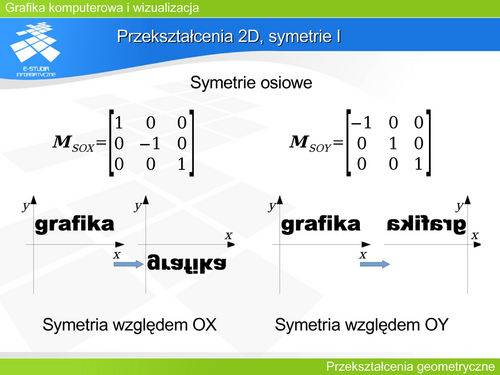 |
Można zaproponować pewien minimalny zestaw operacji: symetrie (względem osi układu współrzędnych i środkowa), obroty, przesunięcie (translacja), skalowanie oraz pochylenie. |
 |
 |
 |
 |
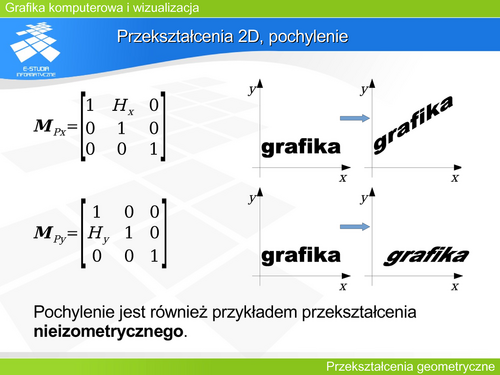 |
Pochylenie jest rzadziej stosowanym przekształceniem. Daje możliwość zniekształcenia figury. Nie zachowuje odległości punktów. Figura i jej obraz w tym przekształceniu nie są podobne. |
 |
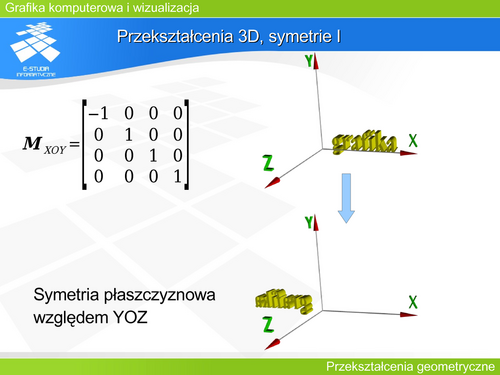 |
Macierze opisujące symetrie płaszczyznowe względem pozostałych dwóch płaszczyzn (XOY i YOZ) mają analogiczną postać ze zmienionym znakiem przy 1 w odpowiedniej kolumnie. |
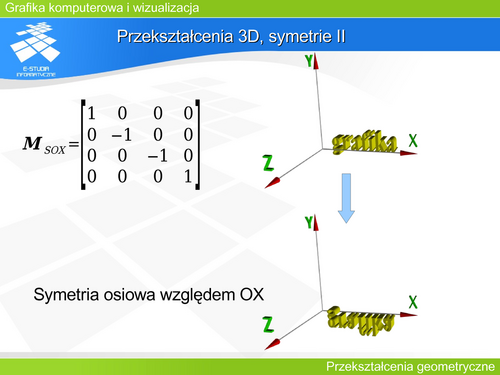 |
Podobnie macierze opisujące symetrie osiowe względem pozostałych dwóch osi (OY i OZ) mają analogiczną postać ze zmienionymi znakami. |
 |
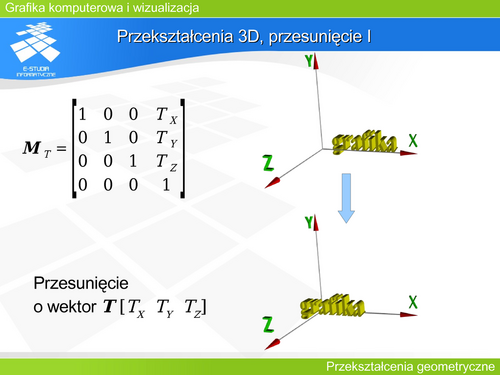 |
Przesunięcie w układzie trójwymiarowym odbywa się w sposób analogiczny do przesunięcia na płaszczyźnie. |
 |
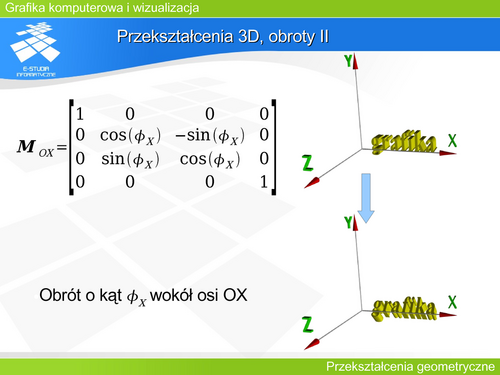 |
Przekształcenie 3D, obroty II
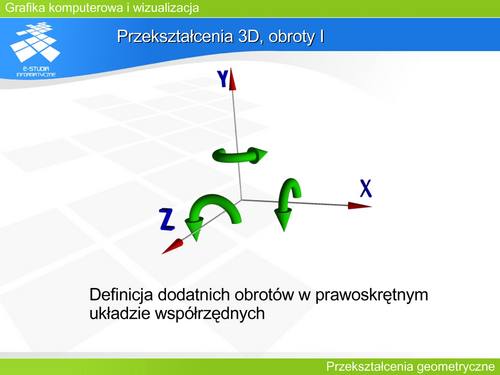
Obiekt na rysunku został obrócony o kat wokół osi OX. |
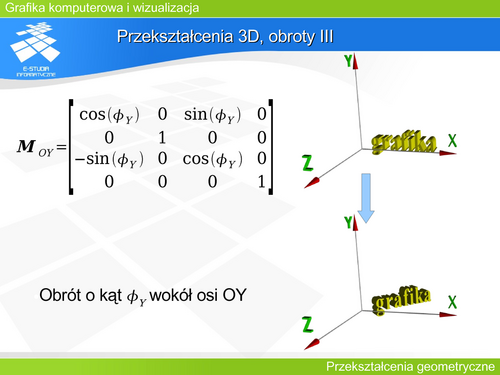 |
Przekształcenie 3D, obroty III
Obiekt na rysunku został obrócony o kat wokół osi OY |
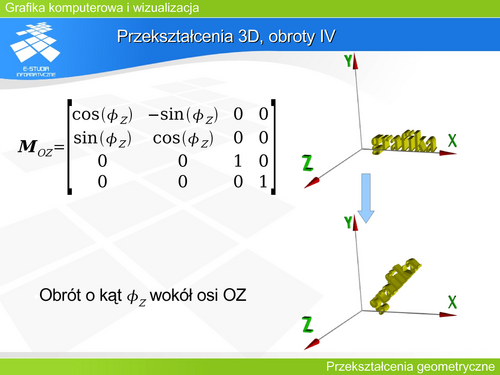 |
Przekształcenie 3D, obroty IV
Obiekt na rysunku został obrócony o kat wokół osi OZ. |
 |
Przykład obrotu wokół prostej l III
Po zrealizowaniu obrotu wokół OX prosta l znalazła się na płaszczyźnie XOZ. |
 |
Przykład obrotu wokół prostej l IV
Po zrealizowaniu obrotu wokół OY prosta l pokryje się z osią OX układu współrzędnych. Jednocześnie odpowiednio dobrane operacje zapewniły zgodność zwrotów obu osi. |
 |
Przykład obrotu wokół prostej l V
Teraz można wreszcie wykonać obrót o kąt wokół prostej l co, dzięki odpowiednim operacjom wstępnym, odpowiada obrotowi o kąt wokół osi OX układu współrzędnych. |
 |
Kwaterniony II
Suma i iloczyn są zdefiniowane tak jak na rysunku. Dodawanie kwaternionów jest operacją łączną i przemienną. Mnożenie kwaternionów jest operacją łączną i nie jest operacją przemienną |
 |