PEE Moduł 11: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 265: | Linia 265: | ||
|valign="top"|W tym przypadku można napisać: | |valign="top"|W tym przypadku można napisać: | ||
<math>P_p = P_a +p </math> | <math>P_p = P_a +p </math> | ||
<math>N_p = n </math> | |||
<math>N_p = n </math> | |||
gdzie | gdzie | ||
*<math>P_p</math> – koncentracja dziur w półprzewodniku typu p | *<math>P_p</math> – koncentracja dziur w półprzewodniku typu p | ||
*<math>p\,</math> – koncentracja dziur na skutek generacji termicznej | *<math>p\,</math> – koncentracja dziur na skutek generacji termicznej | ||
| Linia 290: | Linia 293: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd22.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M11_Slajd22.png|thumb|500px]] | ||
|valign="top"|Obszar, w którym zachodzi bardzo silna (o kilka rzędów wielkości) zmiana koncentracji ładunku | |valign="top"|Obszar, w którym zachodzi bardzo silna (o kilka rzędów wielkości) zmiana koncentracji ładunku nazywa się złączem. | ||
Szerokość złącza ma na ogół wymiar rzędu <math>10^{-7}-10^{-6} m</math>. | Szerokość złącza ma na ogół wymiar rzędu <math>10^{-7}-10^{-6} m</math>. | ||
| Linia 321: | Linia 325: | ||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd25.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M11_Slajd25.png|thumb|500px]] | ||
|valign="top"|Proces rekombinacji jest opóźniony względem procesu generacji o krótki rzędu mikrosekund czas τ nazywany czasem życia nośników. Wartość tego czasu mówi o jakości struktury krystalicznej półprzewodnika oraz o stopniu jej uporządkowania. Obróbka termiczna w wysokich temperaturach skraca o rząd wielkości czas życia nośników. W czasie τ nośniki ładunku przebywają pewien odcinek drogi L nazywany drogą dyfuzji. Droga dyfuzji jest związana z czasem życia nośników równaniem: | |valign="top"|Proces rekombinacji jest opóźniony względem procesu generacji o krótki rzędu mikrosekund czas τ nazywany czasem życia nośników. Wartość tego czasu mówi o jakości struktury krystalicznej półprzewodnika oraz o stopniu jej uporządkowania. Obróbka termiczna w wysokich temperaturach skraca o rząd wielkości czas życia nośników. W czasie τ nośniki ładunku przebywają pewien odcinek drogi L nazywany drogą dyfuzji. Droga dyfuzji jest związana z czasem życia nośników równaniem: | ||
<math>L=\sqrt D\tau</math> | <math>L=\sqrt D\tau</math> | ||
gdzie D – stała dyfuzji | gdzie D – stała dyfuzji | ||
W temperaturze pokojowej 300 K <math>D_n = 35\cdot 10^{-4} m^2s^{-1}</math>, <math>D_p = 12,5\cdot 10^{-4} m^2s^{-1}</math> | |||
|} | |} | ||
| Linia 346: | Linia 351: | ||
<math>i=\frac{dQ}{dt}</math> | <math>\displaystyle i=\frac{dQ}{dt}</math> | ||
| Linia 364: | Linia 369: | ||
<math>\gamma =e(n\frac{v_x_n}{E_x}+\frac{v_x_p}{E_x})</math> | <math>\displaystyle \gamma =e(n\frac{v_x_n}{E_x}+\frac{v_x_p}{E_x})</math> | ||
Parametry <math>\frac{v_x_n}{E_x}\mu_n</math> oraz <math>\frac{v_x_n}{E_x}\mu_n</math> nazywamy ruchliwością nośników, odpowiednio elektronów i dziur. Ich wartość leży w zakresie <math>10^-^3 \div 10^-^2 m^2/ | Parametry <math>\displaystyle \frac{v_x_n}{E_x}\mu_n</math> oraz <math>\displaystyle \frac{v_x_n}{E_x}\mu_n</math> nazywamy ruchliwością nośników, odpowiednio elektronów i dziur. Ich wartość leży w zakresie <math>10^-^3 \div 10^-^2 m^2/V\cdot s</math> dla metali, | ||
<math>4\cdot10^-^2 \div 4\cdot 10^-^1 m^2/V\ | <math>4\cdot10^-^2 \div 4\cdot 10^-^1 m^2/V\cdot s</math> dla krzemu i germanu oraz około <math>7 m^2/V\cdot s</math> dla innych półprzewodników typu III – V i zmienia się w funkcji temperatury. Dla krzemu obowiązuje zależność <math>µ_n = 3µ_p</math>. | ||
| Linia 402: | Linia 407: | ||
|valign="top"|W stanie równowagi termicznej suma prądu unoszenia i dyfuzji jest równa zeru. Dokładniejsze badanie warunków równowagi pozwala wyznaczyć tzw. zależność Einsteina wiążącą ruchliwość ładunku ze współczynnikiem dyfuzji: | |valign="top"|W stanie równowagi termicznej suma prądu unoszenia i dyfuzji jest równa zeru. Dokładniejsze badanie warunków równowagi pozwala wyznaczyć tzw. zależność Einsteina wiążącą ruchliwość ładunku ze współczynnikiem dyfuzji: | ||
<math>\frac{D_n}{\mu_n}=\frac{D_p}{\mu_p}=\frac{kT}{e}=U_T</math> | <math>\displaystyle \frac{D_n}{\mu_n}=\frac{D_p}{\mu_p}=\frac{kT}{e}=U_T</math> | ||
gdzie UT potencjał elektrokinetyczny. | gdzie UT potencjał elektrokinetyczny. | ||
| Linia 416: | Linia 421: | ||
<math>J_n(X)=J_u_n+J_d_n=e\mu_n n(X)E_x+eD_n\frac{dn(X)}{dx}</math> | <math>\displaystyle J_n(X)=J_u_n+J_d_n=e\mu_n n(X)E_x+eD_n\frac{dn(X)}{dx}</math> | ||
<math>J_p(X)=J_u_p+J_d_p=e\mu_p p(X)E_x+eD_n\frac{dp(X)}{dx}</math> | <math>\displaystyle J_p(X)=J_u_p+J_d_p=e\mu_p p(X)E_x+eD_n\frac{dp(X)}{dx}</math> | ||
|} | |} | ||
| Linia 429: | Linia 434: | ||
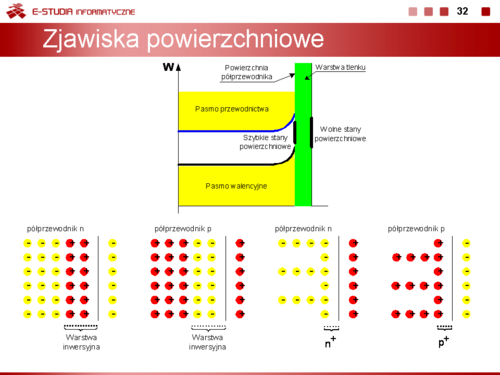
|valign="top"|'''Zjawiska powierzchniowe''' | |valign="top"|'''Zjawiska powierzchniowe''' | ||
Na powierzchni półprzewodnika występuje w sposób naturalny nieciągłość sieci krystalicznej. W modelu pasmowym oznacza to, że pojawiają się na granicy materiału tzw. energetyczne stany powierzchniowe, które mogą być obsadzone przez elektrony. Stany te są | Na powierzchni półprzewodnika występuje w sposób naturalny nieciągłość sieci krystalicznej. W modelu pasmowym oznacza to, że pojawiają się na granicy materiału tzw. energetyczne stany powierzchniowe, które mogą być obsadzone przez elektrony. Stany te są usytuowane w pobliżu środka pasma zabronionego. Wyróżnia się tzw. stany szybkie, powstające na powierzchni czystego półprzewodnika i stany wolne, w przypadku, gdy powierzchnia półprzewodnika pokryta jest warstwą tlenku. Stany powierzchniowe mogą być donorowe lub akceptorowe. Powodują one, że na powierzchni półprzewodnika w cienkiej warstwie o grubości od kilku do kilkudziesięciu angstremów <math>(1 \overset{\circ}{A} = 10^-^{10} m)</math> gromadzi się ładunek ujemny (elektrony) lub dodatni (dziury). W wyniku oddziaływania tej warstwy na ładunki znajdujące się wewnątrz półprzewodnika w pobliżu jego powierzchni powstaje tzw. warstwa inwersyjna ładunku przeciwnego znaku | ||
| Linia 440: | Linia 445: | ||
<math>L_D\sqrt \frac{2\epsilon \cdot \epsilon_0 \cdot k\cdot T}{n\cdot e^2}</math> | <math>\displaystyle L_D=\sqrt \frac{2\epsilon \cdot \epsilon_0 \cdot k\cdot T}{n\cdot e^2}</math> | ||
gdzie | gdzie | ||
| Linia 471: | Linia 476: | ||
<math>U_s_z=\sqrt {kTR\Delta f}</math> | <math>\displaystyle U_s_z=\sqrt {kTR\Delta f}</math> | ||
gdzie R – rezystancja próbki materiału | gdzie R – rezystancja próbki materiału | ||
| Linia 483: | Linia 488: | ||
|valign="top"|Szumy śrutowe spowodowane są występowaniem statystycznych fluktuacji procesów związanych z generacją, rekombinacją i dyfuzją nośników ładunków w półprzewodniku podczas przepływu prądu. Wartość skuteczna zastępczego źródła prądu reprezentującego te szumy w zakresie częstotliwości <math>\Delta f</math> jest równa: | |valign="top"|Szumy śrutowe spowodowane są występowaniem statystycznych fluktuacji procesów związanych z generacją, rekombinacją i dyfuzją nośników ładunków w półprzewodniku podczas przepływu prądu. Wartość skuteczna zastępczego źródła prądu reprezentującego te szumy w zakresie częstotliwości <math>\Delta f</math> jest równa: | ||
<math>I_s_z=\sqrt{ 2e\Delta fi_0}</math> | <math>\displaystyle I_s_z=\sqrt{ 2e\Delta fi_0}</math> | ||
gdzie <math>I_0</math> – składowa stała przepływającego przez próbkę prądu. | gdzie <math>I_0</math> – składowa stała przepływającego przez próbkę prądu. | ||
| Linia 495: | Linia 500: | ||
|valign="top"|Szumy strukturalne, czasami nazywane modulacyjnymi, wywołane są zjawiskami powierzchniowymi. Wartość skuteczna zastępczego źródła prądu reprezentującego te szumy w zakresie częstotliwości <math>\Delta f</math> maleje ze wzrostem częstotliwości i jest równa: | |valign="top"|Szumy strukturalne, czasami nazywane modulacyjnymi, wywołane są zjawiskami powierzchniowymi. Wartość skuteczna zastępczego źródła prądu reprezentującego te szumy w zakresie częstotliwości <math>\Delta f</math> maleje ze wzrostem częstotliwości i jest równa: | ||
<math>I_s_z= | <math>\displaystyle I_s_z=AI_0\frac{\Delta f}{f}</math> | ||
gdzie A – stała zależna od wymiarów i parametrów materiału półprzewodnikowego. | gdzie A – stała zależna od wymiarów i parametrów materiału półprzewodnikowego. | ||
| Linia 508: | Linia 513: | ||
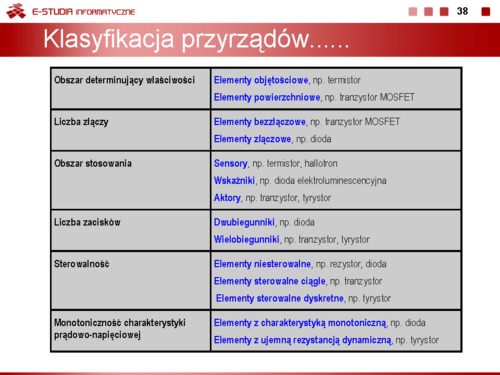
Przyrządy półprzewodnikowe klasyfikujemy przyjmując różne kryteria podziału. Przyjmując jako kryterium liczbę złącz półprzewodnikowych dzielimy przyrządy półprzewodnikowe na bezzłączowe, jednozłączowe i wielozłączowe, a ze względu na liczbę wyprowadzeń na dwu-, trój- i wielozaciskowe. | Przyrządy półprzewodnikowe klasyfikujemy przyjmując różne kryteria podziału. Przyjmując jako kryterium liczbę złącz półprzewodnikowych dzielimy przyrządy półprzewodnikowe na bezzłączowe, jednozłączowe i wielozłączowe, a ze względu na liczbę wyprowadzeń na dwu-, trój- i wielozaciskowe. | ||
Ze względu na obszar, w którym zachodzą zjawiska fizyczne decydujące | Ze względu na obszar, w którym zachodzą zjawiska fizyczne decydujące | ||
o właściwościach elektrycznych dzielimy przyrządy półprzewodnikowe na takie, w których występują efekty objętościowe (decydują zjawiska zachodzące w całej objętości materiału półprzewodnikowego) i takie, w których występują efekty powierzchniowe (decydują zjawiska zachodzące na powierzchni materiału półprzewodnikowego). | o właściwościach elektrycznych dzielimy przyrządy półprzewodnikowe na takie, w których występują efekty objętościowe (decydują zjawiska zachodzące w całej objętości materiału półprzewodnikowego) i takie, w których występują efekty powierzchniowe (decydują zjawiska zachodzące na powierzchni materiału półprzewodnikowego). | ||
Przyjmując jako kryterium możliwość wzmacniania sygnałów dzielimy przyrządy półprzewodnikowe na pasywne (tłumią sygnały) i aktywne (umożliwiają wzmacnianie sygnałów). | Przyjmując jako kryterium możliwość wzmacniania sygnałów dzielimy przyrządy półprzewodnikowe na pasywne (tłumią sygnały) i aktywne (umożliwiają wzmacnianie sygnałów). | ||
Ze względu na możliwość zmiany stanu pracy elementu dzielimy przyrządy półprzewodnikowe na sterowalne i niesterowalne, a z punktu widzenia energetycznego na przyrządy małej mocy (sygnałowe) i przyrządy mocy (do pracy w układach energoelektronicznych). | Ze względu na możliwość zmiany stanu pracy elementu dzielimy przyrządy półprzewodnikowe na sterowalne i niesterowalne, a z punktu widzenia energetycznego na przyrządy małej mocy (sygnałowe) i przyrządy mocy (do pracy w układach energoelektronicznych). | ||
| Linia 522: | Linia 530: | ||
M. P. Kaźmierkowski, J. T. Matysik: Wprowadzenie do elektroniki i energoelektroniki, | M. P. Kaźmierkowski, J. T. Matysik: Wprowadzenie do elektroniki i energoelektroniki, | ||
Oficyna Wydawnicza PW, Warszawa 2005 | Oficyna Wydawnicza PW, Warszawa 2005 | ||
J. Jaczewski, A. Opolski, J. Stolz: Podstawy elektroniki i energoelektroniki, | J. Jaczewski, A. Opolski, J. Stolz: Podstawy elektroniki i energoelektroniki, | ||
WNT, Warszawa 1981 | WNT, Warszawa 1981 | ||
P. E. Gray, C. L. Searle: Podstawy elektroniki, PWN, Warszawa 1976 | P. E. Gray, C. L. Searle: Podstawy elektroniki, PWN, Warszawa 1976 | ||
|} | |} | ||
Wersja z 10:56, 16 sty 2007
 |
Podstawy fizyczne działania elementów półprzewodnikowych. |
 |
Tabela. Podstawowe materiały półprzewodnikowe |
 |
Przykłady defektów sieci krystalicznej |
 |
Obszar, w którym zachodzi bardzo silna (o kilka rzędów wielkości) zmiana koncentracji ładunku nazywa się złączem.
Szerokość złącza ma na ogół wymiar rzędu .
|
 |
Przy niewielkich odchyleniach koncentracji nośników od stanu równowagi wypadkowa gęstość prądu elektronów i dziur jest równa:
|
| Literatura
M. P. Kaźmierkowski, J. T. Matysik: Wprowadzenie do elektroniki i energoelektroniki, Oficyna Wydawnicza PW, Warszawa 2005 J. Jaczewski, A. Opolski, J. Stolz: Podstawy elektroniki i energoelektroniki, WNT, Warszawa 1981 P. E. Gray, C. L. Searle: Podstawy elektroniki, PWN, Warszawa 1976 |