TTS Moduł 3: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
| Linia 3: | Linia 3: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd1.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd1.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|W poprzednim module zajmowaliśmy się falą płaską rozchodzącą się w nieograniczonej przestrzeni, która jest ważnym rodzajem fali elektromagnetycznej w zastosowaniach telekomunikacyjnych bo występuje pomiędzy antenami nadawczą i odbiorczą. | ||
Niemniej istotne jest rozchodzenie się fal elektromagnetycznych we wszelkiego rodzaju liniach transmisyjnych, w których fale prowadzone są w określonym kierunku. Linie te nazywamy '''prowadnicami falowymi'''. | |||
W module 3 poznamy fale elektromagnetyczne w podstawowych prowadnicach falowych stosowanych w technice pasm radiowych i mikrofalowych. Przedstawimy własności i parametry tych fal podkreślając różnice z falą płaską. Wprowadzimy podstawowe parametry obwodowe prowadnicy falowej (napięcie, prąd, impedancję charakterystyczną), które będą przydatne w szeregu zagadnieniach omawianych w kolejnych wykładach. | |||
|} | |} | ||
| Linia 11: | Linia 16: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd2.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd2.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Rozpoczniemy od klasyfikacji fal elektromagnetycznych ze wskazaniem prowadnic falowych, w których się rozchodzą. | ||
Ponieważ w strukturze prowadnicy występują dielektryki i przewodniki, należy omówić warunki brzegowe pól na granicy tych ośrodków. Znajomość tych warunków jest niezwykle istotna przy wyznaczaniu pól elektromagnetycznych w prowadnicach falowych. | |||
W dalszej części przedstawione zostaną podstawowe prowadnice falowe stosowane do transmisji sygnałów na odległości od ułamka metra do setek metrów w zakresie fal radiowych i mikrofalowych, czyli linia współosiowa oraz falowody prostokątny i kołowy. Poznamy struktury tych linii, własności fal w nich propagowanych, rozkłady pól elektromagnetycznych podstawowych rodzajów i parametry obwodowe linii. | |||
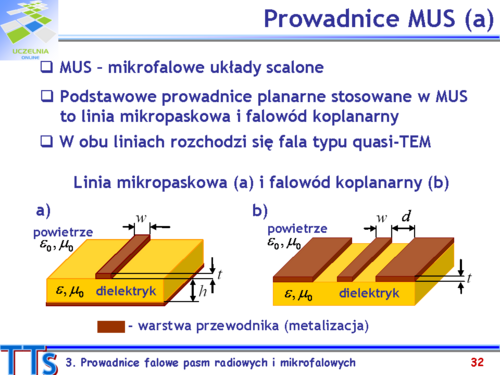
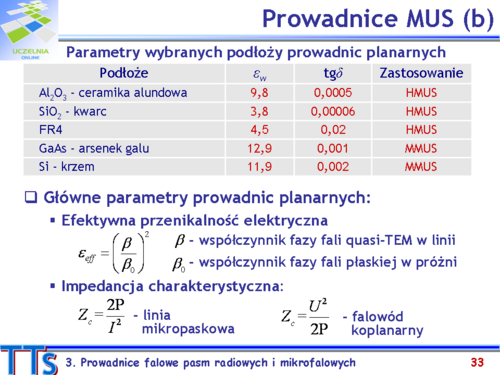
Podzespoły pracujące w pasmach mikrofalowych i stosowane w systemach radiokomunikacji realizowane są powszechnie jako mikrofalowe układy scalone (w skrócie: MUS). Charakterystyczną cechą tych układów jest występowanie prowadnicy falowej pomiędzy elementami o stałych skupionych (diody, tranzystory, rezystory, kondensatory). Poznamy dwie podstawowe prowadnice MUS: linię mikropaskową i falowód koplanarny. | |||
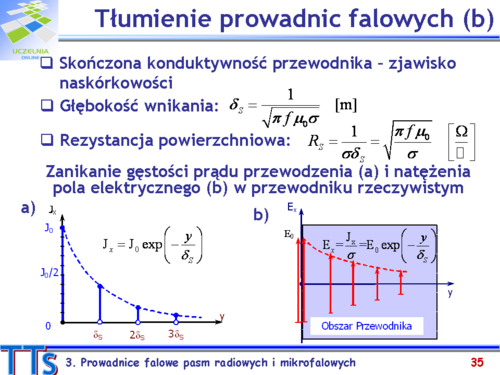
Dla celów analizy prowadnic falowych przyjmuje się, że występujące w nich przewodniki są idealne. To założenie znakomicie upraszcza proces wyznaczania pola elektromagnetycznego w linii, ale nie pozwala na obliczenie tłumienia fali. Rzeczywiste przewodniki są istotnym źródłem strat mocy fali. Z punktu widzenia transmisji sygnałów tłumienie fali w prowadnicy jest ważnym zjawiskiem i zajmiemy się nim na zakończenie tego modułu. | |||
|} | |} | ||
| Linia 20: | Linia 34: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd3.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd3.png|thumb|500px]] | ||
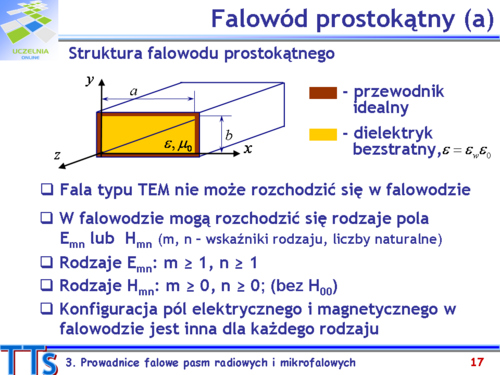
|valign="top"| | |valign="top"|Prowadzenie fal uzyskuje się wzdłuż określonego układu przewodników lub dielektryków (tzn. w obszarach cylindrycznych, których granicę są przewodzące lub są to granice dwóch dielektryków, ewentualnie odpowiednia kombinacja wymienionych materiałów). W przypadku prowadzenia fal wzdłuż przewodników, możliwe jest rozchodzenie się energii elektromagnetycznej w liniach składających się z dwóch lub więcej przewodów, a także w rurach (najczęściej o przekroju prostokątnym albo kołowym), które nie zawierają wewnątrz dodatkowych przewodników, tzw. falowodach. Natomiast przykładem prowadnicy falowej będącej układem warstw dielektrycznych jest światłowód, bez którego trudno wyobrazić sobie dzisiejszą telekomunikację. | ||
Fale w prowadnicach falowych nie muszą być falami typu TEM, tzn. mogą one mieć składowe pól elektrycznego i magnetycznego wzdłuż kierunku rozchodzenia się fali. Wprowadzić należy klasyfikację możliwych rodzajów fal nazywanych również modami. | |||
Przyjmijmy, że fala rozchodzi się zgodnie z kierunkiem osi z i wtedy wyróżnia się następujące typy fal: | |||
*fala typu TEM (poprzeczna elektryczna-magnetyczna, z ang. Transverse Electric-Magnetic): | |||
:<math>E_z = 0</math> – pole elektryczne leży w płaszczyźnie prostopadłej do kierunku propagacji fali (wektor natężenia pola elektrycznego ma co najwyżej dwie składowe), | |||
:<math>H_z = 0</math> – pole magnetyczne leży w płaszczyźnie prostopadłej do kierunku propagacji fali(wektor natężenia pola magnetycznego ma co najwyżej dwie składowe); | |||
*fala typu E (określana też TM – poprzeczna magnetyczna, z ang. Transverse Magnetic): | |||
:<math>E_z \neq 0</math> – niezerowa składowa pola elektrycznego w kierunku rozchodzenia się fali (może mieć trzy składowe), | |||
:<math>H_z = 0</math> – pole magnetyczne leży w płaszczyźnie prostopadłej do kierunku propagacji fali; | |||
*fala typu H (określana też TE – poprzeczna elektryczna, z ang. Transverse Electric): | |||
:<math>H_z \neq 0</math> – niezerowa składowa pola magnetycznego w kierunku rozchodzenia się fali (może mieć trzy składowe), | |||
:<math>E_z = 0</math> – pole elektryczne leży w płaszczyźnie prostopadłej do kierunku propagacji fali; | |||
*fala typu EH: <math>E_z \neq 0</math>, <math>H_z \neq 0</math>. | |||
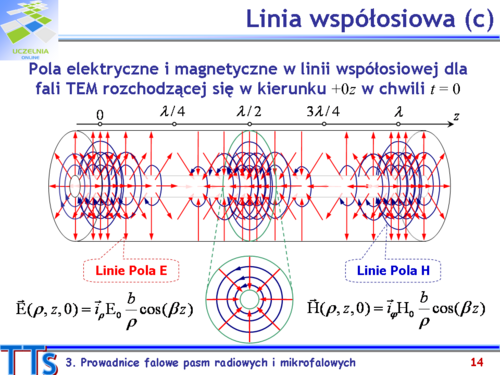
Z powyższego wykazu wynika, że tylko pierwszy z wymienionych typów fal jest falą poprzeczną. Prowadnice falowe, w których mogą rozchodzić się rodzaje TEM nazywamy liniami TEM lub prowadnicami TEM. Struktura prowadnicy TEM musi zawierać co najmniej dwa przewody. Przykładem linii TEM jest linia współosiowa, tzw. kabel koncentryczny. | |||
Fale E i H rozchodzą się w falowodach. Falowody stosuje się do prowadzenia fali elektro-magnetycznej z mniejszymi stratami niż w linii TEM (np. w transponderach satelitów telekomunikacyjnych) lub do przesyłania dużych mocy, których przesłanie nie jest możliwe linią współosiową (np. w radarach). | |||
Fale typu EH występują między innymi w falowodach dielektrycznych i światłowodach. | |||
|} | |} | ||
| Linia 28: | Linia 63: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd4.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd4.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Określenie postaci fali elektromagnetycznej w prowadnicy falowej wiąże się z poszukiwaniem rozwiązań równań Maxwella, które jest zagadnieniem matematycznym innego typu niż w przypadku fali w nieograniczonej przestrzeni. Ze względu na to, że mamy tu do czynienia z obszarem cylindrycznym o granicy przewodzącej lub w formie granicy dwóch dielektryków, musimy teraz uwzględnić warunki brzegowe. W konsekwencji pewne własności fal elektromagnetycznych w prowadnicach są inne niż fali płaskiej. | ||
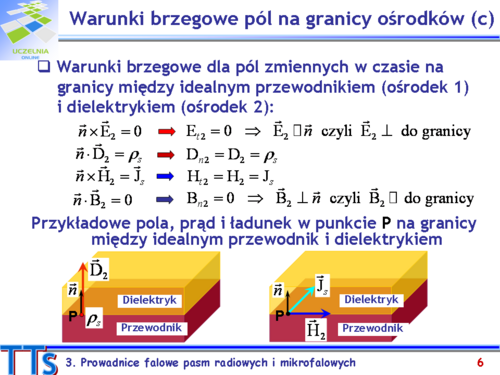
Pola elektryczne i magnetyczne w otoczeniu obustronnym granicy ośrodków muszą spełniać równania Maxwella, muszą więc być spełnione pewne wzajemne relacje między polami po obu stronach granicy ośrodków oraz występującymi na granicy prądami i ładunkami elektrycznymi. Relacje te nazywamy ''warunkami brzegowymi'' i można wyprowadzić je z równań Maxwella. | |||
Na rysunku przedstawiono pola, prąd i ładunek, które rozpatruje się w warunkach brzegowych. Wszystkie te wielkości mogą, w ogólnym przypadku, występować w jednym punkcie granicznym. Pokazana na rysunku granica jest takim „rozciągniętym punktem”. Parametry obu ośrodków są liczbami, czyli są one liniowe, jednorodne i izotropowe. | |||
W ośrodku 1, w pewnym punkcie na granicy z ośrodkiem 2, występuje pole elektryczne i związene z nim wektory <math>\vec{D}_1=\varepsilon_1\vec{E}_1</math> oraz pole magnetyczne i wektory <math>\vec{B}_1=\mu_1\vec{H}_1</math> . W tym samym punkcie granicznym w ośrodku 2 mamy pola <math>\vec{D}_2=\varepsilon_2\vec{E}_2</math> i <math>\vec{B}_2=\mu_2\vec{H}_2</math> . Przyjmijmy również, że w omawianym punkcie płaszczyzny rozgraniczającej ośrodki może występować wektor gęstości prądu powierzchniowego <math>\vec{J}_s</math>, którego miarą jest Amper na metr [A/m], oraz istnieje ładunek o gęstości powierzchniowej <math>\rho_s\, [C/m^2]</math>. | |||
Należy zauważyć, że dowolny wektor pola elektrycznego w ośrodku 1 można przedstawić w dowolnym punkcie na granicy jako sumę wektorową składowej stycznej <math>E_{t1}\,</math> oraz składowej normalnej <math>E_{n1}\,</math> do granicy rozdziału ośrodków. Analogicznie wyraża się pozostałe wektory w ośrodku 1, czyli <math>\vec{D}_1</math> , <math>\vec{H}_1</math>, <math>\vec{B}_1</math> oraz pola w ośrodku 2, co schematycznie ilustruje rysunek (na tym rysunku zaznaczono tylko składowe istotne dla warunków brzegowych oraz wersor <math>\vec{n}\,</math> normalny do granicy ośrodków). | |||
Sformułujmy warunki, które spełniają pola elektryczne i magnetyczne na granicy dwóch ośrodków. | |||
Warunki brzegowe dla pola elektrycznego: | |||
*<math>E_{t2} = E_{t1}</math> – składowa styczna wektora natężenia pola elektrycznego jest ciągła na granicy dwóch ośrodków; | |||
*<math>D_{n2} - D_{n1} = \rho_s</math> – składowa normalna wektora indukcji elektrycznej jest ciągła na granicy dwóch ośrodków z wyjątkiem przypadku, gdy na granicy istnieje ładunek powierzchniowy i wtedy doznaje ona skokowej zmiany o wartość gęstości powierzchniowej ładunku. | |||
Warunki brzegowe dla pola magnetycznego: | |||
*<math>|H_{t2} - H_{t1}|= |J_s|</math> – składowa styczna wektora natężenia pola magnetycznego jest ciągła z wyjątkiem przypadku, gdy na powierzchni granicznej występuje prąd. W tym ostatnim przypadku składowa styczna natężenia pola magnetycznego zmienia skokowo wartość na granicy ośrodków o wartość gęstości prądu powierzchniowego; | |||
|} | |} | ||
Wersja z 12:04, 8 sty 2007
Wykład
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Pytania sprawdzające
(jeśli potrafisz na nie odpowiedzieć, to znaczy, że opanowałeś/aś materiał wykładu)
- Wymień i scharakteryzuj najważniejsze parametry prowadnicy falowej.
- Przypomnij sobie jakie mody mogą rozchodzić się w falowodach i scharakteryzuj je.
- Co to jest dyspersja, w jakich warunkach i dlaczego dyspersja utrudnia transmisję sygnału.
- Przeanalizuj przyczyny powstawania strat przy transmisji mocy prowadnicami falowymi.
- Na czym polega efekt naskórkowości?
- Opisz kolejno prowadnice typu TEM.
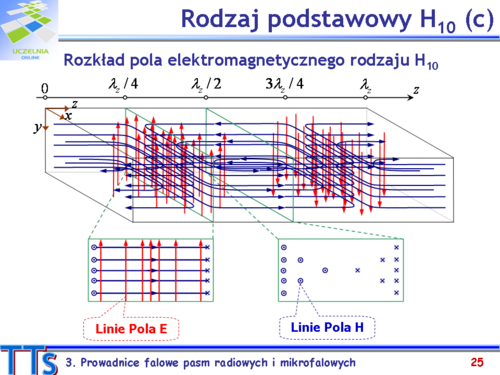
- Narysuj konfigurację pól E i H dla modu podstawowego i naszkicuj kierunki przepływu prądów w ściankach falowodu prostokątnego.
- Dlaczego nie stosujemy falowodów prostokątnych, dla których stosunek a/b=1?
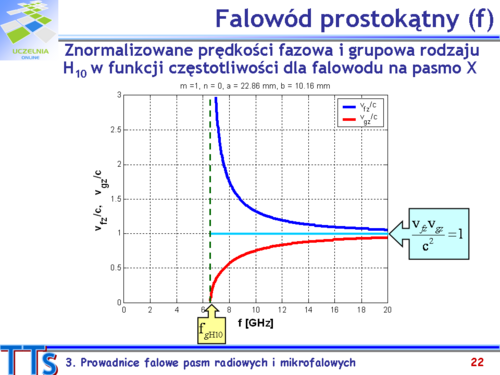
- W jakim pasmie częstotliwości może pracować falowód prostokątny?
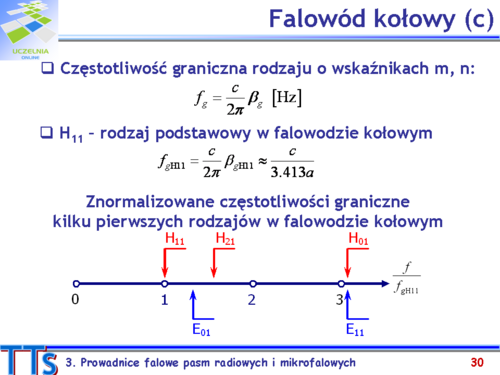
- W jakim pasmie może pracować falowód cylindryczny?
- Jak uzasadnisz fakt, że obwodem zastępczym odcinka falowodu prostokątnego jest odcinek linii dwuprzewodowej?
- Jak zbudowana jest i jakie ma właściwości prowadnica mikropaskowa?
- Jak zbudowana jest i jakie ma właściwości linia koplanarna?
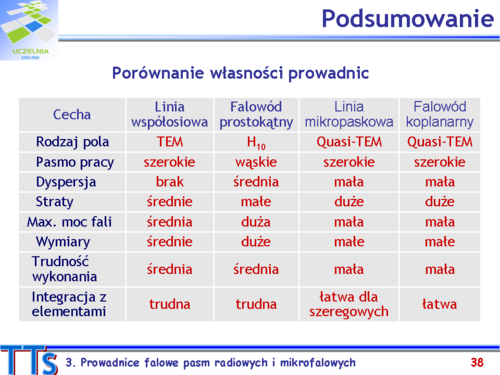
- Jakie są obszary zastosowań linii współosiowej, linii mikropaskowej i falowodu prostokątnego? Aby to uzasadnić porównaj parametry wymienionych typów prowadnic.
- Wymień argumenty przemawiające za rozwojem technologii i konstrukcji Mikrofalowych Monolitycznych Układów Scalonych na krzemie i arsenku galu.
Słownik
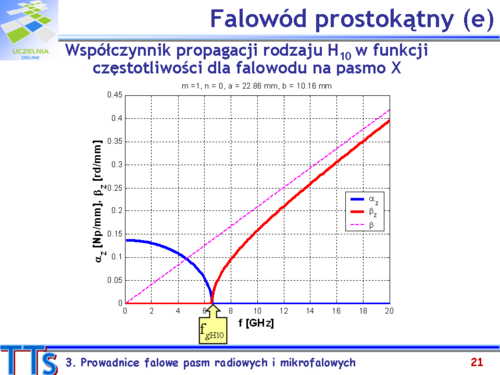
Częstotliwość graniczna - częstotliwość powyżej której może się propagować fala w falowodzie. Poniżej tej częstotliwości fala jest silnie tłumiona.
Zestawienie typów fal:
- Fala typu TEM - wektory pola E i H leżą w płaszczyźnie prostopadłej do kierunku propagacji.
- Fala typu TE (zwana też H) - pole E posiada składowe tylko w płaszczyźnie prostopadłej do kierunku propagacji. Pole H posiada składowe w kierunku propagacji fali.
- Fala typu TM (zwana też E) - pole H posiada składowe tylko w płaszczyźnie prostopadłej do kierunku propagacji. Pole E posiada składowe w kierunku propagacji fali.
- Fala typu EH - zarówno pole E jak i pole H tej fali posiadają składowe w kierunku propagacji.
Linie TEM:
- Linia współosiowa.
- Linia dwuprzewodowa.
- Symetryczna linia paskowa.
Linie Quasi-TEM:
- Niesymetryczna linia paskowa:
- Linia koplanarna (falowód koplanarny).
- Linia koplanarna paskowa.
Linie falowodowe:
- Falowód prostokątny. Mod podstawowy typu TE10 (H10).
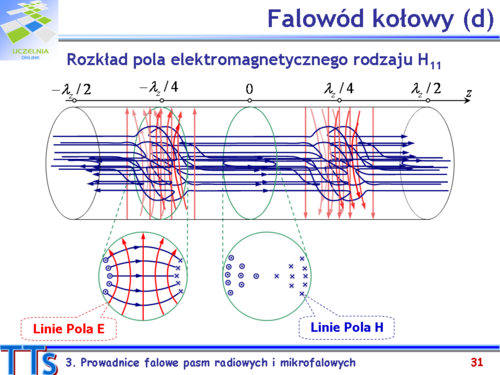
- Falowód kołowy (cylindryczny). Mod podstawowy typu TE11 (H11).
Mod (rodzaj) podstawowy dla danego falowodu - to mod fali o najmniejszej
Bibliografia
- Bogdan Galwas. Miernictwo mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1985, Rozdział 1, 2 i 3.
- Tadeusz Morawski, Wojciech Gwarek. Pola i fale elektromagnetyczne, Wydawnictwa Naukowo-Techniczne, Warszawa, 1998, Rozdział 1 do 8.
- Janusz Dobrowolski. Technika wielkich częstotliwości, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa, 1998 Rozdział 1 i 3.
- Stanisław Rosłoniec. Liniowe obwody mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1999, Rozdział 2.



