|
|
| Linia 18: |
Linia 18: |
| <hr width="100%"> | | <hr width="100%"> |
|
| |
|
| *'''PROWADNICE TEM'''
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd3.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| :*'''Właściwości prowadnic TEM'''
| | |} |
|
| |
|
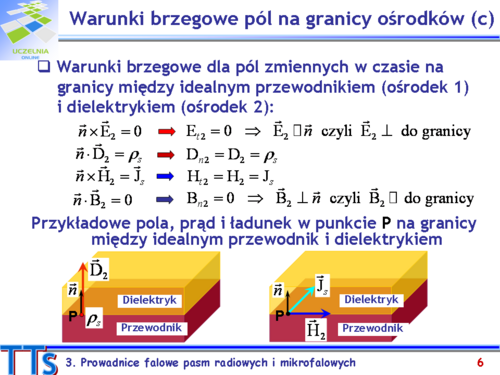
| Można wykazać, że zależności pól w prowadnicy TEM od zmiennej z są identyczne jak dla fali płaskiej w przestrzeni nieograniczonej. Podobnie możemy uzyskać równanie falowe określające wektory <math>E_T\,</math> lub <math>H_T\,</math> w postaci. Oznacza to, że wektory pól <math>E\,</math> i <math>H\,</math> są do siebie prostopadłe i prostopadłe do kierunku propagacji <math>z\,</math>.
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd4.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| :{| width="100%"
| |
| | width="95%" align="left" | <math>\displaystyle \gamma=\sqrt{j\omega \mu (\sigma +j\omega \varepsilon)}=\alpha +j\beta</math>
| |
| | align="right" | ''(3-1)''
| |
| |} | | |} |
|
| |
|
| Dodatkowo, relacje między wektorami pól elektrycznego i magnetycznego obowiązują dla prowadnic TEM, czyli
| | <hr width="100%"> |
|
| |
|
| :{| width="100%"
| | {| border="0" cellpadding="4" width="100%" |
| | width="95%" align="left" | <math>\displaystyle E_T=Z_fH_T\times i_z</math> | | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd5.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| <math>\displaystyle H_T=\frac{1}{Z_f} i_z\times E_T</math>
| |
| | align="right" | ''(3-2)''
| |
| |} | | |} |
|
| |
|
| oraz spełniona jest poniższa relacja
| | <hr width="100%"> |
| | |
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd6.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| :{| width="100%"
| |
| | width="95%" align="left" | <math>\displaystyle Z_f=Z_w=\sqrt{\frac{j\omega \mu}{\sigma +j\omega \varepsilon}}</math>
| |
| | align="right" | ''(3-3)''
| |
| |} | | |} |
|
| |
|
| Zasadnicza różnica między cechami pół fali płaskiej w ośrodku nieograniczonym i pól w linii TEM jest związana z tym, że pola w ośrodku nieograniczonym nie zależą od zmiennych w płaszczyźnie prostopadłej do kierunku rozchodzenia się fali, natomiast w prowadnicy TEM, w której muszą być spełnione określone warunki brzegowe na powierzchni przewodników linii, pola na ogół zależą od tych zmiennych.
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd7.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| Warto zapamiętać, że prowadnicę falową charakteryzują dwa parametry: współczynnik propagacji <math>\gamma\,</math> oraz impedancja charakterystyczna <math>Z_0\,</math>. Pierwszy z tych parametrów jest wielkością polową, której obliczenie wiąże się w ogólności z rozwiązaniem równań Maxwella. Drugi jest wielkością obwodową, wyznaczaną z zastosowaniem definicji (3-4):
| |
|
| |
| :{| width="100%"
| |
| | width="95%" align="left" | <math>\displaystyle Z_0=\frac{U}{I}</math>
| |
| | align="right" | ''(3-4)''
| |
| |} | | |} |
|
| |
|
| w której <math>U\,</math> i <math>I\,</math> są amplitudami napięcia i prądu fali poruszającej się w jedną stronę.
| | <hr width="100%"> |
|
| |
|
| Definicja <math>Z_0\,</math> jest przydatna przy analizie obwodów zawierających prowadnice falowe i elementy reprezentowane przez układy zastępcze o stałych skupionych.
| | {| border="0" cellpadding="4" width="100%" |
|
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd8.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| :*'''Linia współosiowa'''
| | |} |
|
| |
|
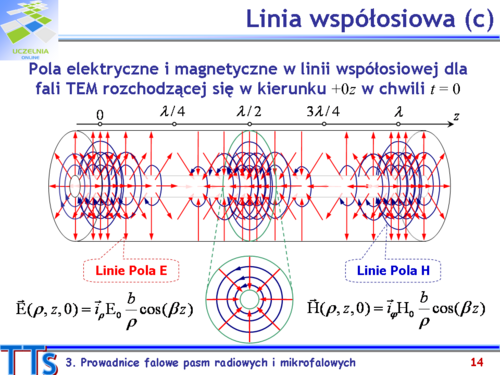
| Najpopularniejszą prowadnicą w rodzinie TEM jest linia współosiowa o promieniach <math>a\,</math> i <math>b\,</math> (<math>a>b</math>), w której przestrzeń między przewodem wewnętrznym i zewnętrznym wypełniona jest małostratnym dielektrykiem o przenikalności względnej <math>\varepsilon_r\,</math> – rys.3.1. Impedancja charakterystyczna linii współosiowej obliczana jest z zależności:
| | <hr width="100%"> |
|
| |
|
| :{| width="100%"
| | {| border="0" cellpadding="4" width="100%" |
| | width="95%" align="left" | <math>\displaystyle Z_0[\Omega]=\frac{138}{\sqrt{\varepsilon_r}}log\frac{b}{a}</math> | | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd9.png|thumb|500px]] |
| | align="right" | ''(3-5)'' | | |valign="top"| |
| |}
| |
|
| |
|
| {| border="1" cellpadding="5" cellspacing="0" align="center"
| |
| |-
| |
| ! Rys.3.1. Przekrój poprzeczny
| |
| linii współosiowej .
| |
| ||[[Grafika:TTS_M3_Rys1.png]]
| |
| |-
| |
| |} | | |} |
|
| |
|
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd10.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| Zależność (3-5) wskazuje, że impedancja charakterystyczna linii współosiowej zależy od stosunku promieni przewodów i właściwości ośrodka wypełniającego prowadnicę.
| | |} |
|
| |
|
| Linia współosiowa, albo koncentryczna jest szeroko stosowana w systemach pomiarowych, a rozpowszechnionym w aparaturze standardem jest linia o impedancji <math>Z_0=50\,\Omega</math>. Linie współosiowe pracują do 60 GHz.
| | <hr width="100%"> |
|
| |
|
| Tłumienie linii współosiowej jest najmniejsze dla <math>Z_0=75\,\Omega</math>, ten standard przyjęto w telekomunikacji (m.in. sieci telewizji kablowej).
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd11.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| | |} |
|
| |
|
| :*'''Linia dwuprzewodowa'''
| | <hr width="100%"> |
|
| |
|
| Na rys.3.2 przedstawiono strukturę innej linii TEM, a mianowicie linii dwuprzewodowej. Przewody zanurzone są w dielektryku o przenikalności <math>\varepsilon_r\,</math>. Polowe wielkości charakteryzujące falę TEM dla tej prowadnicy są identyczne jak dla linii współosiowej. Impedancję charakterystyczną linii dwuprzewodowej określa zależność:
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd12.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| :{| width="100%"
| |
| | width="95%" align="left" | <math>\displaystyle Z_0[\Omega]=\frac{276}{\sqrt{\varepsilon_r}}log\frac{s}{a}</math>
| |
| | align="right" | ''(3-6)''
| |
| |} | | |} |
|
| |
|
| Linia dwuprzewodowa jest z historycznego punktu widzenia pierwszą linią długą, dla której znaleziono rozwiązanie falowe. Stosowana jest jeszcze w sieciach telewizyjnych i telefonicznych w postaci tzw. skrętki.
| | <hr width="100%"> |
| | |
|
| |
|
| {| border="1" cellpadding="5" cellspacing="0" align="center" | | {| border="0" cellpadding="4" width="100%" |
| |- | | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd13.png|thumb|500px]] |
| ! [[Grafika:TTS_M3_Rys2.png]] || [[Grafika:TTS_M3_Rys3.png]]
| | |valign="top"| |
| |- | |
| | colspan="3" align="center"| '''Rys.3.2. Przekroje poprzeczne przykładowych prowadnic TEM:'''
| |
|
| |
|
| '''linii dwuprzewodowej (a) i symetrycznej linii paskowej (b).'''
| |
| |} | | |} |
|
| |
|
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd14.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| :*'''Symetryczna linia paskowa'''
| |
|
| |
| Strukturę symetrycznej linii paskowej pokazano na rys.3.2b. Impedancję charakterystyczną tej linii oblicza się ze wzoru:
| |
|
| |
| :{| width="100%"
| |
| | width="95%" align="left" | <math>\displaystyle Z_0[\Omega]=\frac{30\pi }{\sqrt{\varepsilon_r}}\frac{b}{w+0,441b}</math>
| |
| | align="right" | ''(3-7)''
| |
| |} | | |} |
|
| |
|
| Symetryczna linia paskowa stosowana w konstrukcjach niektórych przyrządów, jak sprzęgacze, filtry, itp..
| | <hr width="100%"> |
|
| |
|
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd15.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| *'''FALOWÓD PROSTOKĄTNY'''
| | |} |
|
| |
|
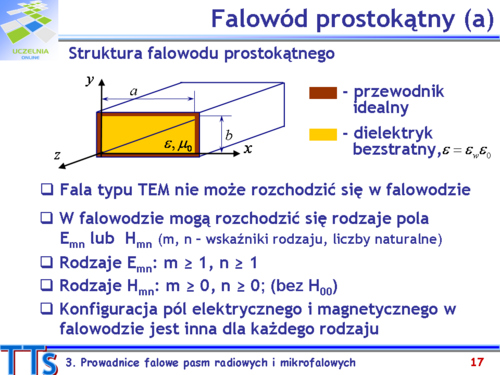
| Zgodnie z pokazaną na rys.3.3 strukturą falowód prostokątny jest prowadnicą falową, w której nie występują dwa niezależne przewody, a więc nie może się rozchodzić fala elektromagnetyczna typu TEM.
| | <hr width="100%"> |
|
| |
|
| Mogą natomiast, przy spełnieniu pewnych warunków rozchodzić mody TE (E) lub TM (H). Dla każdego z modów konfiguracja pól E i H jest inna. Można udowodnić, że dla każdego modu można określić częstotliwość graniczną, poniżej której dany mod nie może zostać wzbudzony.
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd16.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
|
| |
| {| border="1" cellpadding="5" cellspacing="0" align="center"
| |
| |-
| |
| !Rys.3.3 Struktura i wymiary
| |
| falowodu prostokątnego
| |
| ||[[Grafika:TTS_M3_Rys4.png]]
| |
| |-
| |
| |} | | |} |
|
| |
|
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd17.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| Każdy z modów określony jest wskaźnikami „m” i „n”. Wartość częstotliwości granicznej zależy od wartości „m” i „n”, od rozmiarów a i b falowodu, oraz od wartości przenikalności elektrycznej materiału wypełniającego falowód. W miarę wzrostu częstotliwości wzbudzają się kolejne mody <math>TE_{m,n}\,</math> i <math>TM_{m,n}\,</math>. Mod o najniższej częstotliwości granicznej nazywany jest podstawowym. Modem podstawowym w falowodzie prostokątnym jest TE10. Dla niego wartość długości fali granicznej (jest to długość fali w wolnej przestrzeni dla częstotliwości granicznej) wynosi:
| |
|
| |
| :{| width="100%"
| |
| | width="95%" align="left" | <math>\displaystyle \lambda_{gTE10}=2a</math>
| |
| | align="right" | ''(3-8)''
| |
| |} | | |} |
|
| |
|
| | <hr width="100%"> |
|
| |
|
| W Tabeli 3.1 zestawiono wartości częstotliwości granicznych dla kilku pierwszych modów, dla falowodu skonstruowanego do pracy w pasmie <math>3\, cm\,</math>, bez wypełnienia dielektrykiem.
| | {| border="0" cellpadding="4" width="100%" |
| | | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd18.png|thumb|500px]] |
| | | |valign="top"| |
| '''Tabela 3.1:''' Pierwsze mody falowodu na pasmo X, o wymiarach: <math>a=2,286\, cm</math>, <math>b=1,016\, cm</math>.
| |
| | |
| {| border="1" cellpadding="5" cellspacing="0" align="center" | |
| !MOD ||<math>TE_{10}\,</math> || <math>TE_{20}\,</math> || <math>TE_{01}\,</math> || <math>TE_{11}TM_{11}\,</math>
| |
| |- | |
| !Częstotliwość graniczna <math>f_g[GHz]\,</math> ||<math>6,562\,</math> || <math>13,123\,</math> || <math>14,764\,</math> || <math>16,156\,</math>
| |
| |- | |
|
| |
|
| |} | | |} |
|
| |
|
| | <hr width="100%"> |
|
| |
|
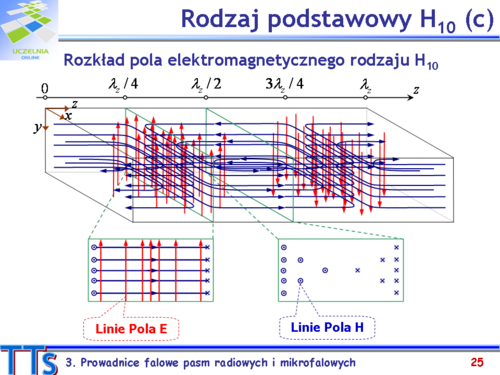
| Rozkład pola elektrycznego i magnetycznego dla modu <math>TE_{10}\,</math> pokazano na rys.3.4.
| | {| border="0" cellpadding="4" width="100%" |
| | | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd19.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| {| border="1" cellpadding="5" cellspacing="0" align="center"
| |
| |-
| |
| !Rys.3.4. Linie sił pola elektrycznego E
| |
| i magnetycznego H dla modu podstawowego
| |
| ||[[Grafika:TTS_M3_Rys5.png]]
| |
| |-
| |
| |} | | |} |
|
| |
|
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd20.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| Pasmo pracy falowodu prostokątnego zawiera się między częstotliwością graniczą modu podstawowego i częstotliwością graniczną kolejnego modu, z pewnymi marginesami.
| |
|
| |
| Prędkości: fazowa <math>v_f\,</math> i grupowa <math>v_g\,</math> oraz długość fali <math>\lambda_f\,</math> są, dla tej samej <math>f\,</math> różne i różne dla różnych modów. Oznaczamy: prędkość <math>v\,</math> i długość <math>\lambda\,</math> dla fali płaskiej w wolnej przestrzeni wypełnionej ośrodkiem o <math>\varepsilon_r \varepsilon_0\,</math> i <math>\mu_r \mu_0\,</math>.
| |
|
| |
| :{| width="100%"
| |
| | width="95%" align="left" | <math>\displaystyle v=\frac{c}{\sqrt{\mu_r \varepsilon_r}};\, \displaystyle \lambda=\frac{\lambda_0}{\sqrt{\mu_r \varepsilon_r}}</math>
| |
| | align="right" | ''(3-9)''
| |
| |} | | |} |
|
| |
|
| Dla falowodów prędkość fazowa i długość fali w falowodzie opisują następujące zależności:
| | <hr width="100%"> |
|
| |
|
| :{| width="100%"
| | {| border="0" cellpadding="4" width="100%" |
| | width="95%" align="left" | <math>\displaystyle v_f=\frac{\omega}{\beta}=\frac{v}{\sqrt{1-(f_{gmn}/f)^2}}</math> | | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd21.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| <math>\displaystyle v_g=v\sqrt{1-(f_{gmn}/f)^2}=\frac{1}{d\beta/d\omega}</math>
| |
| | align="right" | ''(3-10)''
| |
| |} | | |} |
|
| |
|
| Długość fali <math>\lambda\,</math> w falowodzie jest większa, niż w wolnej przestrzeni i gdy częstotliwość zbliża się do częstotliwości granicznej długość fali rośnie do nieskończoności.
| | <hr width="100%"> |
|
| |
|
| :{| width="100%"
| | {| border="0" cellpadding="4" width="100%" |
| | width="95%" align="left" | <math>\displaystyle \lambda_f=\frac{\lambda}{\sqrt{1-(f_{gmn}/f)^2}}</math> | | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd22.png|thumb|500px]] |
| | align="right" | ''(3-11)'' | | |valign="top"| |
| |}
| |
|
| |
|
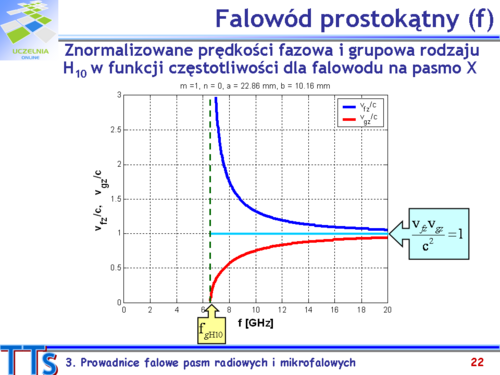
| Między prędkościami fazową i grupową istnieje związek (3-12):
| |
|
| |
| :{| width="100%"
| |
| | width="95%" align="left" | <math>\displaystyle v_gv_f=v^2</math>
| |
| | align="right" | ''(3-12)''
| |
| |} | | |} |
|
| |
|
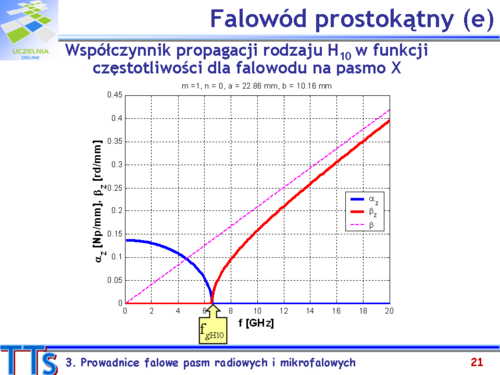
| Na rys.3.5 pokazano zależności <math>v_f(f/f_g)\,</math> i <math>v_g(f/f_g)\,</math>. Gdy częstotliwość zbliża się do wartości granicznej, to prędkość fazowa rośnie do nieskończoności, prędkość grupowa maleje do zera i ustaje przepływ energii. Poniżej częstotliwości granicznej dany mod nie może zostać wzbudzony.
| | <hr width="100%"> |
|
| |
|
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd23.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| {| border="1" cellpadding="5" cellspacing="0" align="center"
| |
| |-
| |
| !Rys.3.5. Prędkości fazowa
| |
| i grupowa w falowodzie
| |
| ||[[Grafika:TTS_M3_Rys6.png]]
| |
| |-
| |
| |} | | |} |
|
| |
|
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd24.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| Straty mocy w ściankach metalowych powodują, że falowody wykazują stosunkowo duże tłumienie mocy sygnału. Aby je zmniejszyć falowody prostokątne wykonywane są z miedzi, mosiądzu, aluminium, często są srebrzone i złocone.
| |
|
| |
|
| |
| *'''FALOWÓD CYLINDRYCZNY'''
| |
|
| |
| Falowód cylindryczny jest metalową rurą, najczęściej powietrzną, co pokazuje rys.3.6a.
| |
| W falowodzie cylindrycznym można także wzbudzić nieskończenie wiele modów <math>TE_{m,n}\,</math> i <math>TM_{m,n}\,</math>.
| |
|
| |
| Wartość częstotliwości granicznej <math>f_{gmn}\,</math> związana jest z wartościami:
| |
|
| |
| *dla modów <math>TM_{nm}\,</math> z m-tym pierwiastkiem funkcji Bessela <math>J_n(x)=0</math>,
| |
| *dla modów <math>TE_{nm}\,</math> z m-tym pierwiastkiem pochodnych tych funkcji <math>J_n^{'}(x)=0</math>.
| |
|
| |
| Obecność funkcji Bessela wynika z rozwiązania równań Maxwella dla falowodu cylindrycznego.
| |
|
| |
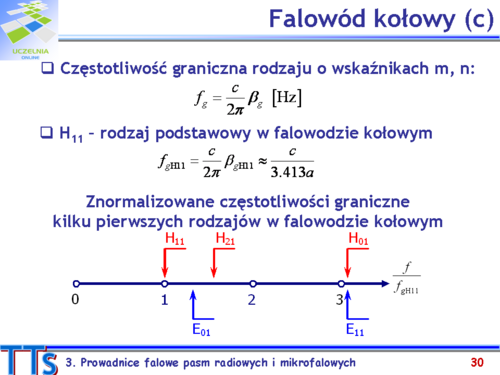
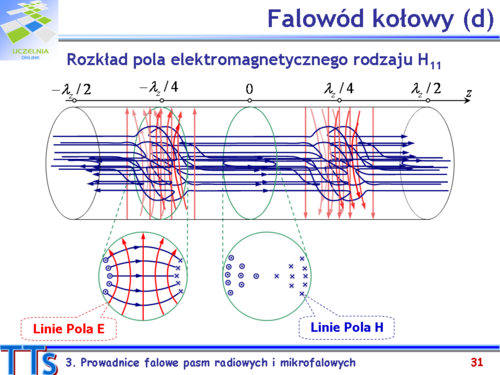
| Modem podstawowym falowodu cylindrycznego jest mod <math>TE_{11}\,</math>. Długość fali odpowiadającej częstotliwości granicznej dla tego modu równa jest:
| |
|
| |
| :{| width="100%"
| |
| | width="95%" align="left" | <math>\displaystyle \lambda_{cTE11}=3,412a</math>
| |
| | align="right" | ''(3-13)''
| |
| |} | | |} |
|
| |
|
| | <hr width="100%"> |
|
| |
|
| {| border="1" cellpadding="5" cellspacing="0" align="center" | | {| border="0" cellpadding="4" width="100%" |
| |- | | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd25.png|thumb|500px]] |
| ! [[Grafika:TTS_M3_Rys7.png]] || [[Grafika:TTS_M3_Rys8.png]]
| | |valign="top"| |
| |- | |
| | colspan="3" align="center"| '''Rys.3.6. Falowód cylindryczny. a) Wymiary falowodu cylindrycznego. '''
| |
|
| |
|
| '''b) Oś z częstotliwościami kolejnych modów.'''
| |
| |} | | |} |
|
| |
|
| | <hr width="100%"> |
|
| |
|
| Kolejny mod, który się wzbudzi, to <math>TM_{01}\,</math>, a następnie <math>TE_{21}\,</math>. tak więc pasmo pracy falowodu cylindrycznego jest niewielkie, co ogranicza zakres zastosowań. Falowody te stosowane są w konstrukcjach niektórych rezonatorów i filtrów, ze względu na ich duże dobrocie (będzie o tym mowa w jednym z dalszych wykładów).
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd26.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
|
| |
| *'''PROWADNICE MIKROFALOWYCH UKŁADÓW SCALONYCH'''
| |
|
| |
| :*'''Linia mikropaskowa'''
| |
|
| |
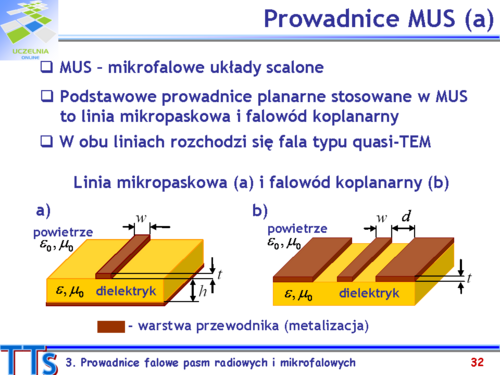
| Rozwój technologii układów scalonych, planarnych z samej natury, zmusił konstruktorów do opracowania nowej rodziny prowadnic falowych, które można stosować zarówno w hybrydowych jak i monolitycznych układach scalonych. Najpopularniejszym rozwiązaniem jest linia mikropaskowa, której strukturę pokazano na rys.3.7a. Płaska, o odpowiednio dobranej grubości h warstwa dielektryka pokrywana jest obustronnie metalem. Warstwa metalizacji jest z jednej strony pozostawiona w całości, natomiast z drugiej strony pozostawione są tylko wąskie ścieżki metalizacji o odpowiednio dobranej szerokości <math>w\,</math>.
| |
|
| |
| Linia mikropaskowa nazywana jest linią quasi-TEM, ponieważ fala EM porusza się w ośrodkach o 2 różnych prędkościach. Linia wykazują niewielka dyspersję.
| |
|
| |
|
| |
| {| border="1" cellpadding="5" cellspacing="0" align="center"
| |
| |-
| |
| ! [[Grafika:TTS_M3_Rys9.png]] || [[Grafika:TTS_M3_Rys10.png]]
| |
| |-
| |
| ! Rys.3.7. Prowadnice planarne.
| |
| a) Linia mikropaskowa
| |
|
| |
| b). Linia koplanarna
| |
|
| |
| c). Linia paskowa koplanarna.
| |
| || [[Grafika:TTS_M3_Rys11.png]]
| |
| |} | | |} |
|
| |
|
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd27.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| Impedancja charakterystyczna linii mikropaskowej jest funkcją grubości warstwy <math>h\,</math>, szerokości paska metalizacji w oraz przenikalności elektrycznej <math>\varepsilon_r\,</math> dielektryka oddzielającego pasek od metalizacji „ziemi”.
| |
|
| |
| Do zależności na prędkość i długość fali wprowadza się efektywną przenikalność <math>\varepsilon_{eff}\,</math>, której wartość leży między <math>\varepsilon_r\,</math> podłoża a <math>\varepsilon_0\,</math> powietrza. Odpowiednie zależności można znaleźć w dostępnej literaturze.
| |
|
| |
| Zakres częstotliwości pracy linii mikropaskowej jest szeroki, od prądu stałego DC do 30 GHz dla układów hybrydowych, i do 500 GHz dla układów monolitycznych.
| |
|
| |
|
| |
| :*'''Linie koplanarne'''
| |
|
| |
| Niedogodnością struktury linii mikropaskowej jest konieczność wykonywania otworów w warstwie dielektryka zwierających pasek z warstwą metalizacji. Jest to szczególnie kłopotliwe w przypadku realizacji monolitycznych układów scalonych. Niedogodności tej nie ma całkowicie planarna struktura linii koplanarnej pokazana na rys.3.7b. W niektórych rozwiązaniach stosowane także dwuprzewodowe linie planarne – rys.3.7c.
| |
|
| |
| Impedancje charakterystyczne <math>Z_0\,</math> zależy od <math>\varepsilon_r\,</math> podłoża i wymiarów linii i mogą być dobierane w szerokich granicach: dla linii mikropaskowej <math>20...100\, \Omega</math>, dla linii koplanarnej <math>25...150\, \Omega</math>, a dla linii dwuprzewodowej koplanarnej <math>45...220\, \Omega</math>.
| |
|
| |
| Dla potrzeb technologii mikrofalowych układów scalonych opracowano techniki wytwarzania planarnych rezystorów, kondensatorów, cewek indukcyjnych, a także diod i tranzystorów. W scalonych układach hybrydowych MIC elementy te montuje się na powierzchni układu, łączą je z paskami prowadnic falowych. W monolitycznych układach scalonych MMIC wszystkie elementy wykonuje się w procesach technologicznych na podłożu krzemu, albo arsenku galu.
| |
|
| |
|
| |
| :*'''Podłoża linii planarnych'''
| |
|
| |
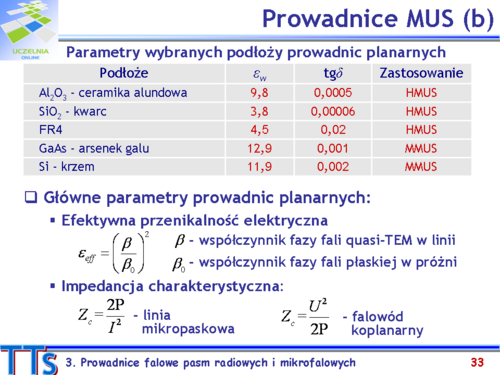
| Jak wspomniano wyżej parametry linii planarnej, takie jak impedancja charakterystyczna, długość fali, straty zależą od rodzaju użytego dielektryka. Zestawienie typowych dielektryków i ich najważniejsze parametry zestawiono w Tabeli 3.2.
| |
|
| |
|
| |
| '''Tabela 3.2.''' Zestawienie właściwości podłoży prowadnic planarnych
| |
|
| |
|
| |
| '''Tabela 3.1:''' Pierwsze mody falowodu na pasmo X, o wymiarach: <math>a=2,286\, cm</math>, <math>b=1,016\, cm</math>.
| |
|
| |
|
| |
| {| border="1" cellpadding="5" cellspacing="0" align="center"
| |
| !Podłoże ||<math>\varepsilon_r\,</math> || <math>tg\delta \,</math> || Zastosowania
| |
| |-
| |
| !<math>Al_2O_3\,</math> - ceramika alundowa || 9,6 || 0,0001 || MIC
| |
| |-
| |
| !<math>SiO_2\,</math> - kwarc || 3,8 || 0,00006 || MIC
| |
| |-
| |
| !Teflon || 2,1 || 0,00015 || MIC
| |
| |-
| |
| !<math>GaAs\,</math> - arsenek galu|| 12,5 - 13 || 0,002 || MMIC
| |
| |-
| |
| !<math>Si\,</math> - krzem|| 11,2 || 0,004 || MMIC
| |
| |-
| |
| |} | | |} |
|
| |
|
| | <hr width="100%"> |
|
| |
|
| Wśród nich najbardziej popularnymi są ceramika alundowa <math>Al_2O_3\,</math>, płytki wykonane z kwarcu oraz teflon, niekiedy wymieszany z proszkiem alundowym.
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd28.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| Arsenek galu i krzem jako półprzewodniki samoistne o niewielkim poziomie domieszek nie są najlepszymi dielektrykami i wykonane na nich linie wykazują duże straty. Jednakże stosujemy je w układach monolitycznych, gdyż tylko na takim podłożu można wykonywać aktywne tranzystory.
| |
|
| |
|
| |
| *'''TŁUMIENIE PROWADNIC FALOWYCH'''
| |
|
| |
| :*'''Straty w liniach długich'''
| |
|
| |
| Tłumienie mocy sygnału propagowanego prowadnicą falową zależy od trzech najważniejszych czynników:
| |
|
| |
| *przewodności metalu, z którego wykonano przewody linii,
| |
| *strat materiału dielektrycznego wypełniającego częściowo lub w całości prowadnicę,
| |
| *strat mocy na promieniowanie.
| |
|
| |
| Można więc w ogólnym przypadku zapisać współczynnik tłumienia następująco:
| |
|
| |
| :{| width="100%"
| |
| | width="95%" align="left" | <math>\displaystyle \alpha=\alpha_m+\alpha_d+\alpha_{rad}</math>
| |
| | align="right" | ''(3-14)''
| |
| |} | | |} |
|
| |
|
| Gdzie <math>\alpha_m\,</math> reprezentują straty wywołane skończoną przewodnością metalu, <math>\alpha_d\,</math> to straty wywołane obecnością stratnego dielektryka, a <math>\alpha_{rad}\,</math> reprezentuje straty wywołane promieniowaniem energi na zewnątrz linii.
| | <hr width="100%"> |
|
| |
|
| Przyjmiemy, że linia TEM wypełniona jest dielektrykiem o przenikalności:
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd29.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| :{| width="100%"
| |
| | width="95%" align="left" | <math>\displaystyle \varepsilon=\varepsilon' +j\varepsilon''=\varepsilon_r\varepsilon_0 (1-jtg\delta)</math>
| |
| | align="right" | ''(3-15)''
| |
| |} | | |} |
|
| |
|
| Dla linii współosiowej można oszacować straty następująco:
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd30.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| :{| width="100%"
| |
| | width="95%" align="left" | <math>\displaystyle \alpha_d=\frac{\pi tg\delta}{\lambda_f}=\frac{\pi ftg\delta}{v_f}</math>
| |
| | align="right" | ''(3-16)''
| |
| |} | | |} |
|
| |
|
| Jak widać <math>\alpha_d\,</math> rośnie proporcjonalnie do częstotliwości <math>f\,</math> we wszystkich liniach TEM i quasi-TEM.
| | <hr width="100%"> |
|
| |
|
| Ogólnie:
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd31.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| :{| width="100%"
| |
| | width="95%" align="left" | <math>\alpha_d=Aftg\delta</math>
| |
| | align="right" | ''(3-17)''
| |
| |} | | |} |
|
| |
|
| a stała proporcjonalności zależy od rozmiarów linii.
| | <hr width="100%"> |
| | |
| Straty spowodowane niedoskonałością przewodnika są duże i rosną z częstotliwością, ze względu na efekt naskórkowości. Jak nam wiadomo pole elektryczne nie wnika do doskonałego przewodnika, ale do niedoskonałego wnika, na pewną, niewielką głębokość - rys.3.8a.
| |
|
| |
|
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd32.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| {| border="1" cellpadding="5" cellspacing="0" align="center"
| |
| |-
| |
| ! [[Grafika:TTS_M3_Rys12.png]] || [[Grafika:TTS_M3_Rys13.png]]
| |
| |-
| |
| | colspan="3" align="center"| '''Rys.3.8. Zanikanie pola elektrycznego (a) i pradu (b) jako efekt naskórkowości.'''
| |
| |} | | |} |
|
| |
|
| | <hr width="100%"> |
|
| |
|
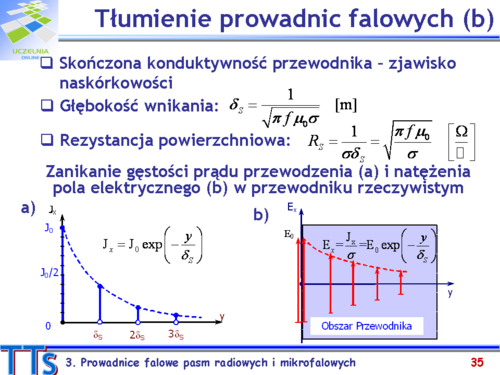
| W rezultacie na powierzchni przewodnika płynie prąd, ale tylko w cienkiej warstwie o głębokości wnikania <math>\delta_s[m]</math> i szybko zanika w warstwach głębszych – rys.3.8b. Głębokość wnikania może być obliczona ze wzoru (3-18):
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd33.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| :{| width="100%"
| |
| | width="95%" align="left" | <math>\displaystyle \delta_s[m]=\frac{1}{\sqrt{\pi f\mu_r \mu_0 \sigma}}</math>
| |
| | align="right" | ''(3-18)''
| |
| |} | | |} |
|
| |
|
| Na przykład dla miedzi <math>Cu\,</math>, dla częstotliwości <math>f = 10\, GHz</math>, głębokość wnikania jest niewielka i wynosi <math>\delta_s=0,66\mu\,m</math>.
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd34.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| Rezystancja powierzchniowa <math>R_s[\Omega/kwadrat]\</math> rośnie dla każdego przewodnika z częstotliwością <math>f\,</math>, choć wolniej dla przewodników dobrze przewodzących (duża przewodność <math>\sigma\,</math>):
| |
|
| |
| :{| width="100%"
| |
| | width="95%" align="left" | <math>\displaystyle R_s[\Omega/kw.]=\frac{1}{\sigma \delta_s}=\sqrt{\frac{\pi f\mu_r \mu_0}{\sigma}}</math>
| |
| | align="right" | ''(3-19)''
| |
| |} | | |} |
|
| |
|
| Dla linii typu TEM składnik stałej tłumienia <math>\alpha_m\,</math> jest proporcjonalny do rezystancji <math>R_s\,</math> :
| | <hr width="100%"> |
|
| |
|
| :{| width="100%"
| | {| border="0" cellpadding="4" width="100%" |
| | width="95%" align="left" | <math>\displaystyle \alpha_m=B\sqrt{\frac{f\mu_r}{\sigma}}</math> | | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd35.png|thumb|500px]] |
| | align="right" | ''(3-20)'' | | |valign="top"| |
| |}
| |
|
| |
|
| Straty na promieniowanie można w przypadku falowodów pominąć, dla linii koncentrycznej także, chyba, że w kablu koncentrycznym przewód zewnętrzny wykonany jest z plecionki metalowej. Jednakże w liniach planarnych nie może być pominięty, choć jest trudny do oszacowania.
| |
|
| |
|
| |
| *'''Porównanie strat'''
| |
|
| |
| Porównanie strat rozmaitych typów prowadnic falowych, zestawione na rys.3.9 prowadzi do przygnębiających wniosków: straty są duże.
| |
|
| |
|
| |
| {| border="1" cellpadding="5" cellspacing="0" align="center"
| |
| |-
| |
| !Rys.3.9. Tłumienie dla różnych typów
| |
| falowodów prostokątnych wykonanych
| |
|
| |
| z aluminium i srebra, oraz
| |
|
| |
| dla miedzianych kabli współosiowych,
| |
|
| |
| w funkcji częstotliwości.
| |
| ||[[Grafika:TTS_M3_Rys14.png]]
| |
| |-
| |
| |} | | |} |
|
| |
|
| |
| Można je pominąć w monolitycznych układach scalonych przy propagacji na odległość 1 mm, w układach hybrydowych przy propagacji na odległość 3 cm, w kablach współosiowych łączących aparaturę pomiarową pracującą w pasmie 1000 MHz na odległościach 1 metra. Ale w sieciach telewizji kablowej już nie można ich pominąć. Dodajmy, że w światłowodach kwarcowych straty są rzędu 0,2-0,4 dB/km. Aż trudno uwierzyć!
| |
|
| |
|
| <hr width="100%"> | | <hr width="100%"> |
|
| |
|
| = Pytania sprawdzające = | | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd36.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| (jeśli potrafisz na nie odpowiedzieć, to znaczy, że opanowałeś/aś materiał wykładu)
| | |} |
|
| |
|
| #Wymień i scharakteryzuj najważniejsze parametry prowadnicy falowej.
| | {| border="0" cellpadding="4" width="100%" |
| #Przypomnij sobie jakie mody mogą rozchodzić się w falowodach i scharakteryzuj je.
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd37.png|thumb|500px]] |
| #Co to jest dyspersja, w jakich warunkach i dlaczego dyspersja utrudnia transmisję sygnału.
| | |valign="top"| |
| #Przeanalizuj przyczyny powstawania strat przy transmisji mocy prowadnicami falowymi.
| |
| #Na czym polega efekt naskórkowości?
| |
| #Opisz kolejno prowadnice typu TEM.
| |
| #Narysuj konfigurację pól E i H dla modu podstawowego i naszkicuj kierunki przepływu prądów w ściankach falowodu prostokątnego.
| |
| #Dlaczego nie stosujemy falowodów prostokątnych, dla których stosunek a/b=1?
| |
| #W jakim pasmie częstotliwości może pracować falowód prostokątny?
| |
| #W jakim pasmie może pracować falowód cylindryczny?
| |
| #Jak uzasadnisz fakt, że obwodem zastępczym odcinka falowodu prostokątnego jest odcinek linii dwuprzewodowej?
| |
| #Jak zbudowana jest i jakie ma właściwości prowadnica mikropaskowa?
| |
| #Jak zbudowana jest i jakie ma właściwości linia koplanarna?
| |
| #Jakie są obszary zastosowań linii współosiowej, linii mikropaskowej i falowodu prostokątnego? Aby to uzasadnić porównaj parametry wymienionych typów prowadnic.
| |
| #Wymień argumenty przemawiające za rozwojem technologii i konstrukcji Mikrofalowych Monolitycznych Układów Scalonych na krzemie i arsenku galu.
| |
|
| |
|
| <hr width="100%">
| | |} |
| | |
| = Słownik =
| |
| | |
| *'''Częstotliwość graniczna''' - częstotliwość powyżej której może się propagować fala w falowodzie. Poniżej tej częstotliwości fala jest silnie tłumiona.
| |
| *'''Zestawienie typów fal:'''
| |
| **'''Fala typu TEM''' - wektory pola E i H leżą w płaszczyźnie prostopadłej do kierunku propagacji.
| |
| **'''Fala typu TE (zwana też H)''' - pole E posiada składowe tylko w płaszczyźnie prostopadłej do kierunku propagacji. Pole H posiada składowe w kierunku propagacji fali.
| |
| **'''Fala typu TM (zwana też E)''' - pole H posiada składowe tylko w płaszczyźnie prostopadłej do kierunku propagacji. Pole E posiada składowe w kierunku propagacji fali.
| |
| **'''Fala typu EH''' - zarówno pole E jak i pole H tej fali posiadają składowe w kierunku propagacji.
| |
| *'''Linie TEM:'''
| |
| **Linia współosiowa.
| |
| **Linia dwuprzewodowa.
| |
| **Symetryczna linia paskowa.
| |
| *'''Linie Quasi-TEM:'''
| |
| **Niesymetryczna linia paskowa:
| |
| **Linia koplanarna (falowód koplanarny).
| |
| **Linia koplanarna paskowa.
| |
| *'''Linie falowodowe:'''
| |
| **Falowód prostokątny. Mod podstawowy typu <math>TE_{10} (H10)\,</math>.
| |
| **Falowód kołowy (cylindryczny). Mod podstawowy typu <math>TE_{11} (H11)\,</math>.
| |
| *'''Mod (rodzaj) podstawowy''' dla danego falowodu - to mod fali o najmniejszej częstotliwości granicznej.
| |
|
| |
|
| <hr width="100%"> | | <hr width="100%"> |
|
| |
|
| = Bibliografia = | | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd38.png|thumb|500px]] |
| | |valign="top"| |
|
| |
|
| #Bogdan Galwas. Miernictwo mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1985, Rozdział 1, 2 i 3.
| | |} |
| #Tadeusz Morawski, Wojciech Gwarek. Pola i fale elektromagnetyczne, Wydawnictwa Naukowo-Techniczne, Warszawa, 1998, Rozdział 1 do 8.
| |
| #Janusz Dobrowolski. Technika wielkich częstotliwości, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa, 1998 Rozdział 1 i 3.
| |
| #Stanisław Rosłoniec. Liniowe obwody mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1999, Rozdział 2.
| |
| | |
| <hr width="100%">
| |