GKIW Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 89: | Linia 89: | ||
Niech położenie punktu o współrzędnych <math>(x_p, y_p)</math> na płaszczyźnie reprezentuje wektor P : | Niech położenie punktu o współrzędnych <math>(x_p, y_p)</math> na płaszczyźnie reprezentuje wektor P : | ||
:<math>P=\begin{bmatrix} | :<math>P=\begin{bmatrix} x_P \\y_P \\ 1 \end{bmatrix}</math> | ||
Jeśli macierz M opisuje pewną transformację geometryczną to operację tę można opisać następująco: | Jeśli macierz M opisuje pewną transformację geometryczną to operację tę można opisać następująco: | ||
| Linia 97: | Linia 97: | ||
czyli: | czyli: | ||
:<math>\begin{bmatrix} | :<math>\begin{bmatrix} x_P^{'} \\y_P^{'} \\ 1 \end{bmatrix}=M\cdot \begin{bmatrix} x_P \\y_P \\ 1 \end{bmatrix}</math> | ||
gdzie P' opisuje położenie punktu po przekształceniu. Oczywiście, jeśli wynik mnożenia macierzy jest nieznormalizowany, to należy dokonać normalizacji. | gdzie P' opisuje położenie punktu po przekształceniu. Oczywiście, jeśli wynik mnożenia macierzy jest nieznormalizowany, to należy dokonać normalizacji. | ||
| Linia 105: | Linia 105: | ||
Można powiedzieć, że macierz M definiuje liniowe funkcje określające każdą ze współrzędnych punktu tzn.: | Można powiedzieć, że macierz M definiuje liniowe funkcje określające każdą ze współrzędnych punktu tzn.: | ||
:<math>\begin{cases} x_P^{'}=f_{XM}(x_P, y_P, z_P) \\ y_P^{'}=f_{YM}(x_P, y_P, z_P) \end{cases}</math> | |||
Wykorzystując rachunek macierzowy przekształcenia punktu można opisać również za pomocą prawostronnego mnożenia macierzy. Wtedy, dla przyjętych wyżej danych operacja wyglądałaby tak.: | |||
:<math>{P'}^T=P^T\cdot M^T</math> | |||
Jak widać tę samą operację można zapisać jako mnożenie lewostronne lub prawostronne przez macierz przekształcenia. | |||
Tak naprawdę trudno byłoby wskazać uzasadnienie dla wyboru jednej lub drugiej formy zapisu. W książkach dotyczących grafiki komputerowej w ostatnich latach częściej stosowany jest zapis lewostronnego mnożenia, chociaż są autorzy, którzy nadal konsekwentnie trzymają się mnożenia prawostronnego. Natomiast sposób używania zależy od przyzwyczajeń i upodobań użytkownika. Jedno jest jednak bardzo istotne – konsekwencja. Nie można mieszać postaci opisu. | |||
|} | |} | ||
| Linia 112: | Linia 120: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_6.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_6.png|400px]] | ||
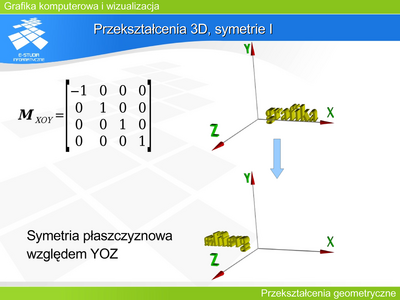
|valign="top"| | |valign="top"|'''Przekształcenie 2D, symetrie I''' | ||
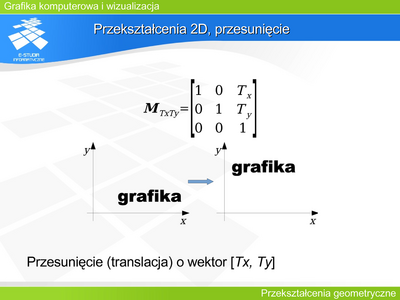
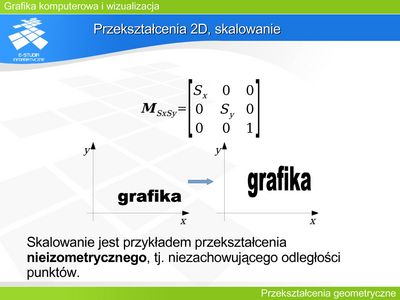
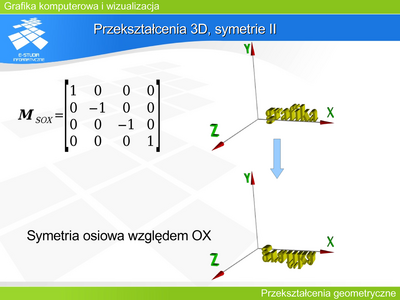
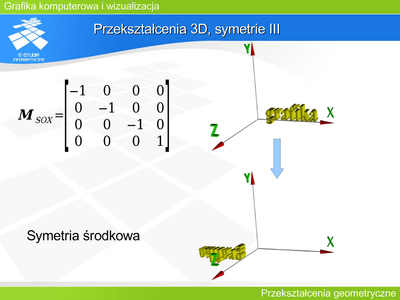
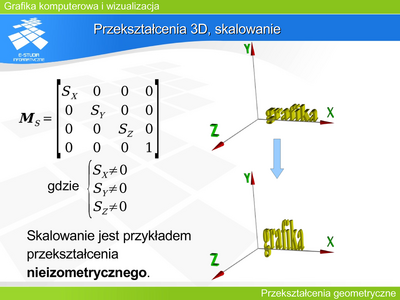
Można zaproponować pewien minimalny zestaw operacji: symetrie (względem osi układu współrzędnych i środkowa), obroty, przesunięcie (translacja), skalowanie oraz pochylenie. | |||
|} | |} | ||
| Linia 118: | Linia 128: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_7.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_7.png|400px]] | ||
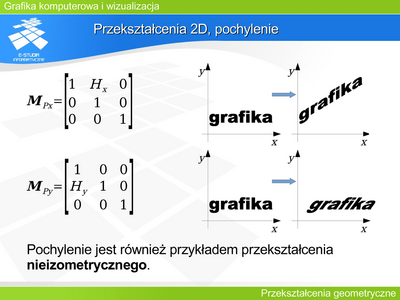
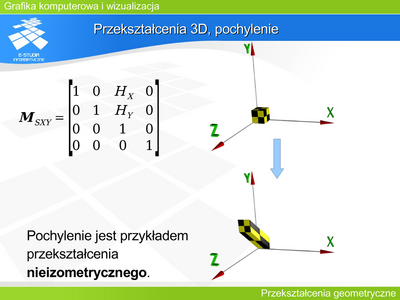
|valign="top"| | |valign="top"|'''Przekształcenie 2D, pochylenie''' | ||
Pochylenie jest rzadziej stosowanym przekształceniem. Daje możliwość zniekształcenia figury. Nie zachowuje odległości punktów. Figura i jej obraz w tym przekształceniu nie są podobne. | |||
|} | |} | ||
| Linia 124: | Linia 138: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_8.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_8.png|400px]] | ||
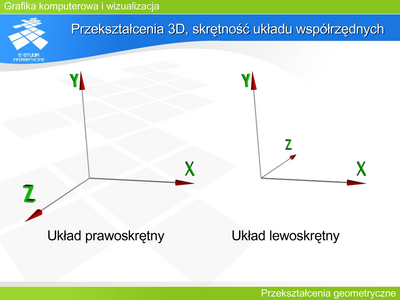
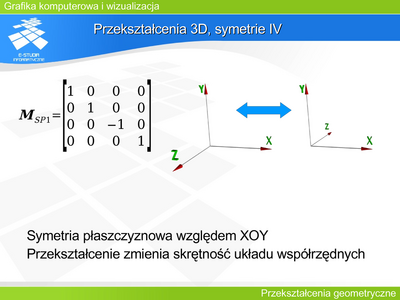
|valign="top"| | |valign="top"|'''Przekształcenie 3D, skrętność układu współrzędnych''' | ||
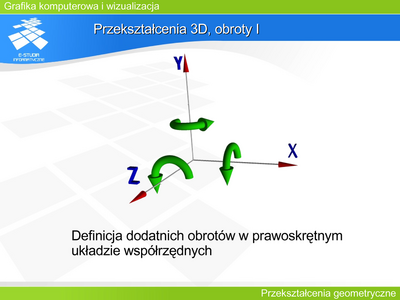
Możliwe są dwa ustawienia osi trójwymiarowego układu współrzędnych. Najczęściej do opisu położenia obiektów na scenie (w przestrzeni obiektu) stosowany jest układ prawoskrętny. Natomiast w operacjach związanych z rzutowaniem układ lewoskrętny. Wybór układu współrzędnych dla operacji rzutowania jest konsekwencją naturalnego rozumienia odległości obiektu od obserwatora. Jeśli osie OX i OY zdefiniują układ współrzędnych na rzutni (utożsamianej z płaszczyzną XOY) (pozioma oś OX skierowana w prawo i pionowa oś OY skierowana do góry), to kierunek wzrostu odległości od obserwatora wskaże oś OZ. Tak zdefiniowany układ współrzędnych będzie układem lewoskrętnym. | |||
Niech położenie punktu o współrzędnych <math>(x_p, y_p, z_p)</math> w przestrzeni trójwymiarowej reprezentuje wektor P : | |||
|} | |} | ||
Wersja z 11:57, 5 gru 2006

|

|
|
|
|
|

|
|
|
|
|
|

|
|
|
|
|
|
|

|
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|