|
|
| Linia 70: |
Linia 70: |
| |valign="top"|'''Współrzędne jednorodne znormalizowane''' | | |valign="top"|'''Współrzędne jednorodne znormalizowane''' |
|
| |
|
| Niech <math>x_p, y_p, z_p\,</math>, opisują położenie punktu w trójwymiarowym kartezjańskim układzie współrzędnych. W grafice komputerowej do opisu położenia oraz opisu operacji (transformacji geometrycznych), którym punkty będą podlegały, jest używany '''układ współrzędnych jednorodnych znormalizowanych'''. Dzięki temu wszystkie stosowane transformacje geometryczne mogą być opisane w identyczny sposób za pomocą mnożenia macierzowego. Jeśli współrzędne <math>x_p, y_p, z_p\,</math> opisują położenie punktu, to odpowiada temu wektor <math>P=\begin{bmatrix} x_p & y_p & z_p & 1 \\ \end{bmatrix}^T</math> we współrzędnych jednorodnych znormalizowanych. We współrzędnych nieznormalizowanych wektor ten miałby postać <math>P=\begin{bmatrix} x_p & y_p & z_p & 1 \\ \end{bmatrix}^T</math> dla . Przy czym , , , co nosi nazwę operacji normalizacji. | | Niech <math>x_p, y_p, z_p\,</math>, opisują położenie punktu w trójwymiarowym kartezjańskim układzie współrzędnych. W grafice komputerowej do opisu położenia oraz opisu operacji (transformacji geometrycznych), którym punkty będą podlegały, jest używany '''układ współrzędnych jednorodnych znormalizowanych'''. Dzięki temu wszystkie stosowane transformacje geometryczne mogą być opisane w identyczny sposób za pomocą mnożenia macierzowego. Jeśli współrzędne <math>x_p, y_p, z_p\,</math> opisują położenie punktu, to odpowiada temu wektor <math>P=\begin{bmatrix} x_p & y_p & z_p & 1 \\ \end{bmatrix}^T</math> we współrzędnych jednorodnych znormalizowanych. We współrzędnych nieznormalizowanych wektor ten miałby postać <math>P=\begin{bmatrix} \overset{\sim}{x_p} & \overset{\sim}{y_p} & \overset{\sim}{z_p} & \overset{\sim}{N} \\ \end{bmatrix}^T</math> dla <math>\overset{\sim}{N}\neq 0</math> . Przy czym <math>\displaystyle x_p=\frac{\overset{\sim}{x_p}}{\overset{\sim}{N}}</math> , <math>\displaystyle y_p=\frac{\overset{\sim}{y_p}}{\overset{\sim}{N}}</math> , <math>\displaystyle z_p=\frac{\overset{\sim}{z_p}}{\overset{\sim}{N}}</math> , co nosi nazwę operacji normalizacji. |
| | |
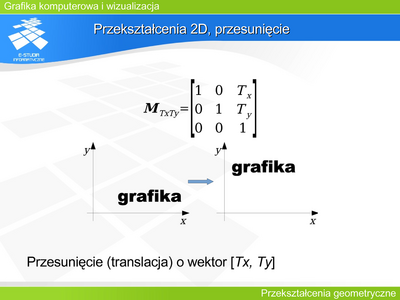
| | Zastosowanie w przypadku przesunięcia na płaszczyźnie współrzędnych jednorodnych można sobie wyobrazić jako umieszczenie płaszczyzny, na której pracujemy, w trójwymiarowym układzie współrzędnych, w taki sposób, aby nie przechodziła ona przez początek układu (tzn. dla <math>z=h_z\neq 0</math> ). Wtedy analogiczne opisanie operacji translacji na płaszczyźnie (ale już jako macierz 3x3) da poprawne rozwiązanie, gdyż punkt stały – początek układu współrzędnych jest poza płaszczyzną, na której jest wykonywana operacja. Jednocześnie, aby wynik operacji znajdował się na tej samej płaszczyźnie, najprościej operować na współrzędnych znormalizowanych, czyli pracować na płaszczyźnie <math>z=1</math>. |
| | |
| | Gdyby operacja normalizacji nie została wykonana mogłoby się zdarzyć, że wynik operacji leżałby na innej płaszczyźnie – a to nie miałoby sensu |
| | |
| | A zatem zawsze jeśli wynik operacji będzie nieznormalizowany zostanie przeprowadzona operacja normalizacji. |
| | |
| | Analogicznie dla przekształceń trójwymiarowych można wyobrazić sobie umieszczenie przestrzeni 3D i trójwymiarowego układu współrzędnych wewnątrz układu czterowymiarowego, tak aby nie zawierał on początku układu współrzędnych.. |
| | |
| |} | | |} |
|
| |
|
| Linia 76: |
Linia 85: |
| {| border="0" cellpadding="5" width="100%" | | {| border="0" cellpadding="5" width="100%" |
| |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_5.png|400px]] | | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_5.png|400px]] |
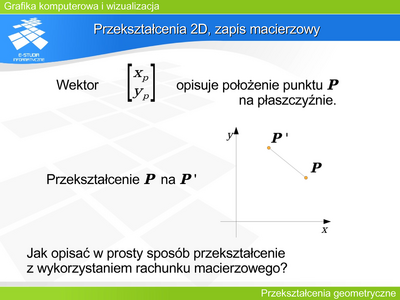
| |valign="top"| | | |valign="top"|'''Przekształcenia 2D''' |
| | |
| | Niech położenie punktu o współrzędnych <math>(x_p, y_p)</math> na płaszczyźnie reprezentuje wektor P : |
| | |
| | :<math>P=\begin{bmatrix} x_p \\y_p \\ 1 \end{bmatrix}</math> |
| | |
| | Jeśli macierz M opisuje pewną transformację geometryczną to operację tę można opisać następująco: |
| | |
| | :<math>P'=M\cdot P</math> |
| | |
| | czyli: |
| | |
| | :<math>\begin{bmatrix} x_p^{'} \\y_p^{'} \\ 1 \end{bmatrix}=M\cdot \begin{bmatrix} x_p \\y_p \\ 1 \end{bmatrix}</math> |
| | |
| | gdzie P' opisuje położenie punktu po przekształceniu. Oczywiście, jeśli wynik mnożenia macierzy jest nieznormalizowany, to należy dokonać normalizacji. |
| | |
| | W grafice komputerowej operacje na płaszczyźnie opisuje macierz 3x3. |
| | |
| | Można powiedzieć, że macierz M definiuje liniowe funkcje określające każdą ze współrzędnych punktu tzn.: |
| | |
| | |
| | |
| |} | | |} |
|
| |
|