|
|
| Linia 68: |
Linia 68: |
| {| border="0" cellpadding="5" width="100%" | | {| border="0" cellpadding="5" width="100%" |
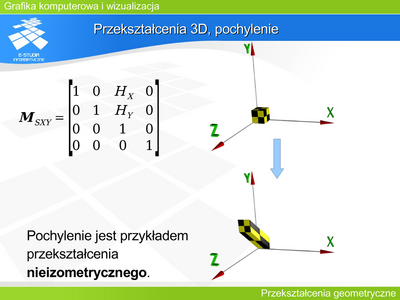
| |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_4.png|400px]] | | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_4.png|400px]] |
| |valign="top"| | | |valign="top"|'''Współrzędne jednorodne znormalizowane''' |
| | |
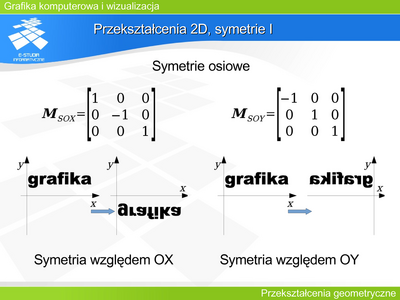
| | Niech <math>x_p, y_p, z_p\,</math>, opisują położenie punktu w trójwymiarowym kartezjańskim układzie współrzędnych. W grafice komputerowej do opisu położenia oraz opisu operacji (transformacji geometrycznych), którym punkty będą podlegały, jest używany '''układ współrzędnych jednorodnych znormalizowanych'''. Dzięki temu wszystkie stosowane transformacje geometryczne mogą być opisane w identyczny sposób za pomocą mnożenia macierzowego. Jeśli współrzędne <math>x_p, y_p, z_p\,</math> opisują położenie punktu, to odpowiada temu wektor <math>P=\begin{bmatrix} x_p & y_p & z_p & 1 \\ \end{bmatrix}^T</math> we współrzędnych jednorodnych znormalizowanych. We współrzędnych nieznormalizowanych wektor ten miałby postać <math>P=\begin{bmatrix} x_p & y_p & z_p & 1 \\ \end{bmatrix}^T</math> dla . Przy czym , , , co nosi nazwę operacji normalizacji. |
| |} | | |} |
|
| |
|