|
|
| Linia 19: |
Linia 19: |
| Współczesna grafika komputerowa operuje na milionach elementów (punktów, trójkątów). Przy tak dużej liczbie zachodzi konieczność opisania operacji geometrycznych w taki sposób, aby ich wykonanie było z jednej strony efektywne, a z drugiej, aby opis był prosty i ujednolicony. Takie warunki spełnia opis macierzowy. | | Współczesna grafika komputerowa operuje na milionach elementów (punktów, trójkątów). Przy tak dużej liczbie zachodzi konieczność opisania operacji geometrycznych w taki sposób, aby ich wykonanie było z jednej strony efektywne, a z drugiej, aby opis był prosty i ujednolicony. Takie warunki spełnia opis macierzowy. |
|
| |
|
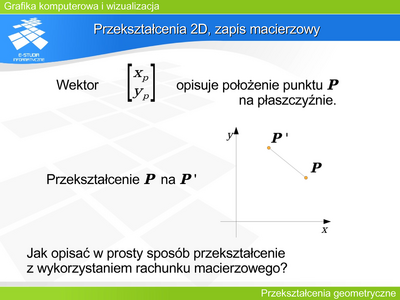
| Niech <math>P=\begin{bmatrix} x_P & y_P \\ \end{bmatrix}^T</math> opisuje położenie punktu na płaszczyźnie. Najprostszym rozwiązaniem byłoby przyjęcie, że macierz <math>M(2\times 2)</math> opisuje przekształcenie punktu <math>P\,</math> na <math>P'\,</math> i że <math>P'=M\cdot P</math> | | Niech <math>P=\begin{bmatrix} x_p & y_p \\ \end{bmatrix}^T</math> opisuje położenie punktu na płaszczyźnie. Najprostszym rozwiązaniem byłoby przyjęcie, że macierz <math>M(2\times 2)</math> opisuje przekształcenie punktu <math>P\,</math> na <math>P'\,</math> i że <math>P'=M\cdot P</math> |
| |} | | |} |
|
| |
|
| Linia 45: |
Linia 45: |
| Niech <math>M_{T1}=\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}</math>. Niech wektor <math>P=\begin{bmatrix} T_X & T_Y \\ \end{bmatrix}</math> opisuje translację punktu na płaszczyźnie. | | Niech <math>M_{T1}=\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}</math>. Niech wektor <math>P=\begin{bmatrix} T_X & T_Y \\ \end{bmatrix}</math> opisuje translację punktu na płaszczyźnie. |
|
| |
|
| Czy można znaleźć takie a, b, c, d, aby <math>M_{T1}=\begin{bmatrix} x_P+T_X \\ y_P+T_Y \\ \end{bmatrix}=\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}\cdot \begin{bmatrix} x_P \\ y_P \\ \end{bmatrix}</math> dla <math>T_X\neq 0</math> i <math>T_Y\neq 0</math> . | | Czy można znaleźć takie a, b, c, d, aby <math>M_{T1}=\begin{bmatrix} x_p+T_X \\ y_p+T_Y \\ \end{bmatrix}=\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}\cdot \begin{bmatrix} x_p \\ y_p \\ \end{bmatrix}</math> dla <math>T_X\neq 0</math> i <math>T_Y\neq 0</math> . |
| | |
| | Widać że nie jest to możliwe dla współrzędnych dowolnego punktu. Na dodatek punkt <math>P=\begin{bmatrix} 0 & 0 \\ \end{bmatrix}^T</math> byłby punktem stałym takiego przekształcenia. |
| | |
| | Jak zatem opisać translację na płaszczyźnie? |
| | |
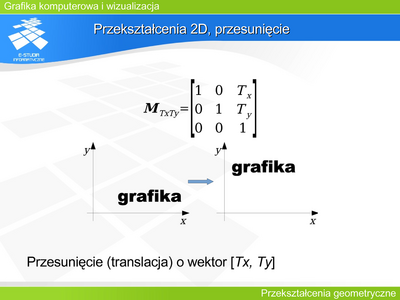
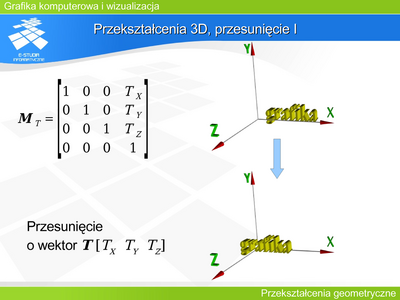
| | Operację tę można opisać macierzą <math>M=\begin{bmatrix} 1 & 0 & T_X \\ 0 & 1 & T_Y\\ 0 & 0 & 1 \end{bmatrix}</math> |
| | |
| | Między współrzędnymi zachodzi następujący związek: |
| | |
| | :<math>M=\begin{bmatrix} X_p^{'} \\ Y_p^{'}\\ 1 \end{bmatrix}=\begin{bmatrix} 1 & 0 & T_X \\ 0 & 1 & T_Y\\ 0 & 0 & 1 \end{bmatrix}\cdot \begin{bmatrix} X_p \\ Y_p\\ 1 \end{bmatrix}</math> |
| | |
| | i jest to równoważne opisowi translacji o wektor w postaci układu równań: |
| | |
| | :<math>\begin{cases} x_p^{'}=x_p+T_X \\ y_p^{'}=y_p+T_Y \end{cases}</math> |
| | |
| | Tak wykonana operacja wymaga użycia współrzędnych jednorodnych. |
| | |
| |} | | |} |
|
| |
|