|
|
| Linia 15: |
Linia 15: |
| {| border="0" cellpadding="5" width="100%" | | {| border="0" cellpadding="5" width="100%" |
| |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_1.png|400px]] | | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_1.png|400px]] |
| |valign="top"| | | |valign="top"|'''Przekształcenia 2D, zapis macierzowy''' |
| | |
| | Współczesna grafika komputerowa operuje na milionach elementów (punktów, trójkątów). Przy tak dużej liczbie zachodzi konieczność opisania operacji geometrycznych w taki sposób, aby ich wykonanie było z jednej strony efektywne, a z drugiej, aby opis był prosty i ujednolicony. Takie warunki spełnia opis macierzowy. |
| | |
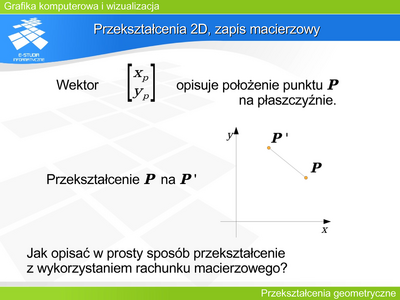
| | Niech <math>P=\begin{bmatrix} x_P & y_P \\ \end{bmatrix}^T</math> opisuje położenie punktu na płaszczyźnie. Najprostszym rozwiązaniem byłoby przyjęcie, że macierz <math>M(2\times 2)</math> opisuje przekształcenie punktu <math>P\,</math> na <math>P'\,</math> i że <math>P'=M\cdot P</math> |
| |} | | |} |
|
| |
|
| Linia 22: |
Linia 26: |
| {| border="0" cellpadding="5" width="100%" | | {| border="0" cellpadding="5" width="100%" |
| |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_2.png|400px]] | | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_2.png|400px]] |
| |valign="top"| | | |valign="top"|'''Przekształcenia 2D, obrót, problem przesunięcia I''' |
| | |
| | Można zastanowić się nad tym, czy takie podejście do problemu wystarczy do opisu prostych operacji geometrycznych. |
| | |
| | Rozpatrzmy zestaw przekształceń na płaszczyźnie: obrót, skalowanie, przesunięcie (translację). |
| | |
| | Można zaproponować macierz 2x2, która, opisuje obrót punktu wokół początku układu współrzędnych. |
| | |
| | Analogiczny opis można zaproponować dla operacji skalowania. |
| |} | | |} |
|
| |
|
| Linia 29: |
Linia 41: |
| {| border="0" cellpadding="5" width="100%" | | {| border="0" cellpadding="5" width="100%" |
| |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_3.png|400px]] | | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_3.png|400px]] |
| |valign="top"| | | |valign="top"|'''Przekształcenia 2D, obrót, problem przesunięcia II''' |
| | |
| | Niech <math>M_{T1}=\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}</math>. Niech wektor <math>P=\begin{bmatrix} T_X & T_Y \\ \end{bmatrix}</math> opisuje translację punktu na płaszczyźnie. |
| | |
| | Czy można znaleźć takie a, b, c, d, aby <math>M_{T1}=\begin{bmatrix} x_P+T_X \\ y_P+T_Y \\ \end{bmatrix}=\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}\cdot \begin{bmatrix} x_P \\ y_P \\ \end{bmatrix}</math> dla <math>T_X\neq 0</math> i <math>T_Y\neq 0</math> . |
| |} | | |} |
|
| |
|