GKIW Moduł 7: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 276: | Linia 276: | ||
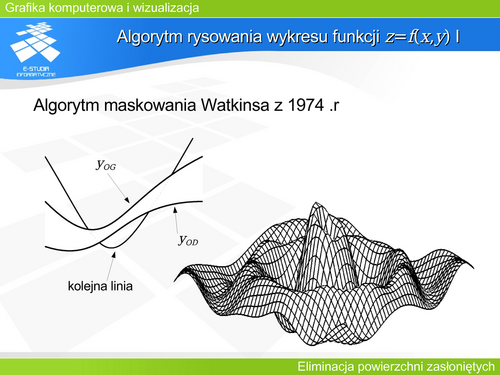
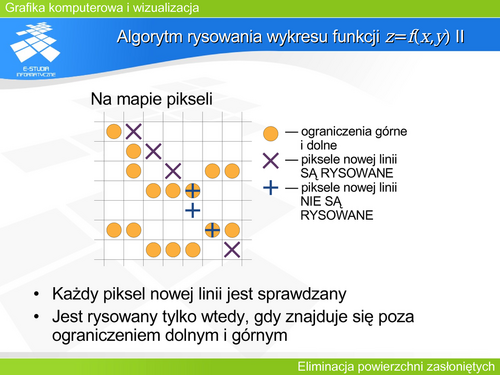
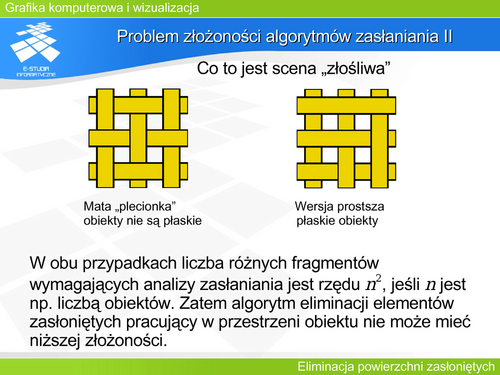
Można pokazać, że dla wybranych scen minimalna złożoność algorytmów pracujących w przestrzeni obiektu musi być rzędu kwadratowego. Wynika to z budowy sceny. Wyrafinowane algorytmy mogą w tym przypadku dać rozwiązanie gorsze niż kwadratowe. | Można pokazać, że dla wybranych scen minimalna złożoność algorytmów pracujących w przestrzeni obiektu musi być rzędu kwadratowego. Wynika to z budowy sceny. Wyrafinowane algorytmy mogą w tym przypadku dać rozwiązanie gorsze niż kwadratowe. | ||
|} | |} | ||
---- | ---- | ||
| Linia 355: | Linia 349: | ||
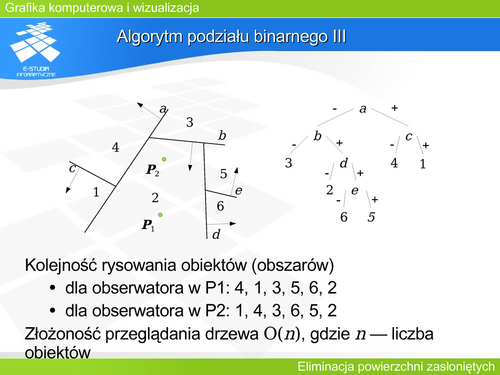
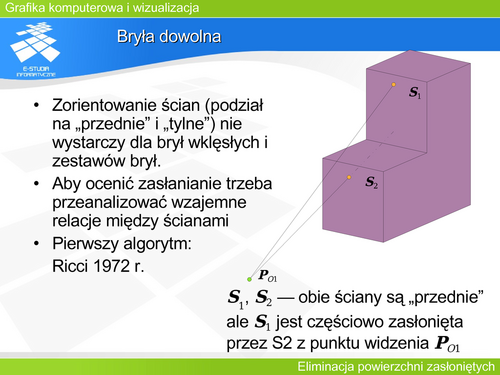
Pierwszy algorytm rozstrzygania widoczności dla dowolnych brył, przy założeniu że ściany są trójkątami (a przecież dowolny wielokąt zawsze może zostać rozłożony na zbiór trójkątów) podał Ricci w 1972 roku. Był to algorytm pracujący metodą „każdy z każdym” o kwadratowej złożoności obliczeniowej. | Pierwszy algorytm rozstrzygania widoczności dla dowolnych brył, przy założeniu że ściany są trójkątami (a przecież dowolny wielokąt zawsze może zostać rozłożony na zbiór trójkątów) podał Ricci w 1972 roku. Był to algorytm pracujący metodą „każdy z każdym” o kwadratowej złożoności obliczeniowej. | ||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M7_Slajd24.png|thumb|500px]] | |||
|valign="top"| | |||
|} | |} | ||
---- | ---- | ||
Wersja z 10:40, 4 gru 2006
 |
 |
 |
 |
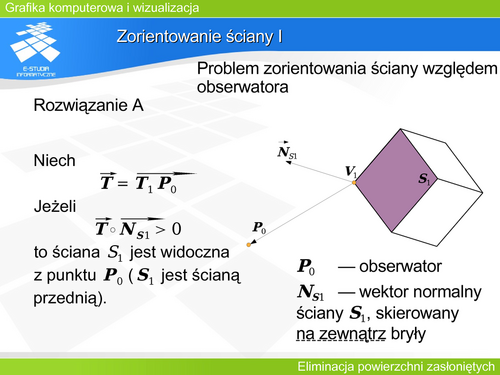
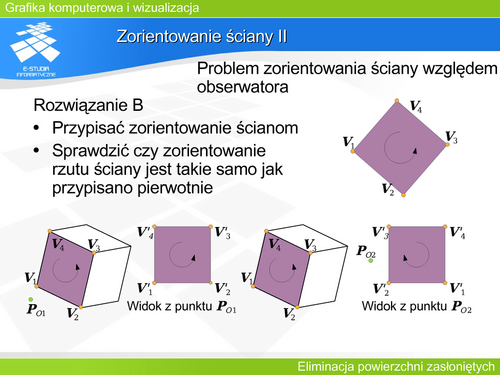
Bryła wypukła I Zadanie określenia widoczności elementów wielościanu wypukłego można więc rozwiązać na dwa sposoby korzystając z rozwiązań A i B sprawdzających zorientowanie poszczególnych ścian. |
 |