GKIW Moduł 6a: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 65: | Linia 65: | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
oraz | |||
<math>P=\begin{bmatrix} | |||
x&y&z&1 \\ | |||
\end{bmatrix}</math> | |||
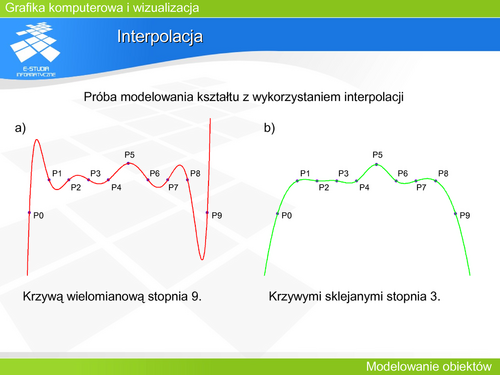
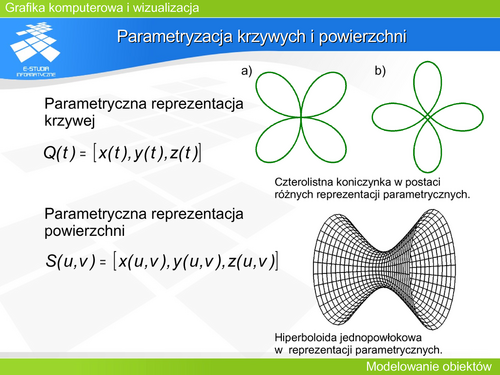
Przy czym dla każdej powierzchni drugiego stopnia jest znana reprezentacja parametryczna. Dla przykładowej hiperboloidy jednopowłokowej z prezentowanego rysunku: | |||
Zalety stosowania powierzchni drugiego stopnia: | |||
Możliwość łatwego wyznaczenia wektora normalnego | |||
<math>\cec N= [\frac{\delta f}{\delta x} \frac{\delta f}{\delta y} \frac{\delta f}{\delta z}]</math> | |||
Możliwość szybkiego wyznaczenia przecięcia powierzchni z prostą – efektywność stosowania w algorytmach związanych z metodą śledzenia promieni. | |||
Możliwość szybkiego wyznaczenia z na podstawie x i y – przydatne w algorytmach eliminacji elementów zasłoniętych. | |||
|} | |} | ||
| Linia 74: | Linia 87: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GK_M6n_Slajd5.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GK_M6n_Slajd5.png|thumb|500px]] | ||
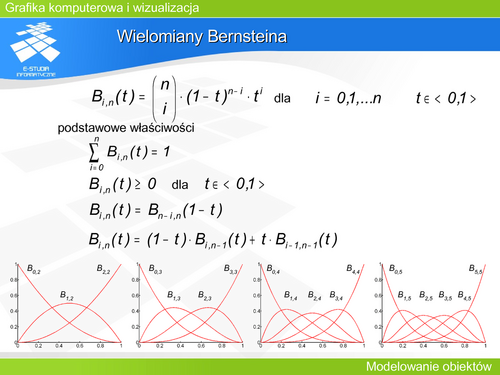
|valign="top"| | |valign="top"|Wielomiany Bernsteina są funkcjami bazowymi dla krzywych Béziera. Ich właściwości mają decydujący wpływ na właściwości krzywych. | ||
Rysunek przedstawia wykresy wielomianów Bernsteina 2, 3, 4 i 5 stopnia. Najczęściej mamy do czynienia z wielomianami stopnia 3. W tym przypadku: | |||
<math>B_{0,3}(t)=(1-t)^3, B_{1,3}(t)=3t(1-t)^2, B_{2,3}(t)=3t^2(1-t), B_{3,3}(t)=t^3</math> | |||
Ostatnia właściwość (zależność rekurencyjna) prowadzi do algorytmu wyznaczania punktów na krzywej bazującej na wielomianach Bernsteina. | |||
|} | |} | ||
---- | ---- | ||
| Linia 80: | Linia 99: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GK_M6n_Slajd6.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GK_M6n_Slajd6.png|thumb|500px]] | ||
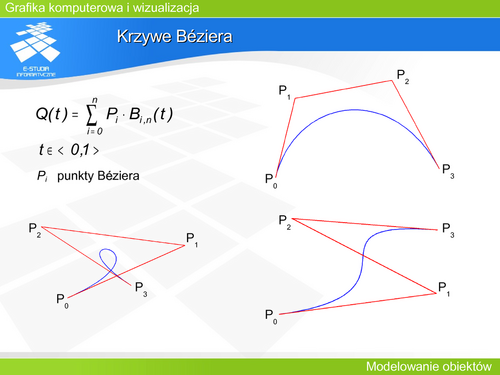
|valign="top"| | |valign="top"|Krzywa Béziera zawdzięcza swą nazwę Pierre’owi Bézierowi, warto jednak pamiętać, | ||
że rozwiązanie to miało dwóch niezależnych twórców. Drugim był P. de Casteljau. Jego nazwiskiem został opatrzony podstawowy algorytm wyznaczania punktu krzywej. | |||
Krzywa Béziera stopnia n jest definiowana przez n+1 punktów <math>P_0, P_1, P_2,…P_n</math> w bazie wielomianów Bernsteina. Jest to krzywa gładka, której kształt zależy od położenia punktów kontrolnych. Najczęściej stosowane są krzywe stopnia 3. | |||
Użytkownicy komputerów spotykają się z nią na co dzień w postaci fontów, których kształt jest projektowany właśnie z jej wykorzystaniem | |||
|} | |} | ||
---- | ---- | ||
| Linia 86: | Linia 109: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GK_M6n_Slajd7.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GK_M6n_Slajd7.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Krzywa Béziera interpoluje dwa końcowe punkty kontrolne i aproksymuje pozostałe. Oznacza to, że dla krzywej stopnia 3 , jeśli ustalone są punkty końcowe (a tak jest najczęściej), to dwa pozostałe punkty decydują o kształcie. | ||
Wady: | |||
- Brak możliwości reprezentacji krzywych stożkowych. | |||
- Zmiana reprezentacji krzywej po rzutowaniu perspektywicznym. | |||
|} | |} | ||
---- | ---- | ||
| Linia 92: | Linia 120: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GK_M6n_Slajd8.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GK_M6n_Slajd8.png|thumb|500px]] | ||
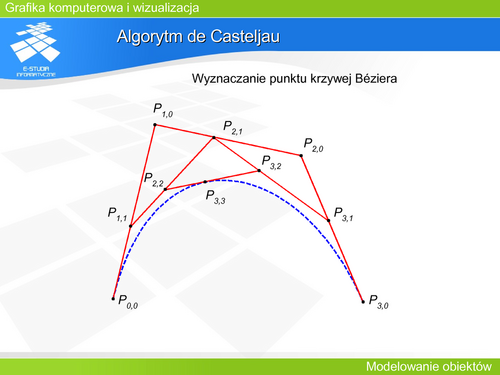
|valign="top"| | |valign="top"|Korzystając z właściwości rekurencyjnej wielomianów Bernsteina można wyznaczyć punkty krzywej Béziera. | ||
Algorytm de Casteljau | |||
wyznaczania punktu leżącego na krzywej Béziera na podstawie ciągu punktów kontrolnych <math>P_0, P_1, P_2,…P_n</math | |||
for i:= 0 to n do Pi,0 = Pi; | |||
for j:=1 to n do | |||
for i:=j to n do | |||
Pi,j := (1-t)*Pi-1,j-1 + t*Pi,j-1; | |||
Jeśli zadaniem jest wyznaczenie dużej liczby punktów leżących na krzywej Béziera to tańszym obliczeniowo rozwiązaniem będzie przejście w wielomianach Bernsteina do postaci naturalnej wielomianu i obliczanie jego wartości algorytmem Hornera. | |||
|} | |} | ||
---- | ---- | ||
| Linia 250: | Linia 287: | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
---- | ----</math> | ||