GKIW Moduł 6a: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 19: | Linia 19: | ||
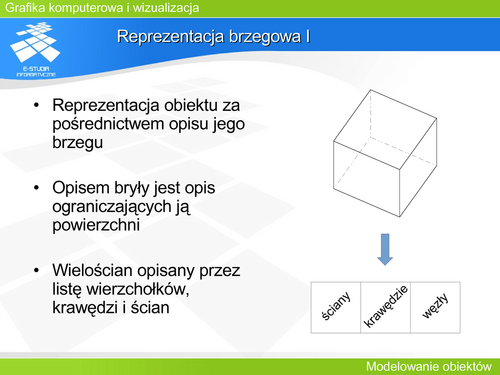
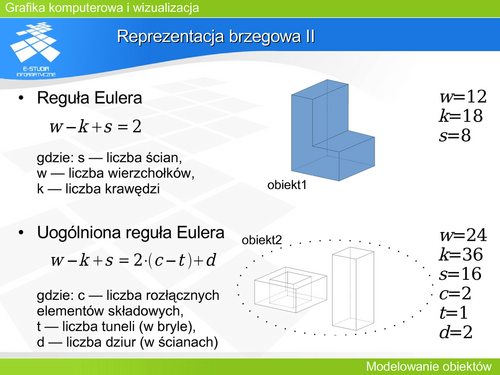
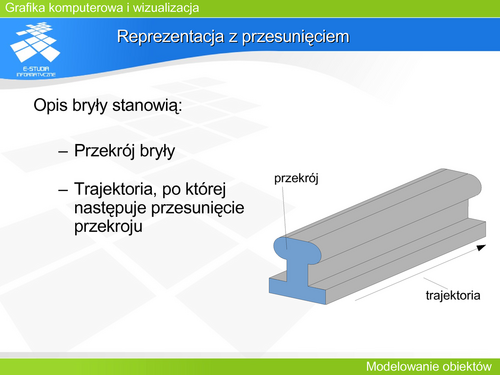
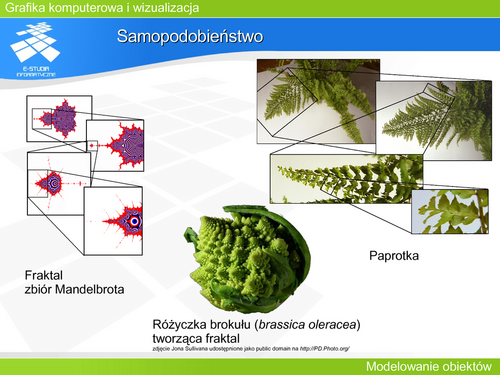
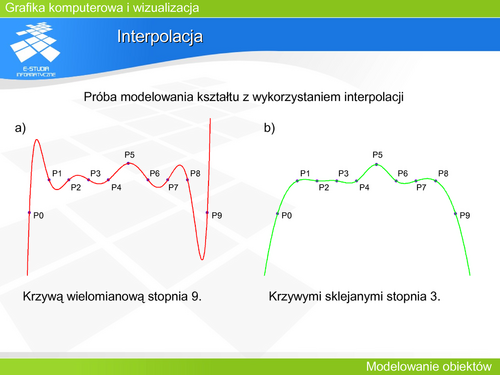
Jeżeli dany jest ciąg parami różnych liczb <math>t_0, t_1, t_2, …t_n </math>– węzłów interpolacyjnych i odpowiadających im punktom <math>P_0, P_1, P_2,…P_n.</math> To poszukujemy krzywej wielomianowej P(t) takiej, że jest ona stopnia co najwyżej n oraz P(ti)=Pi dla każdego i. Tak sformułowane zadanie jest zadaniem interpolacyjnym Lagrange’a i ma dokładnie jedno rozwiązanie w postaci: | Jeżeli dany jest ciąg parami różnych liczb <math>t_0, t_1, t_2, …t_n </math>– węzłów interpolacyjnych i odpowiadających im punktom <math>P_0, P_1, P_2,…P_n.</math> To poszukujemy krzywej wielomianowej P(t) takiej, że jest ona stopnia co najwyżej n oraz P(ti)=Pi dla każdego i. Tak sformułowane zadanie jest zadaniem interpolacyjnym Lagrange’a i ma dokładnie jedno rozwiązanie w postaci: | ||
<math>P(t)=\Sigma_{ | <math>P(t)=\Sigma_{i=0 }^n P_i( \prod_{j=0j\ne i}^n \frac{t-t_j}{t_i-t_j})</math> | ||
Wersja z 11:37, 17 lis 2006
 |
Komputerowe wspomaganie projektowania jest dziedziną stosunkowo nową, ale szeroko wykorzystywaną przez różnych specjalistów. Różnorakie zastosowania wymagają definicji – opisu reprezentacji różnych obiektów. Z jednej strony typowe obiekty mechaniczne czy architektoniczne, z drugiej efekty specjalne filmów science fiction, gdzie jedynym ograniczeniem jest wyobraźnia twórców. Z drugiej strony systemy wspomagania projektowania dają dodatkowe możliwości wykonywania wielu obliczeń związanych bezpośrednio z dziedziną zastosowania – obliczeń konstrukcyjnych czy wytrzymałościowych. Oczywiście grafika komputerowa daje możliwość zobaczenia projektu – możliwość wizualizacji wyobrażeń projektanta. Niezbędne staje się narzędzie do modelowania kształtu – obiektu, powierzchni. Warto zwrócić uwagę na fakt, że użytkownicy takich systemów reprezentują różne poziomy przygotowania informatycznego. System modelowania powinien być więc prosty i efektywny, powinien dawać możliwość definicji kształtu za pomocą minimalnej liczby parametrów, a modyfikacja kształtu powinna dotyczyć wybranego fragmentu, a nie całości krzywej czy powierzchni. |
 |
W latach sześćdziesiątych XX wieku w fabryce Renault rozpoczął pracę pierwszy system modelowania geometrycznego na użytek komputerowego wspomagania projektowania. Twórcą tego systemu był P. Bézier – będący jedną z najważniejszych postaci w tej dziedzinie. Dzisiaj każda fabryka samochodów projektuje kształty karoserii wykorzystując modelowanie geometryczne.
Istnieje wiele metod modelowania krzywych i powierzchni. Mają one różne właściwości i wymagają osobnego omówienia. |
 |
Wydawać by się mogło, że najprostszą forma modelowania krzywej jest wskazanie zbioru punktów na niej leżących a następnie połączenie ich krzywą interpolującą – najprościej wielomianową. Jeżeli dany jest ciąg parami różnych liczb Parser nie mógł rozpoznać (błąd składni): {\displaystyle t_0, t_1, t_2, …t_n } – węzłów interpolacyjnych i odpowiadających im punktom Parser nie mógł rozpoznać (błąd składni): {\displaystyle P_0, P_1, P_2,…P_n.} To poszukujemy krzywej wielomianowej P(t) takiej, że jest ona stopnia co najwyżej n oraz P(ti)=Pi dla każdego i. Tak sformułowane zadanie jest zadaniem interpolacyjnym Lagrange’a i ma dokładnie jedno rozwiązanie w postaci:
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
