GKIW Moduł 6a: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GK_M6n_Slajd1.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GK_M6n_Slajd1.png|thumb|500px]] | ||
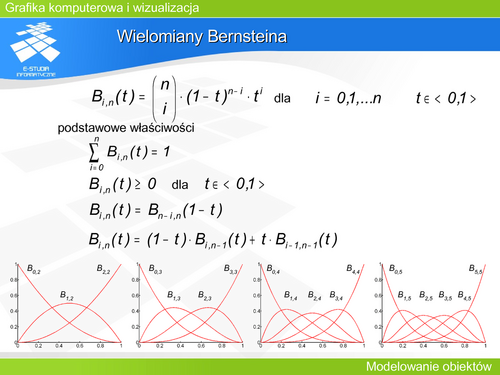
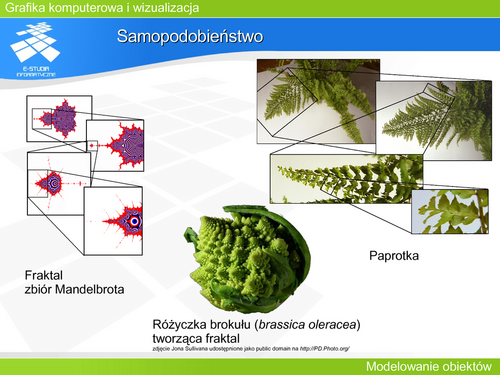
|valign="top"| | |valign="top"|Komputerowe wspomaganie projektowania jest dziedziną stosunkowo nową, ale szeroko wykorzystywaną przez różnych specjalistów. Różnorakie zastosowania wymagają definicji – opisu reprezentacji różnych obiektów. Z jednej strony typowe obiekty mechaniczne czy architektoniczne, z drugiej efekty specjalne filmów science fiction, gdzie jedynym ograniczeniem jest wyobraźnia twórców. Z drugiej strony systemy wspomagania projektowania dają dodatkowe możliwości wykonywania wielu obliczeń związanych bezpośrednio z dziedziną zastosowania – obliczeń konstrukcyjnych czy wytrzymałościowych. Oczywiście grafika komputerowa daje możliwość zobaczenia projektu – możliwość wizualizacji wyobrażeń projektanta. Niezbędne staje się narzędzie do modelowania kształtu – obiektu, powierzchni. Warto zwrócić uwagę na fakt, że użytkownicy takich systemów reprezentują różne poziomy przygotowania informatycznego. System modelowania powinien być więc prosty i efektywny, powinien dawać możliwość definicji kształtu za pomocą minimalnej liczby parametrów, a modyfikacja kształtu powinna dotyczyć wybranego fragmentu, a nie całości krzywej czy powierzchni. | ||
|} | |} | ||
---- | ---- | ||
| Linia 7: | Linia 7: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GK_M6n_Slajd2.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GK_M6n_Slajd2.png|thumb|500px]] | ||
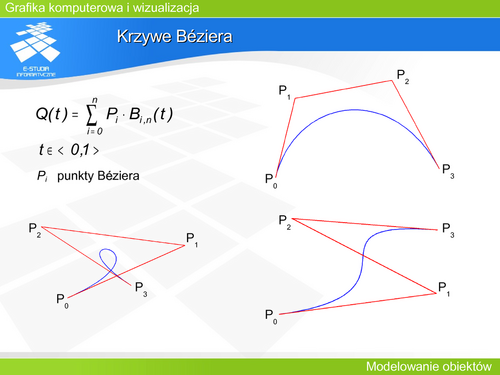
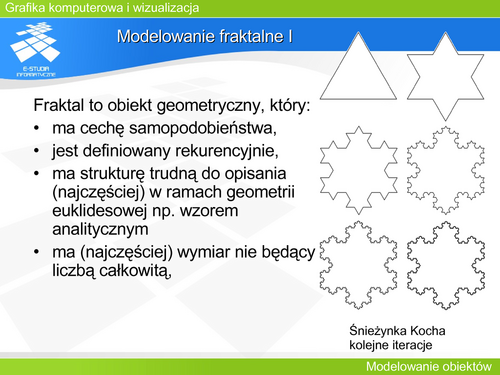
|valign="top"| | |valign="top"|W latach sześćdziesiątych XX wieku w fabryce Renault rozpoczął pracę pierwszy system modelowania geometrycznego na użytek komputerowego wspomagania projektowania. Twórcą tego systemu był P. Bézier – będący jedną z najważniejszych postaci w tej dziedzinie. Dzisiaj każda fabryka samochodów projektuje kształty karoserii wykorzystując modelowanie geometryczne. | ||
Istnieje wiele metod modelowania krzywych i powierzchni. Mają one różne właściwości i wymagają osobnego omówienia. | |||
|} | |} | ||
---- | ---- | ||
| Linia 14: | Linia 16: | ||
|width="500px" valign="top"|[[Grafika:GK_M6n_Slajd3.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GK_M6n_Slajd3.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
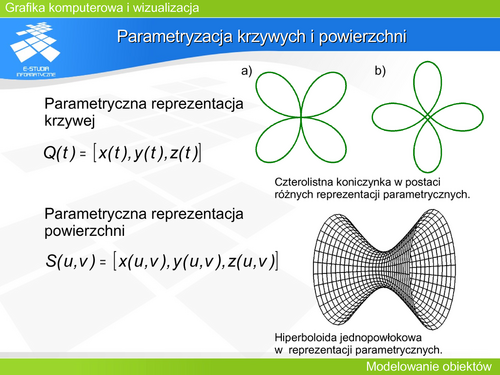
Wydawać by się mogło, że najprostszą forma modelowania krzywej jest wskazanie zbioru punktów na niej leżących a następnie połączenie ich krzywą interpolującą – najprościej wielomianową. | |||
Jeżeli dany jest ciąg parami różnych liczb <math>t_0, t_1, t_2, …t_n </math>– węzłów interpolacyjnych i odpowiadających im punktom <math>P_0, P_1, P_2,…P_n.</math> To poszukujemy krzywej wielomianowej P(t) takiej, że jest ona stopnia co najwyżej n oraz P(ti)=Pi dla każdego i. Tak sformułowane zadanie jest zadaniem interpolacyjnym Lagrange’a i ma dokładnie jedno rozwiązanie w postaci: | |||
<math>P(t)=\Sigma_{j=0 j\ne i}^n P_i( \prod_{j=0}^n \frac{t-t_j}{t_i-t_j})</math> | |||
Dla małej liczby punktów (kilku) uzyskana krzywa zachowuje się zgodnie z oczekiwaniem. Niestety dla większej liczby punktów – krzywa wykazuje bardzo dużą wrażliwość na zaburzenia węzłów i skłonność do oscylacji – co pokazuje rysunek a). Dodatkowo każdy fragment krzywej zależy od wszystkich węzłów – brak jest lokalnej reprezentacji. Problem oscylacji można rozwiązać korzystając z interpolacji krzywą sklejaną – przedziałami wielomianową niskiego stopnia, rysunek b). Jednak w obu przypadkach kontrola nad kształtem krzywej pomiędzy węzłami jest trudna. | |||
Wady te powodują, że takie rozwiązanie jest praktycznie nieprzydatne. | |||
|} | |} | ||
---- | ---- | ||
Wersja z 11:36, 17 lis 2006
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |