|
|
| Linia 99: |
Linia 99: |
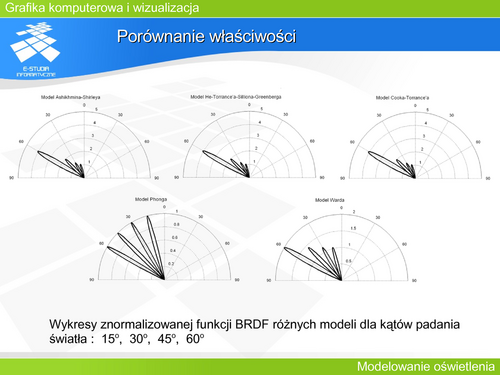
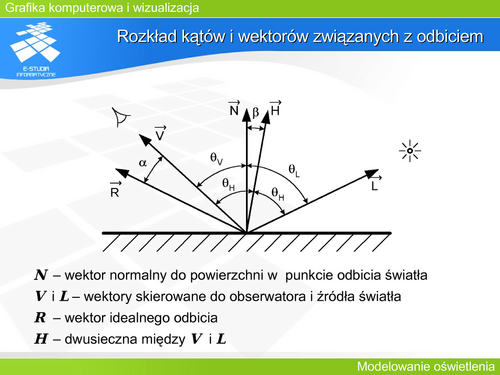
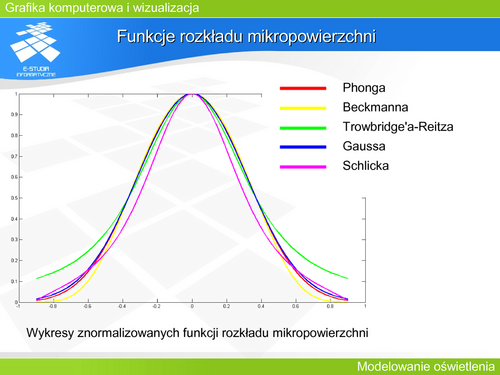
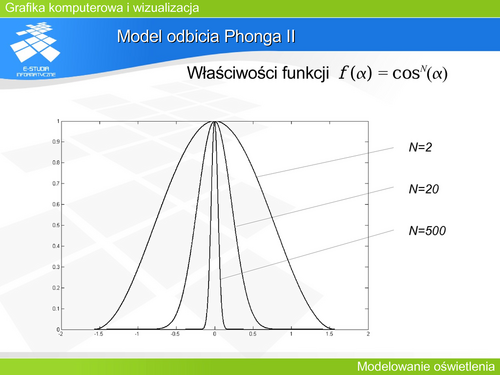
| O właściwościach kierunkowego odbicia w przyjętym modelu decyduje funkcja D rozkładu mikropowierzchni (czasami nazywana funkcją dystrybucji). D jest najczęściej funkcją kąta <math>\beta</math> (kąta <math>\alpha</math> w przypadku modelu Phonga). Spełnienie zasady zachowania energii wymaga, aby funkcja dystrybucji spełniała warunek normalizacji. Oznacza to dla powierzchni izotropowych następującą zależność: | | O właściwościach kierunkowego odbicia w przyjętym modelu decyduje funkcja D rozkładu mikropowierzchni (czasami nazywana funkcją dystrybucji). D jest najczęściej funkcją kąta <math>\beta</math> (kąta <math>\alpha</math> w przypadku modelu Phonga). Spełnienie zasady zachowania energii wymaga, aby funkcja dystrybucji spełniała warunek normalizacji. Oznacza to dla powierzchni izotropowych następującą zależność: |
|
| |
|
| <math>\int_{0}^{\pi /2}2 D(\beta) cos \beta sin \beta d\beta=1</math> | | <math>\int_{0}^{\pi /2}2 D(\beta) cos \beta sin \beta d\beta = 1</math> |
| | | |
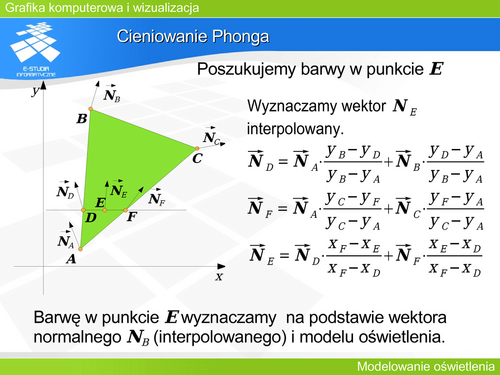
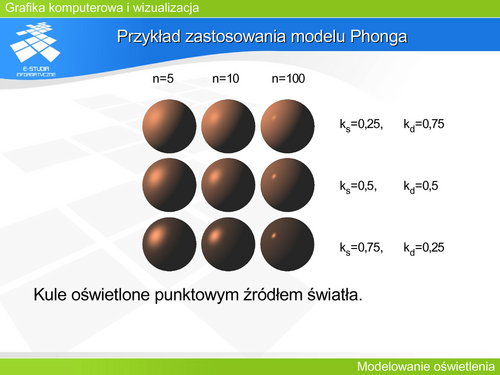
| Autorzy funkcji dystrybucji nie zawsze dbali o spełnienie tego warunku. Czasem dopiero niezależne prace późniejsze doprowadzały do spełnienia zasady zachowania energii – tak było np. w przypadku modelu odbicia Phonga. | | Autorzy funkcji dystrybucji nie zawsze dbali o spełnienie tego warunku. Czasem dopiero niezależne prace późniejsze doprowadzały do spełnienia zasady zachowania energii – tak było np. w przypadku modelu odbicia Phonga. |