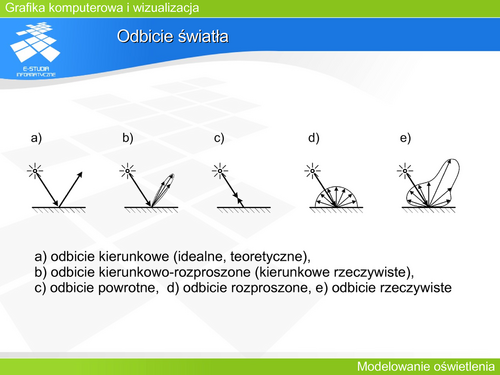
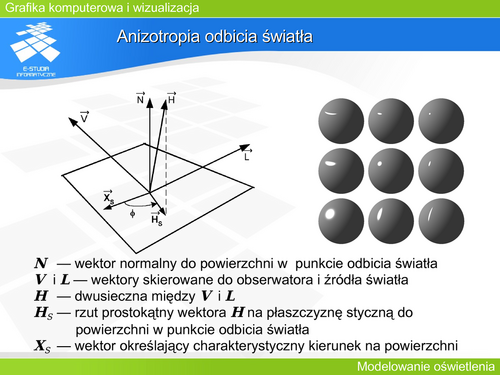
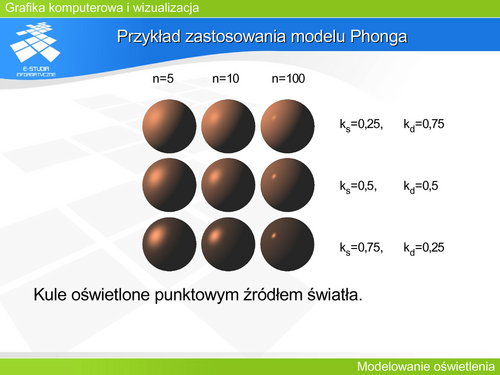
|
|
| Linia 205: |
Linia 205: |
| |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd31.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd31.png|thumb|500px]] |
| |valign="top"| | | |valign="top"| |
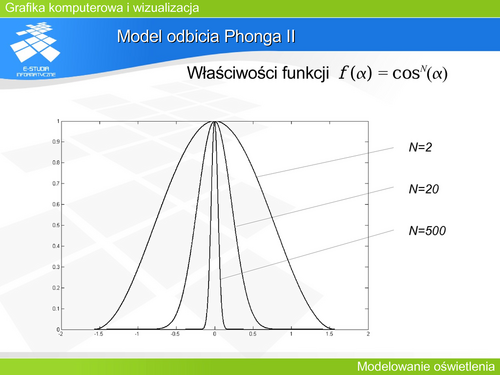
| Model odbicia Phonga II | | '''Model odbicia Phonga II''' |
|
| |
|
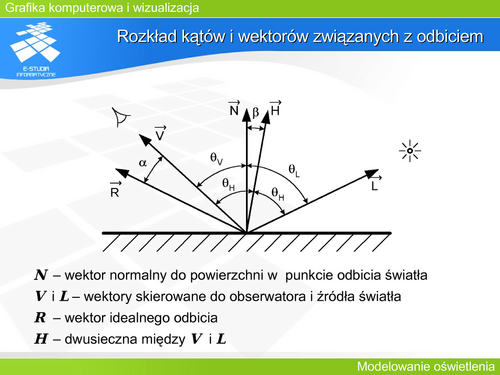
| Funkcja <math>cos^N(/alpha )</math> opisuje odbicie kierunkowe (zwierciadlane) przy czy N charakteryzuje dany materiał (właściwości odbiciowe powierzchni). Warto zwrócić uwagę na właściwości tej funkcji. Idealne odbicie kierunkowe to takie, w którym odbicie występuje tylko dla zerowego kąta <math>/alpha </math> (to znaczy poza tym kątem natężenie światła odbitego jest zerowe). Funkcja <math>cos^N(/alpha )</math> opisuje taki przypadek dla N dążącego do nieskończoności. Zatem im większa wartość N tym bardziej powierzchnia zbliża się do powierzchni lustrzanej. Tym lepsze właściwości kierunkowe charakteryzują odbicie od tej powierzchni. W praktyce już dla <math>N</math> rzędu kilkuset mamy do czynienia z dobrym lustrem. | | Funkcja <math>cos^N(/alpha )</math> opisuje odbicie kierunkowe (zwierciadlane) przy czy N charakteryzuje dany materiał (właściwości odbiciowe powierzchni). Warto zwrócić uwagę na właściwości tej funkcji. Idealne odbicie kierunkowe to takie, w którym odbicie występuje tylko dla zerowego kąta <math>/alpha </math> (to znaczy poza tym kątem natężenie światła odbitego jest zerowe). Funkcja <math>cos^N(/alpha )</math> opisuje taki przypadek dla N dążącego do nieskończoności. Zatem im większa wartość N tym bardziej powierzchnia zbliża się do powierzchni lustrzanej. Tym lepsze właściwości kierunkowe charakteryzują odbicie od tej powierzchni. W praktyce już dla <math>N</math> rzędu kilkuset mamy do czynienia z dobrym lustrem. |