PF Moduł 4

Wstęp Fizyka aspiruje do opisania przyrody w sposób uniwersalny. Oznacza to między innymi, że teorie fizyczne odnoszą się nie tylko do codziennej rzeczywistości (makroświat) ale i do zjawisk zachodzących na poziomie atomowym (mikroświat). Fizyka klasyczna, przez którą rozumiemy konsekwencje mechaniki Newtona i elektromagnetyzmu Maxwella, stosowana do opisu mikroświata (rozmiary mniejsze niż 10-10 m) okazała się dalece niewystarczająca. W mechanice uważa się, że materia składa się z cząstek obdarzonych masą, które poruszają się pod wpływem sił. Ruch takiej cząstki określony jest jej energią i wektorem pędu. W myśl teorii Maxwella zjawiska elektromagnetyczne można opisać za pomocą pola elektrycznego i pola magnetycznego. Pola te rozchodzą się w przestrzeni jako fale elektromagnetyczne charakteryzowane częstotliwością  i wektorem propagacji k. Cząstki i fale są odrębnymi składnikami przyrody. Taki obraz, w którym materia składa się cząstek a promieniowanie z fal stanowi podstawe do zadowalającego opisu makroświata. Okazuje się jednak, że opis taki jest zawodny w przypadku zjawisk zachodzących na poziomie mikrocząstek. Wobec tego należało zasadniczo zreformować teorię tak aby poglądy klasyczne, które są prawdziwe były naturalną konsekwencją teorii ogólniejszej, która nazywamy teorią kwantową.

---

Świecenie ciał czyli wypromieniowywanie fal elektromagnetycznych odbywa się kosztem różnego rodzaju energii. Najbardziej typowym jest promieniowanie termiczne odbywające się kosztem energii wewnętrznej ciał. Promieniowanie to emitowane jest w każdej temperaturze chociaż w niewielkich temperaturach ciała wysyłają jedynie długofalowe promieniowanie zwane podczerwonym. Jednocześnie zachodzi zjawisko odwrotne czyli absorbcja promieniowania przez ciało. Gdy ciało ma określoną temperaturę następuje równowaga między promieniowaniem a ciałem. Wówczas mamy do czynienia z charakterystycznym, zależnym od temperatury widmem promieniowania termicznego czyli rozkładem względnym natężeniem odpowiadającym różnym długościom fal elektromagnetycznych. Jeżeli temperatura jest odpowiednio wysoka (1500 K) w widmie pojawiają się nie tylko fale podczerwone ale również widzialne ( = 380 ÷ 550 nm), ciało zaczyna świecić. Istnieją dokładne metody pomiarowe wyznaczające widma promieniowania ciał w zależności od temperatury. Teoretyczne wyjaśnienie praw promieniowania miało doniosłe znaczenie w historii fizyki i doprowadziło do powstania pojęcia kwantów energii.

---

Rozważania teoretyczne zmierzające do wyjaśnienia widma promieniowania termicznego wychodziły z klasycznych teorii termodynamiki i elektromagnetyzmu. Uzyskane wyniki (Rayleigh – Jeans) okazały się całkowicie niezadowalające. Chociaż dość dobrze opisano dane doświadczalne dla małych długości fal to pojawiła się zasadnicza rozbieżność dla fal krótkich. Wynik ten znany jest jako „katastrofa w nadfiolecie” bowiem w obszarze tym gęstość promieniowania rośnie w myśl tych rozważań do nieskończoności.

---

W roku 1900 Planck znalazł funkcyjną postać gęstości wypromieniowanej energii w zależności od częstotliwości promieniowania i temperatury promieniującego ciała. Musiał w tym celu zrobić założenie, które było całkowicie sprzeczne z klasycznymi wyobrażeniami, a mianowicie musiał przyjąć, że promieniowanie elektromagnetyczne emitowane jest w postaci osobnych porcji energii, tzw. kwantów energii, o wartości proporcjonalnej do częstotliwości promieniowania: E = h. Współczynnik proporcjonalności h, nazwany później stałą Plancka został wyznaczony przez porównanie z danymi doświadczalnymi, $h=6.626\cdot 10^{-34}Js$. Otrzymany przez Plancka wzór daje wyczerpujący i w pełni zgodny z pomiarami opis zrównoważonego promieniowania termicznego. Jednocześnie wykracz poza granicę rozumienia promieniowania wyłącznie jako fali elektromagnetycznej. Słowa kluczowe promieniowanie termiczne – (thermal radiation) widmo promieniowania – (spectrum) emisja promieniowania – (radiation emission) kwant energii – (quantum) katastrofa nadfioletu – (ultraviolet catastrophe) stała Plancka – (Planck constant) wzór Plancka – (Planck radiation formula)

---

W metalu, który jest substancją przewodzącą, znajdują się swobodne elektrony. Są one swobodne ale tylko wewnątrz metalu gdyż nie mogą się wydostać na zewnątrz uwięzione w zagłębieniu potencjału elektrostatycznego. Można jednak doprowadzić do emisji elektronów dostarczając im energii wystarczającej do pokonania progu na powierzchni metalu. Przykładowo ogrzewając metal można doprowadzić do pokonania przez niektóre elektrony progu potencjału (tzw. termoemisja). Hertz badając fale elektromagnetyczne odkrył zjawisko wybijania elektronów z metalu również przez padające światło (tzw. fotoemisja). Zbadane potem cechy tego zjawiska, zjawiska fotoelektrycznego, okazały się zaskakujące i trudne do pogodzenia z teorią Maxwella stanowiącą fundament fizyki klasycznej.

---

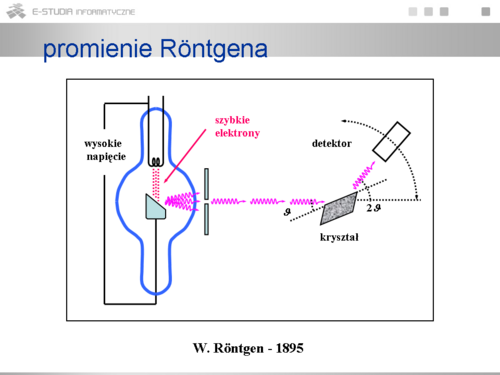
Zjawisko fotoelektryczne było zbadane przez Lenarda. W bańce próżniowej są zatopione dwie elektrody. Na jedną z nich (fotoelektrodę) skierowany jest strumień światła. Wytwarzając napięcie między elektrodami obserwuje się przepływ prądu. Czym są nośniki tego prądu płynącego przez próżnię? W polu magnetycznym odchylają się jak ładunki ujemne. Zmierzony stosunek ładunku do masy tych nośników wynosi: $e/m=1.76\cdot 10^{-11}C/kg$, co dowodzi że są to elektrony i niewątpliwie są to elektrony wybite z fotoelektrody. Ważną cechą zjawiska jest występowanie częstotliwości progowej. Światło wywołuje zjawisko fotoelektryczne tylko wówczas gdy jego częstotliwość przekracza pewną wartość charakterystyczną dla materiału, z którego zrobiona jest fotoelektroda. Dlaczego?

---

Prąd fotoelektryczny wykazuje swoiste właściwości: • Prąd płynie nawet wówczas gdy napięcie U między elektrodami jest równe zeru. • Natężenie prądu I rośnie wraz ze wzrostem napięcia ale wzrost ten następuje tylko do pewnej wartości i dalej natężenie pozostaje stałe. Występuje więc tzw. prąd nasycenia. • Natężenie prądu nasycenia rośnie ze wzrostem strumienia światła  padającego na fotoelektrodę. • Gdy napięcie między elektrodami jest przeciwne (ujemne wartości U) to prąd zanika. • Wartość ujemnego napięcia, przy którym prąd zanika całkowicie jest charakterystyczna i nie zależy od strumienia światła. Napięcie to nazywamy napięciem hamującym $U_0$. • Gdy do oświetlenia fotoelektrody stosujemy światło monochromatyczne to napięcie hamujące zależy od częstotliwości  padającego światła. Napięcie to rośnie wraz z częstotliwością. Powyższe cechy zjawiska fotoelektrycznego wymagają zrozumienia czyli opisu teoretycznego.

---

Einstein przyjmując ideę Plancka o kwantowym charakterze emisji i absorpcji światła podał równanie fotoelektryczne, które wyjaśniało omawiane zjawisko. Traktując monochromatyczne światło jako strumień fotonów o określonej energii Ef = hv rozumiemy, że pojedynczy foton albo odbija się od powierzchni metalu albo jest całkowicie pochłonięty przez pojedynczy elektron w metalu. Równanie fotoelektryczne stanowi bilans energetyczny takiego aktu pochłonięcia. Całkowita energia pochłoniętego fotonu może zostać zużyta na wydobycie elektronu z obszaru metalu (tzw. praca wyjścia W) a reszta tej energii stanowi energię kinetyczną elektronu wybitego z fotoelektrody.

---

Można teraz zrozumieć, że liczba emitowanych elektronów zależy od liczby pochłoniętych fotonów, czyli od strumienia pochłoniętego światła $\varphi$, a ich maksymalna energia kinetyczna zależy od energii fotonu Ef, czyli od częstotliwości światła, a tym samym od długości (barwy) monochromatycznego światła. Jeżeli częstotliwość jest zbyt mała to elektron nie może opuścić obszaru metalu i stąd występowanie częstotliwości progowej $nup$ poniżej której nie występuje zjawisko. Prąd nasycenia pojawia się dlatego, że przy określonym strumieniu powyżej pewnego napięcia wszystkie wybite elektrony docierają do elektrody zbierającej i natężenie prądu większe już być nie może, niezależnie od wzrostu napięcia. Oczywiste staje się też, że napięcie hamowania $U_0$ zależy od częstotliwości a nie od strumienia światła. Przy większej częstotliwości elektron charakteryzuje się większą energią kinetyczną i potrzebne jest większe napięcie aby zahamować jego ruch ku elektrodzie zbierającej.

---

Równanie fotoelektryczne określa liniową zależność energii kinetycznej elektronu emitowanego w zjawisku fotoelektrycznym od częstotliwości światła wywołującego to zjawisko. W przypadku danego światła monochromatycznego i określonej pracy wyjścia (zależy ona od materiału z którego wykonana jest fotoelektroda) maksymalna możliwa energia emitowanego elektronu E0 może być zmierzona. Określona jest ona przez napięcie hamujące i wynosi eU0 (jest to praca wykonana nad elementarnym ładunkiem e przy pokonaniu różnicy potencjałów, czyli napięcia U0). W swym doświadczeniu Millikan mierząc napięcia hamujące dla fotoelektrod wykonanych z różnych materiałów i przy różnej częstotliwości uzyskał: • liniowy charakter zależności, zgodny z równaniem fotoelektrycznym, • występowanie częstotliwości progowej $\nu p$ i jej pomiar w zależność od materiału fotoelektrody, • oszacowanie pracy wyjścia W dla różnych materiałów, • jednakowe nachylenie prostych niezależnie od materiału czyli uniwersalny charakter stałej Plancka. Doświadczenie pozwoliło na dokładne wyznaczenie tej stałej.

---

W swym ważnym doświadczeniu Millikan wykazał poprawność równania fotoelektrycznego Einsteina, które z kolei bazuje na hipotezie kwantowej Plancka. Dowodzi to fundamentalnej dwoistości natury światła. Jest ono z jednej strony falą elektromagnetyczną o czym świadczą zjawiska interferencji, dyfrakcji i polaryzacji. Z drugiej strony jest ono strumieniem bezmasowych kwantów energii promienistej, zwanych fotonami, o czym świadczą zjawiska związane z emisją i absorpcją światła. Jak wynika z tych pomiarów „granulacja” energii promienistej jest związana ze stałą Plancka. Wartość tej fundamentalnej stałej definiuje nam gdzie zaczyna się świat kwantowy. Stała ta jest bardzo mała i wynika z tego, że kwantowe jest to co jest małe, tak małe jak stała Planka. Należy podkreślić, że własności falowe fotonu nie są związane z jego występowaniem w intensywnych wiązkach. Jak wykazano w późniejszych badaniach własności falowe przejawia nawet pojedynczy foton (taki foton też doznaje dyfrakcji). To, że stała Planka jest stałą fundamentalną, definiującą nasz Świat oznacza, że nie wiemy dlaczego wynosi ona $h=6.67\cdot 10^{-32}Js$, możemy ją tylko zmierzyć i zrozumieć jakie znaczenia ma wartość tej stałej w budowie Świata. Często używa się we wzorach zmodyfikowanej stałej Parser nie mógł rozpoznać (błąd składni): {\displaystyle ħ = h/2\pi} . Wówczas energia fotonu wyraża się jako Parser nie mógł rozpoznać (błąd składni): {\displaystyle ħ\omega} , gdzie$\omega$ to tzw. częstość kołowa.

---

Podsumowując stwierdzamy, że zrozumienie zjawiska fotoelektryczne modyfikuje uproszczone, jednostronne rozumienie natury światła. Dodajmy, że podobną naturę wykazują i inne typy promieniowania elektromagnetycznego: fale radiowe, mikrofale, promienie Röntgena i gamma. Występują także pokrewne efekty w dielektrykach i półprzewodnikach, zwane wewnętrznym zjawiskiem fotoelektrycznym. Zjawiska te wiążą się z powszechnym zastosowaniem omawianego zjawiska w technice czyli z tzw. fotokomórką Słowa kluczowe zjawisko fotoelektryczne – (external) photoelectric effect fotoemisja elektronów – photoemission fotoelektroda – photocathode praca wyjścia – work function prąd nasycenia – saturation current napięcie hamujące – cut-off anode voltage foton - photon równanie fotoelektryczne Einsteina – Einstein photoelectric equation stala Plancka – Planck constant częstotliwość progowa – photoelectric threshold fotokomórka – photocell

---

Promienie rentgenowskie, odkryte przypadkowo a następnie zbadane przez W.Röntgena, powstają w lampie w której między żarzoną katodą a anodą przyłożone jest wysokie napięcie rzędu kilowoltów. Elektrony, które są emitowane z katody na skutek jej żarzenia są przyspieszane do dużych prędkości przez silne pole elektryczne. Następnie zderzają się z anodą i w wyniku tego powstają promienie o specyficznych własnościach. Są to promienie bardzo przenikliwe, nie posiadające ładunku. Promienie te mają naturę fali elektromagnetycznej o bardzo małej długości fali, w przedziale (5 \cdot 10^{-9} \div 1 \cdto 10^{-11} ) m, czyli kilka rzędów wielkości krótsze niż widzialne. Stwierdzenie falowej natury tak krótkich fal wymaga zastosowania szczególnych obiektów na których można zaobserwować efekty dyfrakcyjne. Chodzi mianowicie o rozpraszanie na krysztale. Typowe odległości między regularnie rozmieszczonymi w krysztale molekułami są rzędu $10^{-10}$ m a więc odpowiadają zakresowi długości fal rentgenowskich. Przy odbiciu od kryształu obserwuje się typowe dla fal sekwencje maksimów i można wyznaczyć długości fal i ich widma. Ale jaki mechanizm odpowiada za powstanie promieni rentgenowskich?

---

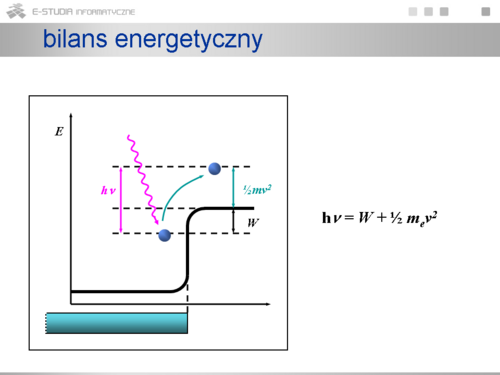
Otóż okazuje się, że szybkie elektrony zderzając się z metalową anodą silnie hamują w wewnątrzatomowym polu kulombowskim. Tracąc energię kinetyczną emitują kwanty promieniowania elektromagnetycznego (fotony). Bilans energetyczny takiego aktu pokazuje jaką częstotliwością charakteryzują się takie fotony (zgodnie z formułą Plancka). W oddziaływaniu tym bierze udział również jądro napotkanego atomu, które z uwagi na stosunkowo dużą masę przejmuje zaniedbywalną energię ale za to znaczny pęd. Umożliwia to emisję fotonu rentgenowskiego z zachowaniem bilansu pędowego. Czyli promieniowanie rentgenowskie jest promieniowaniem hamowania, z niemieckigo bremsstrahung

---

Widmo rentgenowskiego promieniowania hamowania jest widmem ciągłym i cechuje się występowaniem częstotliwości granicznej odpowiadającej krótkofalowej krawędzi widma. Krawędź krótkofalowa zależy od napięcia między elektrodami czyli od energii hamującego elektronu. Ciągłość widma związana jest z możliwością dowolnej utraty energii przez elektron a występowanie granicy wiąże się z zatrzymaniem elektronu czyli pełną utratą energii kinetycznej elektronu. W związku z tym zależność częstotliwości granicznej od napięcia między elektrodami jest zależnością liniową $h{\nu }_{max}=hc/{\lambda }_{min}=eU$. Dowodzi to ponownie kwantowego charakteru promieniowania elektromagnetycznego. Maksima widoczne w widmie przy najwyższym napięciu związane są z alternatywnym mechanizmem emisji fotonów rentgenowskich związanym z deekscytacją wzbudzonych atomów anody (tzw. charakterystyczne widmo liniowe).

---

Chociaż natura promieniowania elektromagnetycznego niezależnie od jego częstotliwości jest analogiczna jak też i jego własności kwantowe to należy zwrócić uwagę, są istotne różnice w oddziaływaniu z materią. W przypadku promieni Röntgena występuje silna zależność pochłaniania od składu atomowego ośrodka. Silniej pochłaniane są przez ciężkie atomy np. atomy wapnia w przypadku tkanki biologicznej co znajduje wyraz w zastosowaniach związanych z rentgenografią (prześwietlenia).

---

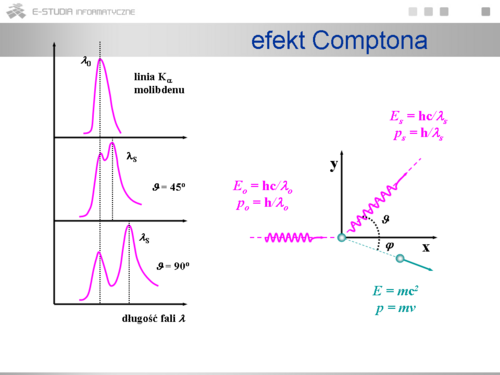
Efektem Comptona nazywamy rozpraszanie promieniowania rentgenowskiego na swobodnych elektronach. Okazuje się, że po rozproszeniu obserwuje się nie tylko składową o długości fali padającej ${\lambda }_o$ ale również składową o długości fali przesuniętej ku krótszym falom ${\lambda }_s$. Przesunięcie $\mathrm{\Delta }\lambda {=}_{\lambda }{}_s-{\lambda }_o$ zależne jest tylko od jednego parametru rozpraszania a mianowicie od kąta rozproszenia . Wyjaśnienie teoretyczne tego zjawiska prowadzi do wniosku, że foton charakteryzuje się niezerowym pędem. Na pozór jest to wniosek zaskakujący gdyż masa fotonu jest równa zeru. Mechanika relatywistyczna jednak przewiduje taką możliwość w odniesieniu do obiektów poruszających się z prędkością światła c.

---

Rozważmy zderzenie foton – elektron jako sprężyste zderzenie dwóch obiektów o określonej energii kinetycznej i pędzie. Po zderzeniu fotonu z nieruchomym elektronem zmienia się częstotliwość fotonu a elektron doznaje odrzutu. Skorzystajmy z zasad zachowania energii i pędu. zasada zachowania energii: $h{\nu }_o+m_e{c}^2=h{\nu }_s+m_e{c}^2+Ee$ $\to$ $Ee=h({\nu }_o-{\nu }_s)=(p_o-p_s)c$ zasada zachowania pędu: składowa y: Parser nie mógł rozpoznać (błąd składni): {\displaystyle ps sin = pe sin\phi} składowa x: Parser nie mógł rozpoznać (błąd składni): {\displaystyle po = ps cos + pe cos\phi} $\to$ Parser nie mógł rozpoznać (błąd składni): {\displaystyle p_o^2 - 2p_op_scos + p_s^2 = p_e^2} relatywistyczne wzory na całkowitą energię elektronu: $E=(m_e^{c}2{)}^2+(p_{e}c{)}^2$ $E=E_e+m_e{c}^2$ $\to$ $E_e^2+2E_e{m}_e{c}^2=p_e^2{c}^2$ otrzymujemy więc: Parser nie mógł rozpoznać (błąd składni): {\displaystyle h/p_s – h/p_o = h/m_ec \cdot (1 - cos)} Parser nie mógł rozpoznać (błąd składni): {\displaystyle \lambda_s - \lambda_o = h/m_ec \cdot (1 - cos)} Parser nie mógł rozpoznać (błąd składni): {\displaystyle \Delta\lambda = lambda_s - \lambda_o = \lambda_c(1 - cos)} gdzie ${\lambda }_c$ to stała zwana komptonowską długością fali: Parser nie mógł rozpoznać (błąd składni): {\displaystyle \lambda_c = h/m_ec = 2.426 \cdot 10^{-12} m.} uwaga: jeśli elektron, na którym rozprasza się foton jest elektronem silnie związanym w atomie to cały, ciężki atom doznaje odrzutu i masa w mianowniku jest masą atomu w rezultacie czego $\mathrm{\Delta }\lambda$ jest znikome. Stąd jest obecność fotonów o długości fali pierwotnej ${\lambda }_o$.

---

Równanie fotoelektryczne Einsteina, wzór Plancka, własności promieni Roentgena, analiza efektu Comptona i inne doświadczenia wykazały niezbicie że promieniowanie elektromagnetyczne ma dwoista naturę. Jest zarówno falą jak i strumieniem cząstek (korpuskuł). Opis falowy jest czymś przeciwnym do opisu korpuskularnego ale okazuje się, że promieniowanie jest i jednym i drugim. W 1924 r. de Broglie wysunął na pozór paradokaslną hipotezę, że dwoistość cechuje nie tylko zjawiska optyczne (w ogólości elektromagnetyczne) ale ma znaczenie uniwersalne, symetrycznie odnoszące się również do cząstek. Zakładając, że cząstki materii oprócz własności korpuskularnych mają także własności falowe de Broglie odwrócił reguły przechodzenia od obrazu falowego do cząsteczkowego na odwrotne. Przez analogię powiązał długość fali cząstki z jej pędem. Tak więc poruszająca się cząstka reprezentuje sobą falę materii. Chociaż rozważanie te miały charakter czysto teoretyczny to znalazły pełne potwierdzenie doświadczalne. Trzeba jednak zwrócić uwagę, ze zgodnie z hipotezą de Broglie’a obiekty makroskopowe cechują się tak małymi długościami fali, że nie ma możliwości potwierdzenia ich natury falowej. Inaczej sprawa się przedstawia w przypadku mikrocząstek, np. elektronów...

---

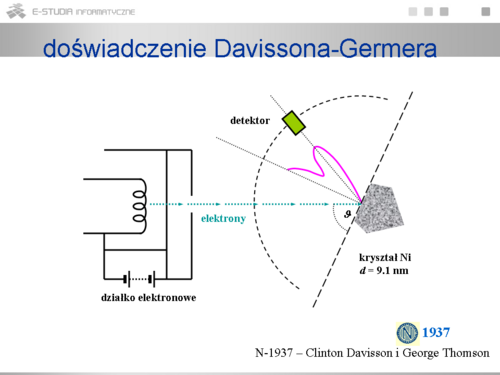
Hipoteza de Broglie’a po raz pierwszy została sprawdzona w 1927 r. doświadczalnie. Doświadczenie to polegało na rozpraszaniu niskoenergetycznych elektronów na powierzchni monokryształu metalu. Regularnie rozłożone rzędy atomów na powierzchni monokryształu pełnią rolę szczelin bardzo drobnej siatki dyfrakcyjnej. Długość fali materii przewidzianej przez de Broglie’a dla powolnego elektronu odpowiada właśnie odległościom międzyatomowym w krysztale (stała siatki). Jest to oczywiście warunek wystąpienia zjawiska dyfrakcji charakterystycznego dla zjawisk falowych. Co więcej długość fali elektronu można wyznaczyć doświadczalnie znając stałą siatki krystalicznej i analizując obraz dyfrakcyjny. Obraz dyfrakcyjny wiązki elektronów potwierdza całkowicie falową naturę materii przewidzianą teoretycznie przez de Broglie’a. Dodać należy, że jak później wykazano, własności dyfrakcyjne wykazuje również pojedynczy elektron a więc falowe własności elektronu nie są związane z wiązką ale z samą cząstką.

---

Promieniowanie elektromagnetyczne oddziałuje z ośrodkiem w różny sposób przejawiając swe własności korpuskularne. Może nastąpić pochłonięcie fotonu przez elektron (zjawisko fotoelektryczne), może nastąpić rozproszenie fotonu ze zmianą długości fali (efekt Comptona). Dodatkowo, w przypadku gdy foton ma dostatecznie dużą energię, może zajść jeszcze inne zjawisko. Otóż może on zmienić się całkowicie w masę kreując dwie cząstki, a mianowicie elektron i pozyton. Obojętny elektrycznie foton wytwarzając ujemny elektron musi jednocześnie wykreować cząstkę dodatnią (zasada zachowania ładunku). Jest nią dodatni elektron czyli antyelektron (cząstka antymaterii) zwany pozytonem. Pozyton nie występuje w zwykłej materii. To, że masa jest równoważna energii, na przykład energii promienistej, wynika z relatywistycznej teorii Einsteina E = m0c2. Energia niesiona przez foton zamienia się więc w równoważną jej masę dwóch cząstek. A pęd fotonu? Oczywiście nie może zniknąć (zasada zachowania pędu), nie może też być w całości przekazany wtórnym cząstkom gdyż mogą one powstać również w spoczynku, z zerowym pędem. Dlatego też zjawisko kreacji zachodzi tylko w ośrodku, gdzie nadmiar pędu może być przejęty przez okoliczne, ciężkie jądro atomu. Ponieważ masa elektronu jak i identyczna masa pozytonu wynosi $me=0.511MeV/c^2$ to oczywiście zjawisko to występuje tylko w przypadku fotonów o energii przewyższającej milion elektronowoltów. Takie promieniowanie nazywa się promieniowaniem gamma $(\gamma )$.

---

Powstaje pytanie jakie są losy pozytonu powstałego w wyniku zjawiska kreacji, czy też jakiejkolwiek wytworzonej antycząstki. Otóż jak każda poruszająca się w ośrodku materialnym naładowana cząstka (pozyton obdarzony jest dodatnim elementarnym ładunkiem) doznaje procesu hamowania. Hamowanie to odbywa się w wyniku jonizacji ośrodka czyli systematycznej utraty energii kinetycznej przekazywanej napotkanym atomom w wyniku czego elektrony wybijane są z orbit atomowych. Pozyton w krótkim czasie zatrzymuje się i tworzy układ związany z okolicznym elektronem (tzw. pozytonium) po czym następuje anihilacja obu cząstek. Zdolność do anihilacji wykazują jedynie antycząstki, jest to więc proces egzotyczny, zachodzący wyjątkowo tylko wtedy gdy powstanie antycząstka. Anihilacja polega na tym, że obie cząstki, cząstka i antycząstka, znikają a energia równoważna ich masie zamienia się w energię dwóch fotonów. Dlaczego dwóch? Ponieważ pęd początkowy spoczywających cząstek jest równy zeru więc i końcowy musi być równy zeru. Stąd w wyniku procesu powstają dwa fotony o równych energiach lecące w przeciwne strony. Słowa kluczowe dualizm korpuskularno falowy – wave-particle duality fale materii, fale de Broglie’a – matter waves, de Broglie waves rozpraszanie dyfrakcyjne – diffractive scattering kreacja pary – pair production antymateria, antycząstka – antimatter, antiparticle pozyton – positron, positon anihilacja – annihilation promieniowanie gamma – gamma radiation jonizacja – ionisation

---