PF Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd1.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd1.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Wstęp | ||
Fizyka aspiruje do opisania przyrody w sposób uniwersalny. Oznacza to między innymi, że teorie fizyczne odnoszą się nie tylko do codziennej rzeczywistości (makroświat) ale i do zjawisk zachodzących na poziomie atomowym (mikroświat). Fizyka klasyczna, przez którą rozumiemy konsekwencje mechaniki Newtona i elektromagnetyzmu Maxwella, stosowana do opisu mikroświata (rozmiary mniejsze niż 10-10 m) okazała się dalece niewystarczająca. | |||
W mechanice uważa się, że materia składa się z cząstek obdarzonych masą, które poruszają się pod wpływem sił. Ruch takiej cząstki określony jest jej energią i wektorem pędu. | |||
W myśl teorii Maxwella zjawiska elektromagnetyczne można opisać za pomocą pola elektrycznego i pola magnetycznego. Pola te rozchodzą się w przestrzeni jako fale elektromagnetyczne charakteryzowane częstotliwością i wektorem propagacji k. Cząstki i fale są odrębnymi składnikami przyrody. | |||
Taki obraz, w którym materia składa się cząstek a promieniowanie z fal stanowi podstawe do zadowalającego opisu makroświata. Okazuje się jednak, że opis taki jest zawodny w przypadku zjawisk zachodzących na poziomie mikrocząstek. Wobec tego należało zasadniczo zreformować teorię tak aby poglądy klasyczne, które są prawdziwe były naturalną konsekwencją teorii ogólniejszej, która nazywamy teorią kwantową. | |||
|} | |} | ||
---- | ---- | ||
| Linia 7: | Linia 15: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd2.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd2.png|thumb|500px]] | ||
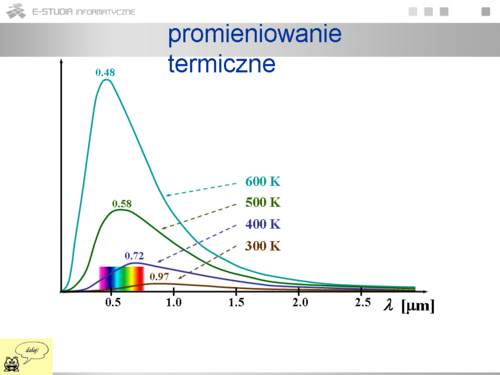
|valign="top"| | |valign="top"|Świecenie ciał czyli wypromieniowywanie fal elektromagnetycznych odbywa się kosztem różnego rodzaju energii. Najbardziej typowym jest promieniowanie termiczne odbywające się kosztem energii wewnętrznej ciał. Promieniowanie to emitowane jest w każdej temperaturze chociaż w niewielkich temperaturach ciała wysyłają jedynie długofalowe promieniowanie zwane podczerwonym. Jednocześnie zachodzi zjawisko odwrotne czyli absorbcja promieniowania przez ciało. Gdy ciało ma określoną temperaturę następuje równowaga między promieniowaniem a ciałem. Wówczas mamy do czynienia z charakterystycznym, zależnym od temperatury widmem promieniowania termicznego czyli rozkładem względnym natężeniem odpowiadającym różnym długościom fal elektromagnetycznych. Jeżeli temperatura jest odpowiednio wysoka (1500 K) w widmie pojawiają się nie tylko fale podczerwone ale również widzialne ( = 380 ÷ 550 nm), ciało zaczyna świecić. Istnieją dokładne metody pomiarowe wyznaczające widma promieniowania ciał w zależności od temperatury. Teoretyczne wyjaśnienie praw promieniowania miało doniosłe znaczenie w historii fizyki i doprowadziło do powstania pojęcia kwantów energii. | ||
|} | |} | ||
---- | ---- | ||
| Linia 13: | Linia 21: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd3.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd3.png|thumb|500px]] | ||
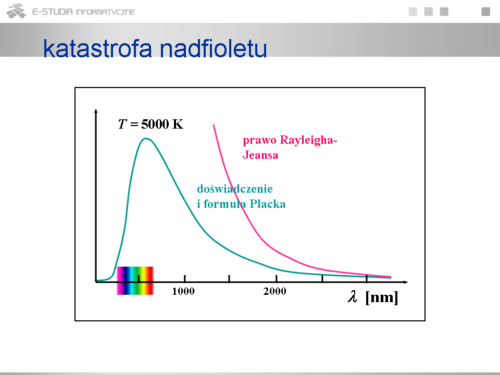
|valign="top"| | |valign="top"|Rozważania teoretyczne zmierzające do wyjaśnienia widma promieniowania termicznego wychodziły z klasycznych teorii termodynamiki i elektromagnetyzmu. Uzyskane wyniki (Rayleigh – Jeans) okazały się całkowicie niezadowalające. Chociaż dość dobrze opisano dane doświadczalne dla małych długości fal to pojawiła się zasadnicza rozbieżność dla fal krótkich. Wynik ten znany jest jako „katastrofa w nadfiolecie” bowiem w obszarze tym gęstość promieniowania rośnie w myśl tych rozważań do nieskończoności. | ||
|} | |} | ||
---- | ---- | ||
| Linia 19: | Linia 29: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd4.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd4.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|W roku 1900 Planck znalazł funkcyjną postać gęstości wypromieniowanej energii w zależności od częstotliwości promieniowania i temperatury promieniującego ciała. Musiał w tym celu zrobić założenie, które było całkowicie sprzeczne z klasycznymi wyobrażeniami, a mianowicie musiał przyjąć, że promieniowanie elektromagnetyczne emitowane jest w postaci osobnych porcji energii, tzw. kwantów energii, o wartości proporcjonalnej do częstotliwości promieniowania: E = h. Współczynnik proporcjonalności h, nazwany później stałą Plancka został wyznaczony przez porównanie z danymi doświadczalnymi, <math>h = 6.626 \cdot 10^{-34} Js</math>. Otrzymany przez Plancka wzór daje wyczerpujący i w pełni zgodny z pomiarami opis zrównoważonego promieniowania termicznego. Jednocześnie wykracz poza granicę rozumienia promieniowania wyłącznie jako fali elektromagnetycznej. | ||
'''Słowa kluczowe''' | |||
promieniowanie termiczne – (thermal radiation) | |||
widmo promieniowania – (spectrum) | |||
emisja promieniowania – (radiation emission) | |||
kwant energii – (quantum) | |||
katastrofa nadfioletu – (ultraviolet catastrophe) | |||
stała Plancka – (Planck constant) | |||
wzór Plancka – (Planck radiation formula) | |||
|} | |} | ||
---- | ---- | ||
| Linia 25: | Linia 52: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd5.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd5.png|thumb|500px]] | ||
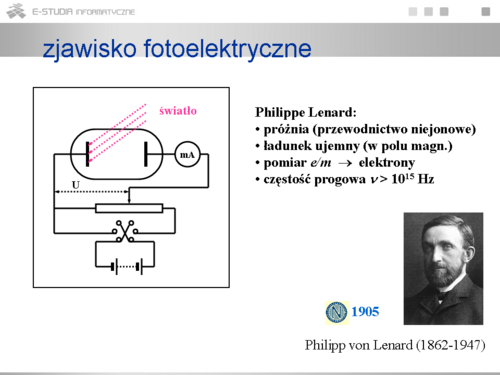
|valign="top"| | |valign="top"|W metalu, który jest substancją przewodzącą, znajdują się swobodne elektrony. Są one swobodne ale tylko wewnątrz metalu gdyż nie mogą się wydostać na zewnątrz uwięzione w zagłębieniu potencjału elektrostatycznego. Można jednak doprowadzić do emisji elektronów dostarczając im energii wystarczającej do pokonania progu na powierzchni metalu. Przykładowo ogrzewając metal można doprowadzić do pokonania przez niektóre elektrony progu potencjału (tzw. termoemisja). Hertz badając fale elektromagnetyczne odkrył zjawisko wybijania elektronów z metalu również przez padające światło (tzw. fotoemisja). Zbadane potem cechy tego zjawiska, zjawiska fotoelektrycznego, okazały się zaskakujące i trudne do pogodzenia z teorią Maxwella stanowiącą fundament fizyki klasycznej. | ||
|} | |} | ||
---- | ---- | ||
| Linia 31: | Linia 58: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd6.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd6.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Zjawisko fotoelektryczne było zbadane przez Lenarda. W bańce próżniowej są zatopione dwie elektrody. Na jedną z nich (fotoelektrodę) skierowany jest strumień światła. Wytwarzając napięcie między elektrodami obserwuje się przepływ prądu. Czym są nośniki tego prądu płynącego przez próżnię? W polu magnetycznym odchylają się jak ładunki ujemne. Zmierzony stosunek ładunku do masy tych nośników wynosi: <math> e/m = 1.76 \cdot 10^{-11} C/kg</math>, co dowodzi że są to elektrony i niewątpliwie są to elektrony wybite z fotoelektrody. Ważną cechą zjawiska jest występowanie częstotliwości progowej. Światło wywołuje zjawisko fotoelektryczne tylko wówczas gdy jego częstotliwość przekracza pewną wartość charakterystyczną dla materiału, z którego zrobiona jest fotoelektroda. Dlaczego? | ||
|} | |} | ||
---- | ---- | ||
| Linia 38: | Linia 65: | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd7.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd7.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
Prąd fotoelektryczny wykazuje swoiste właściwości: | |||
• Prąd płynie nawet wówczas gdy napięcie U między elektrodami jest równe zeru. | |||
• Natężenie prądu I rośnie wraz ze wzrostem napięcia ale wzrost ten następuje tylko do pewnej wartości i dalej natężenie pozostaje stałe. Występuje więc tzw. prąd nasycenia. | |||
• Natężenie prądu nasycenia rośnie ze wzrostem strumienia światła padającego na fotoelektrodę. | |||
• Gdy napięcie między elektrodami jest przeciwne (ujemne wartości U) to prąd zanika. | |||
• Wartość ujemnego napięcia, przy którym prąd zanika całkowicie jest charakterystyczna i nie zależy od strumienia światła. Napięcie to nazywamy napięciem hamującym <math>U_0</math>. | |||
• Gdy do oświetlenia fotoelektrody stosujemy światło monochromatyczne to napięcie hamujące zależy od częstotliwości padającego światła. Napięcie to rośnie wraz z częstotliwością. | |||
Powyższe cechy zjawiska fotoelektrycznego wymagają zrozumienia czyli opisu teoretycznego. | |||
|} | |} | ||
---- | ---- | ||
| Linia 43: | Linia 86: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd8.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd8.png|thumb|500px]] | ||
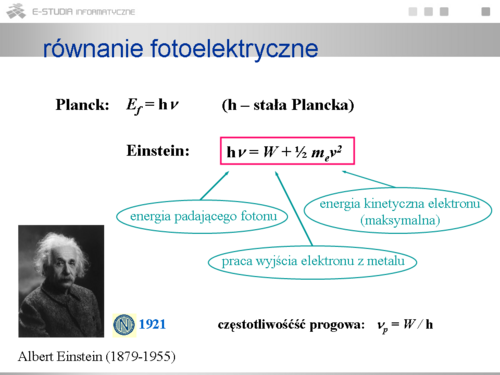
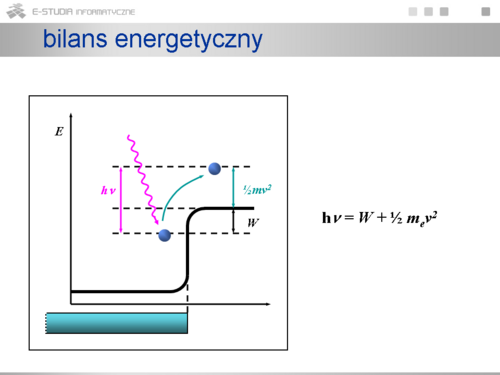
|valign="top"| | |valign="top"|Einstein przyjmując ideę Plancka o kwantowym charakterze emisji i absorpcji światła podał równanie fotoelektryczne, które wyjaśniało omawiane zjawisko. Traktując monochromatyczne światło jako strumień fotonów o określonej energii Ef = hv rozumiemy, że pojedynczy foton albo odbija się od powierzchni metalu albo jest całkowicie pochłonięty przez pojedynczy elektron w metalu. Równanie fotoelektryczne stanowi bilans energetyczny takiego aktu pochłonięcia. Całkowita energia pochłoniętego fotonu może zostać zużyta na wydobycie elektronu z obszaru metalu (tzw. praca wyjścia W) a reszta tej energii stanowi energię kinetyczną elektronu wybitego z fotoelektrody. | ||
|} | |} | ||
---- | ---- | ||
| Linia 49: | Linia 92: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd9.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd9.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Można teraz zrozumieć, że liczba emitowanych elektronów zależy od liczby pochłoniętych fotonów, czyli od strumienia pochłoniętego światła <math>\phi</math>, a ich maksymalna energia kinetyczna zależy od energii fotonu Ef, czyli od częstotliwości światła, a tym samym od długości (barwy) monochromatycznego światła. Jeżeli częstotliwość jest zbyt mała to elektron nie może opuścić obszaru metalu i stąd występowanie częstotliwości progowej <math>nu p</math> poniżej której nie występuje zjawisko. Prąd nasycenia pojawia się dlatego, że przy określonym strumieniu powyżej pewnego napięcia wszystkie wybite elektrony docierają do elektrody zbierającej i natężenie prądu większe już być nie może, niezależnie od wzrostu napięcia. Oczywiste staje się też, że napięcie hamowania <math>U_0</math> zależy od częstotliwości a nie od strumienia światła. Przy większej częstotliwości elektron charakteryzuje się większą energią kinetyczną i potrzebne jest większe napięcie aby zahamować jego ruch ku elektrodzie zbierającej. | ||
|} | |} | ||
---- | ---- | ||
| Linia 55: | Linia 98: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd10.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd10.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Równanie fotoelektryczne określa liniową zależność energii kinetycznej elektronu emitowanego w zjawisku fotoelektrycznym od częstotliwości światła wywołującego to zjawisko. W przypadku danego światła monochromatycznego i określonej pracy wyjścia (zależy ona od materiału z którego wykonana jest fotoelektroda) maksymalna możliwa energia emitowanego elektronu E0 może być zmierzona. Określona jest ona przez napięcie hamujące i wynosi eU0 (jest to praca wykonana nad elementarnym ładunkiem e przy pokonaniu różnicy potencjałów, czyli napięcia U0). W swym doświadczeniu Millikan mierząc napięcia hamujące dla fotoelektrod wykonanych z różnych materiałów i przy różnej częstotliwości uzyskał: | ||
• liniowy charakter zależności, zgodny z równaniem fotoelektrycznym, | |||
• występowanie częstotliwości progowej <math>\nu p</math> i jej pomiar w zależność od materiału fotoelektrody, | |||
• oszacowanie pracy wyjścia W dla różnych materiałów, | |||
• jednakowe nachylenie prostych niezależnie od materiału czyli uniwersalny | |||
charakter stałej Plancka. Doświadczenie pozwoliło na dokładne wyznaczenie tej stałej. | |||
|} | |} | ||
---- | ---- | ||
| Linia 61: | Linia 115: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd11.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd11.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|W swym ważnym doświadczeniu Millikan wykazał poprawność równania fotoelektrycznego | ||
Einsteina, które z kolei bazuje na hipotezie kwantowej Plancka. Dowodzi to fundamentalnej dwoistości natury światła. Jest ono z jednej strony falą elektromagnetyczną o czym świadczą zjawiska interferencji, dyfrakcji i polaryzacji. Z drugiej strony jest ono strumieniem bezmasowych kwantów energii promienistej, zwanych fotonami, o czym świadczą zjawiska związane z emisją i absorpcją światła. Jak wynika z tych pomiarów „granulacja” energii promienistej jest związana ze stałą Plancka. Wartość tej fundamentalnej stałej definiuje nam gdzie zaczyna się świat kwantowy. Stała ta jest bardzo mała i wynika z tego, że kwantowe jest to co jest małe, tak małe jak stała Planka. Należy podkreślić, że własności falowe fotonu nie są związane z jego występowaniem w intensywnych wiązkach. Jak wykazano w późniejszych badaniach własności falowe przejawia nawet pojedynczy foton (taki foton też doznaje dyfrakcji). To, że stała Planka jest stałą fundamentalną, definiującą nasz Świat oznacza, że nie wiemy dlaczego wynosi ona <math>h = 6.67 \cdot 10^{-32} Js</math>, możemy ją tylko zmierzyć i zrozumieć jakie znaczenia ma wartość tej stałej w budowie Świata. Często używa się we wzorach zmodyfikowanej stałej <math>ħ = h/2\pi</math>. Wówczas energia fotonu wyraża się jako <math>ħ\omega</math>, gdzie<math> \omega</math> to tzw. częstość kołowa. | |||
|} | |} | ||
---- | ---- | ||
| Linia 67: | Linia 123: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd12.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd12.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Podsumowując stwierdzamy, że zrozumienie zjawiska fotoelektryczne modyfikuje | ||
uproszczone, jednostronne rozumienie natury światła. Dodajmy, że podobną naturę wykazują i inne typy promieniowania elektromagnetycznego: fale radiowe, mikrofale, promienie Röntgena i gamma. Występują także pokrewne efekty w dielektrykach i półprzewodnikach, zwane wewnętrznym zjawiskiem fotoelektrycznym. Zjawiska te wiążą się z powszechnym zastosowaniem omawianego zjawiska w technice czyli z tzw. fotokomórką | |||
Słowa kluczowe | |||
zjawisko fotoelektryczne – (external) photoelectric effect | |||
fotoemisja elektronów – photoemission | |||
fotoelektroda – photocathode | |||
praca wyjścia – work function | |||
prąd nasycenia – saturation current | |||
napięcie hamujące – cut-off anode voltage | |||
foton - photon | |||
równanie fotoelektryczne Einsteina – Einstein photoelectric equation | |||
stala Plancka – Planck constant | |||
częstotliwość progowa – photoelectric threshold | |||
fotokomórka – photocell | |||
|} | |} | ||
---- | ---- | ||
| Linia 73: | Linia 156: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd13.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd13.png|thumb|500px]] | ||
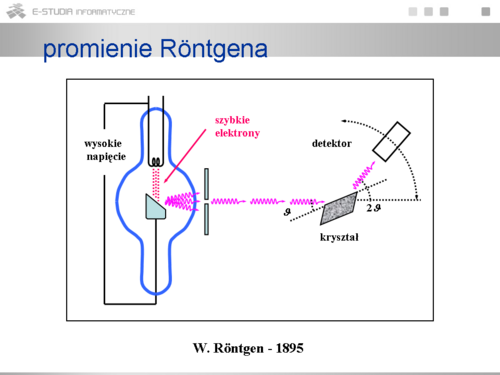
|valign="top"| | |valign="top"|Promienie rentgenowskie, odkryte przypadkowo a następnie zbadane przez W.Röntgena, powstają w lampie w której między żarzoną katodą a anodą przyłożone jest wysokie napięcie rzędu kilowoltów. Elektrony, które są emitowane z katody na skutek jej żarzenia są przyspieszane do dużych prędkości przez silne pole elektryczne. Następnie zderzają się z anodą i w wyniku tego powstają promienie o specyficznych własnościach. Są to promienie bardzo przenikliwe, nie posiadające ładunku. Promienie te mają naturę fali elektromagnetycznej o bardzo małej długości fali, w przedziale (5 \cdot 10^{-9} 1 10-11 ) m, czyli kilka rzędów wielkości krótsze niż widzialne. Stwierdzenie falowej natury tak krótkich fal wymaga zastosowania szczególnych obiektów na których można zaobserwować efekty dyfrakcyjne. Chodzi mianowicie o rozpraszanie na krysztale. Typowe odległości między regularnie rozmieszczonymi w krysztale molekułami są rzędu 10-10 m a więc odpowiadają zakresowi długości fal rentgenowskich. Przy odbiciu od kryształu obserwuje się typowe dla fal sekwencje maksimów i można wyznaczyć długości fal i ich widma. Ale jaki mechanizm odpowiada za powstanie promieni rentgenowskich? | ||
|} | |} | ||
---- | ---- | ||
Wersja z 13:54, 12 paź 2006
 |
 |
 |
 |
 |
 |
 |
 |
 |