SW wykład 11 - Slajd7: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 2: | Linia 2: | ||
[[Grafika:sw1106.png|frame|center|]] | [[Grafika:sw1106.png|frame|center|]] | ||
Stwierdzenia o częściowej poprawności instrukcji uogólnionego języka | |||
TINY wprowadzamy i definiujemy ich prawdziwość dokładnie tak, jak | |||
poprzednio. Uwaga jednak: oczywiście, formuły pierwszego rzędu | |||
wykorzystują teraz wyrażenia logiczne zmodyfikowanego języka, a więc | |||
mówią o stanach wartościujących zmienne w nośnik algebry modelującej | |||
pierwotny typ danych, używając predykatów podanych w sygnaturze tego | |||
typu. | |||
Zachowujemy też dokładnie reguły dowodzenia dla logiki Hoare'a, jak | |||
podane one zostały na slajdzie 9 poprzedniego wykładu. Oczywiście, | |||
implikacje wykorzystywane w regule wynikania mówią teraz o warunkach | |||
dotyczących algebry pierwotnego typu danych, nie o modelu liczb | |||
całkowitych. I właśnie z formuł prawdziwych w tej algebrze możemy | |||
teraz korzystać w dowodach prowadzonych w tym systemie dowodzenia dla | |||
logiki Hoare'a. | |||
Nadal zachodzi twierdzenie o poprawności tak określonego systemu | |||
dowodzenia dla logiki Hoare'a (dowód bez istotnych zmian w stosunku do | |||
dowodu poprawności dla początkowej wersji języka TINY operującej na | |||
typie liczb całkowitych). | |||
Aktualna wersja na dzień 17:12, 10 paź 2006
Poprawność systemu dowodzenia Hoare'a Dowód Dowód, c.d. Problem z pełnością Uogólnienie TINY TINY Ekspresywność Relatywna pełność logiki Hoare'a Rozszerzenia Ograniczenia
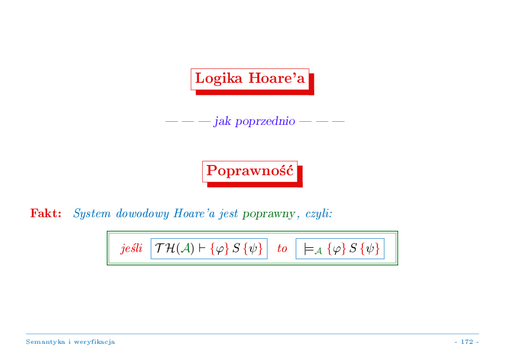
Stwierdzenia o częściowej poprawności instrukcji uogólnionego języka TINY wprowadzamy i definiujemy ich prawdziwość dokładnie tak, jak poprzednio. Uwaga jednak: oczywiście, formuły pierwszego rzędu wykorzystują teraz wyrażenia logiczne zmodyfikowanego języka, a więc mówią o stanach wartościujących zmienne w nośnik algebry modelującej pierwotny typ danych, używając predykatów podanych w sygnaturze tego typu.
Zachowujemy też dokładnie reguły dowodzenia dla logiki Hoare'a, jak podane one zostały na slajdzie 9 poprzedniego wykładu. Oczywiście, implikacje wykorzystywane w regule wynikania mówią teraz o warunkach dotyczących algebry pierwotnego typu danych, nie o modelu liczb całkowitych. I właśnie z formuł prawdziwych w tej algebrze możemy teraz korzystać w dowodach prowadzonych w tym systemie dowodzenia dla logiki Hoare'a.
Nadal zachodzi twierdzenie o poprawności tak określonego systemu dowodzenia dla logiki Hoare'a (dowód bez istotnych zmian w stosunku do dowodu poprawności dla początkowej wersji języka TINY operującej na typie liczb całkowitych).