SW wykład 11 - Slajd5

<<powrót do strony wykładu

Poprawność systemu dowodzenia Hoare'a Dowód Dowód, c.d. Problem z pełnością Uogólnienie TINY${}_A$ TINY${}_A$ Ekspresywność Relatywna pełność logiki Hoare'a Rozszerzenia Ograniczenia

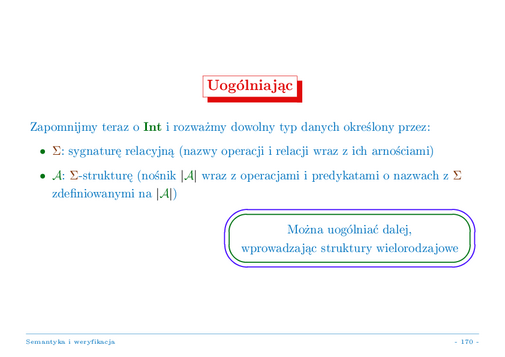
Zapomnijmy więc na chwilę, że nasz język TINY był definiowany dla bardzo konkretnego typu danych: liczb całkowitych z zadaną listą operacji arytmetycznych i predykatów. Uogólnijmy to, przyjmując, że będziemy teraz pracować z dowolnym wbudowanym pierwotnym typem danych. To znaczy, definicję języka zacznijmy od podania sygnatury tego pierwotnego typu danych, która określa pewien zbiór nazw operacji i nazw predykatów (z ich arnością --- tzn., podając liczbę ich argumentów). Następnie ustalamy pewną algebrę nad tą sygnaturą: zbiór wartości (nośnik algebry) i dla każdej nazwy operacji, funkcję na tym zbiorze, a dla każdej nazwy predykatu, relację na tym zbiorze (o odpowiedniej, zgodnej z podaną w sygnaturze, liczbie argumentów). Algebra ta interpretuje semantycznie nasz pierwotny typ danych języka; nazywać ją będziemy algebrą pierwotnego typu danych.

Całą definicję języka i dalszą analizę łatwo uogólnić dalej, dopuszczając tu bardziej realistyczny przypadek sygnatur i algebr wielorodzajowych, gdzie zbiór danych jest podzielony na wiele rodzajów nazwanych w sygnaturze, a arność operacji i predykatów określa nie tylko liczbę, ale i rodzaj ich poszczególnych argumentów (plus rodzaj wyniku dla operacji). Nie będziemy tu dalej analizować tego "wielorodzajowego" uogólnienia.