MO Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 44: | Linia 44: | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd7.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd7.png|thumb|500px]] | ||
|valign="top"|Algorytm może być: | |valign="top"|Algorytm może być: | ||
*'''ostrożny''' (wiem, że schody opadają w prawo, schodzę w prawo jeden stopień) i przyjąć <math>x^{M(k)}</math> za środek nowego otoczenia<br><math>x^{(k+1)}=x^{M(k)}=\alpha (x^{M(k)}-x^{(k)})+x^{(k)}, \alpha=1</math>, | *'''ostrożny''' (wiem, że schody opadają w prawo, schodzę w prawo jeden stopień) i przyjąć <math>x^{\mathrm {M}(k)}</math> za środek nowego otoczenia<br><math>x^{(k+1)}=x^{\mathrm{M}(k)}=\alpha (x^{\mathrm{M}(k)}-x^{(k)})+x^{(k)}, \alpha=1</math>, | ||
a następnie przeszukiwać je tak jak poprzednio. | a następnie przeszukiwać je tak jak poprzednio. | ||
| Linia 53: | Linia 53: | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd8.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd8.png|thumb|500px]] | ||
|valign="top"|Algorytm może być też: | |valign="top"|Algorytm może być też: | ||
*'''odważny''' (wiem, że schody opadają w prawo, skaczę kilka stopni w prawo) i przesunąć środek kuli poszukiwań wzdłuż kierunku wyznaczonego przez różnicę wektorów <math>x^{M(k)}-x^{k}=d</math> , tzn. ustalić środek nowej kuli w punkcie<br><math>x^{M(k)}=\alpha (x^{M(k)}-x^(k))+x^{(k)}, \alpha>1</math>. | *'''odważny''' (wiem, że schody opadają w prawo, skaczę kilka stopni w prawo) i przesunąć środek kuli poszukiwań wzdłuż kierunku wyznaczonego przez różnicę wektorów <math>x^{\mathrm{M}(k)}-x^{(k)}=d</math> , tzn. ustalić środek nowej kuli w punkcie<br><math>x^{\mathrm{M}(k)}=\alpha (x^{\mathrm{M}(k)}-x^{(k)})+x^{(k)}, \alpha>1</math>. | ||
|} | |} | ||
---- | ---- | ||
| Linia 93: | Linia 93: | ||
{| border="0" cellpadding="4" width="125%" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd14.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd14.png|thumb|500px]] | ||
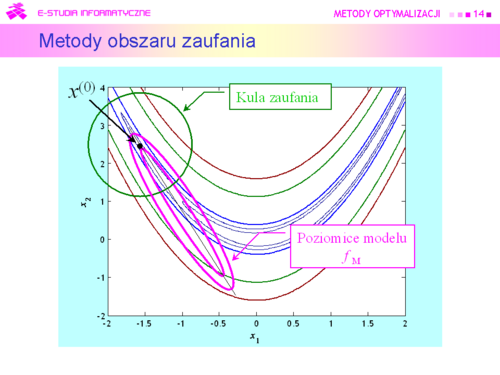
|valign="top"|Przyjmujemy zatem, że dookoła punktu bieżącego <math>x^{(k)}</math> została określona kula <math>\mathbb{K}\ (x, r)</math> i '''funkcja''' <math>\boldsymbol{x \mapsto f_M(x)}</math> '''będąca modelem zachowania się funkcji wyboru''' <math>\boldsymbol{f}</math> '''w tej kuli''', modelem dużo prostszym w analizie niż funkcja oryginalna. Do określenia modelu możemy posłużyć się intuicją opartą na rozważaniach punktu drugiego, co jak pamiętamy przekłada się na przeświadczenie, że funkcja celu dobrze daje się przybliżyć funkcją kwadratową<center><math>x \mapsto x^TQx+c^Tx+\sigma</math> | |valign="top"|Przyjmujemy zatem, że dookoła punktu bieżącego <math>x^{(k)}</math> została określona kula <math>\mathbb{K}\ (x, r)</math> i '''funkcja''' <math>\boldsymbol{x \mapsto f_M(x)}</math> '''będąca modelem zachowania się funkcji wyboru''' <math>\boldsymbol{f}</math> '''w tej kuli''', modelem dużo prostszym w analizie niż funkcja oryginalna. Do określenia modelu możemy posłużyć się intuicją opartą na rozważaniach punktu drugiego, co jak pamiętamy przekłada się na przeświadczenie, że funkcja celu dobrze daje się przybliżyć funkcją kwadratową<center><math>x \mapsto x^TQx+c^Tx+\sigma \quad</math> '''(APR)'''</center> | ||
|} | |} | ||
---- | ---- | ||
| Linia 99: | Linia 99: | ||
{| border="0" cellpadding="4" width="125%" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd15.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd15.png|thumb|500px]] | ||
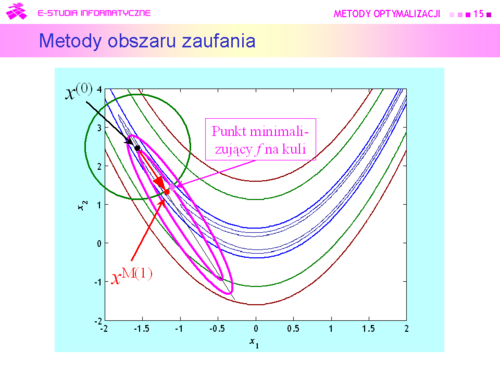
|valign="top"|W takiej sytuacji przeszukanie otoczenia może oznaczać tylko jedno — '''szukanie punktu''' <math>x^{M(k)}</math>, '''minimalizującego funkcję modelującą na kuli'''.<br>Punkt ten oczywiście będzie się '''różnił''' od rzeczywistego minimum funkcji celu <math>f</math> na kuli zaufania, ale mamy nadzieję, że '''niewiele''', a co ważniejsze będzie spełniona nierówność<center><math>f(x^{M(k)})<f(x^{k-1})</math></center>oznaczająca, że funkcja celu z kroku na krok maleje. | |valign="top"|W takiej sytuacji przeszukanie otoczenia może oznaczać tylko jedno — '''szukanie punktu''' <math>x^{\mathrm{M}(k)}</math>, '''minimalizującego funkcję modelującą na kuli'''.<br>Punkt ten oczywiście będzie się '''różnił''' od rzeczywistego minimum funkcji celu <math>f</math> na kuli zaufania, ale mamy nadzieję, że '''niewiele''', a co ważniejsze będzie spełniona nierówność<center><math>f(x^{\mathrm{M}(k)})<f(x^{k-1})</math></center>oznaczająca, że funkcja celu z kroku na krok maleje. | ||
|} | |} | ||
| Linia 106: | Linia 106: | ||
{| border="0" cellpadding="4" width="125%" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd16.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd16.png|thumb|500px]] | ||
|valign="top"|Ponieważ punkt <math>x^{M(k)}</math> został wygenerowany w oparciu o model, to gdy kula jest za duża, może nie być właściwy — wartość funkcji celu może być w nim większa niż w punkcie centralnym kuli. Oznacza to, że w stosowny sposób '''trzeba dostosowywać promień kuli''' do zmienności funkcji celu. Zauważmy też, że przy takim podejściu, aby znaleźć rozwiązanie zadania optymalizacji bez ograniczeń trzeba rozwiązywać wielokrotnie zadanie z ograniczeniami ale z prostą funkcją wyboru — kwadratową funkcją aproksymującą. | |valign="top"|Ponieważ punkt <math>x^{\mathrm{M}(k)}</math> został wygenerowany w oparciu o model, to gdy kula jest za duża, może nie być właściwy — wartość funkcji celu może być w nim większa niż w punkcie centralnym kuli. Oznacza to, że w stosowny sposób '''trzeba dostosowywać promień kuli''' do zmienności funkcji celu. Zauważmy też, że przy takim podejściu, aby znaleźć rozwiązanie zadania optymalizacji bez ograniczeń trzeba rozwiązywać wielokrotnie zadanie z ograniczeniami ale z prostą funkcją wyboru — kwadratową funkcją aproksymującą. | ||
|} | |} | ||
---- | ---- | ||
| Linia 112: | Linia 112: | ||
{| border="0" cellpadding="4" width="125%" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd17.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd17.png|thumb|500px]] | ||
|valign="top"|W świetle ostatniej uwagi jest oczywiste, że algorytmy wykorzystujące omawiane podejście mogły liczyć na sukces dopiero w momencie, kiedy opracowano efektywne algorytmy rozwiązywania występujących w nich zadań<center><math>f_M(x)=x^ | |valign="top"|W świetle ostatniej uwagi jest oczywiste, że algorytmy wykorzystujące omawiane podejście mogły liczyć na sukces dopiero w momencie, kiedy opracowano efektywne algorytmy rozwiązywania występujących w nich zadań<center><math>f_M(x)=x^{\mathrm T}Qx+c^{\mathrmT}x+\sigma \rightarrow </math> min <br> p.o. <math>(x-x^{(k)})^{\mathrm{T}}(x-x^{(k)})\le r^2</math>,</center> co nastąpiło w połowie lat siedemdziesiątych ubiegłego wieku. | ||
|} | |} | ||
---- | ---- | ||
| Linia 127: | Linia 127: | ||
<u>Kroki algorytmu</u> | <u>Kroki algorytmu</u> | ||
#Dla punktu <math>x^{(k)}</math> wyznacz model <math>f_M(\cdot; x^{(k)})</math> funkcji celu w jego otoczeniu. | #Dla punktu <math>x^{(k)}</math> wyznacz model <math>f_M(\cdot; x^{(k)})</math> funkcji celu w jego otoczeniu. | ||
#Znajdź przybliżenie <math>\tilde{x}^{(k)}</math> punktu <br><math>x^{M(k)}</math> = arg min<math>_{x\epsilon T(x^{(k)})}f_M(x;x^{(k)})</math>. | #Znajdź przybliżenie <math>\tilde{x}^{(k)}</math> punktu <br><math>x^{\mathrm{M}(k)}</math> = arg min<math>_{x\epsilon T(x^{(k)})}f_M(x;x^{(k)})</math>. | ||
#Sprawdź czy wielkość obszaru zaufania została wybrana właściwie. Jeżeli tak, podstaw <math>x^{(k)} :=\tilde x^{(k)}</math> , idź do 5. W przeciwnym przypadku idź do 4. | #Sprawdź czy wielkość obszaru zaufania została wybrana właściwie. Jeżeli tak, podstaw <math>x^{(k)} :=\tilde x^{(k)}</math> , idź do 5. W przeciwnym przypadku idź do 4. | ||
#Zmniejsz obszar zaufania do <math>TS</math>, podstaw <math>T(x^{(k)}) := TS</math>, idź do 2. | #Zmniejsz obszar zaufania do <math>TS</math>, podstaw <math>T(x^{(k)}) := TS</math>, idź do 2. | ||
| Linia 179: | Linia 179: | ||
{| border="0" cellpadding="4" width="125%" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd25.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd25.png|thumb|500px]] | ||
|valign="top"|Zgodnie z określeniem poruszania się wzdłuż kierunku, znalezienie punktu <math>\bar{x} \in P(x^{(k)};d)\subset \mathbb{R}^n</math> jest równoważne ustaleniu pewnego <math>\bar{\alpha} \in \mathbb{R}</math>. Zatem '''zmieniając''' <math>\alpha</math> '''od zera do plus nieskończoności''' ruszamy się wzdłuż prostej <math>P(x^{(k)};d)</math> w kierunku malenia funkcji celu. Konkretną wartość <math>\bar{\alpha}</math> – '''długość kroku''' – możemy ustalić ''a priori''. Intuicyjnie nie jest to najlepszy sposób, bo żeby zabezpieczyć się przed zbytnim przeskoczeniem minimum funkcji celu na zbiorze <math>P(x^{(k)};d)</math> trzeba tą stałą długość kroku wybrać niewielką. Wobec tego można postępować tak:<br> | |valign="top"|Zgodnie z określeniem poruszania się wzdłuż kierunku, znalezienie punktu <math>\bar{x} \in \mathrm P(x^{(k)};d)\subset \mathbb{R}^n</math> jest równoważne ustaleniu pewnego <math>\bar{\alpha} \in \mathbb{R}</math>. Zatem '''zmieniając''' <math>\alpha</math> '''od zera do plus nieskończoności''' ruszamy się wzdłuż prostej <math>\mathrm P(x^{(k)};d)</math> w kierunku malenia funkcji celu. Konkretną wartość <math>\bar{\alpha}</math> – '''długość kroku''' – możemy ustalić ''a priori''. Intuicyjnie nie jest to najlepszy sposób, bo żeby zabezpieczyć się przed zbytnim przeskoczeniem minimum funkcji celu na zbiorze <math>\mathrm P(x^{(k)};d)</math> trzeba tą stałą długość kroku wybrać niewielką. Wobec tego można postępować tak:<br> | ||
wybieramy duży krok początkowy <math>\alpha ^{(0)}</math>,<br> | wybieramy duży krok początkowy <math>\alpha ^{(0)}</math>,<br> | ||
gdy <math>f(x^{(k)}+\alpha ^{(0)}d)<f(x^{(k)})</math> to <math>\alpha^{(0)}</math> uznajemy za długość kroku,<br>gdy przeciwnie – zmniejszamy <math>\alpha^{(0)}</math> do <math>\alpha^{(1)}</math>),<br>powtarzamy sprawdzenie czy wartość funkcji zmalała, itd. aż uzyskamy krok dający poprawę. | gdy <math>f(x^{(k)}+\alpha ^{(0)}d)<f(x^{(k)})</math> to <math>\alpha^{(0)}</math> uznajemy za długość kroku,<br>gdy przeciwnie – zmniejszamy <math>\alpha^{(0)}</math> do <math>\alpha^{(1)}</math>),<br>powtarzamy sprawdzenie czy wartość funkcji zmalała, itd. aż uzyskamy krok dający poprawę. | ||
| Linia 187: | Linia 187: | ||
{| border="0" cellpadding="4" width="125%" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd26.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd26.png|thumb|500px]] | ||
|valign="top"|Dokonujemy, jak mówimy '''minimalizacji w kierunku'''. Formułując to zadanie przybliżonej minimalizacji funkcji jednej zmiennej <math>\alpha</math> (<math>x^{(k)}</math> i <math>d</math> są ustalone!) wykorzystaliśmy fakt, że zbiór dopuszczalny <math>P(x^{(k)};d)</math> jest określony jednym ograniczeniem równościowym. | |valign="top"|Dokonujemy, jak mówimy '''minimalizacji w kierunku'''. Formułując to zadanie przybliżonej minimalizacji funkcji jednej zmiennej <math>\alpha</math> (<math>x^{(k)}</math> i <math>d</math> są ustalone!) wykorzystaliśmy fakt, że zbiór dopuszczalny <math>\mathrm P(x^{(k)};d)</math> jest określony jednym ograniczeniem równościowym. | ||
Wprawdzie wiemy, że „ruszanie się” wzdłuż kierunku poprawy nie musi doprowadzić do minimum globalnego, ale na pewno poprawi wartość funkcji celu. O ile poprawi ? – Może poprawić bardzo niewiele, ale tak jak przy ustalaniu podstaw poprzednich metod, zgodnie z naszym podejściem optymistycznym, uważamy że ta poprawa będzie istotna. Jak pamiętamy przekonanie to ma podstawy formalne, ponieważ rozważania teoretyczne sugerują, że „porządne” funkcje są lokalnie wypukłe, a co za tym idzie nie powinno być kłopotów ze znalezieniem punktu lepszego niż bieżący. Przy wymyślaniu kryterium stopu pomocny może być warunek stacjonarności gradientu wskazujący na możliwość konstrukcji kryterium stopu w oparciu o jakąś miarę „małości” gradientu. | Wprawdzie wiemy, że „ruszanie się” wzdłuż kierunku poprawy nie musi doprowadzić do minimum globalnego, ale na pewno poprawi wartość funkcji celu. O ile poprawi ? – Może poprawić bardzo niewiele, ale tak jak przy ustalaniu podstaw poprzednich metod, zgodnie z naszym podejściem optymistycznym, uważamy że ta poprawa będzie istotna. Jak pamiętamy przekonanie to ma podstawy formalne, ponieważ rozważania teoretyczne sugerują, że „porządne” funkcje są lokalnie wypukłe, a co za tym idzie nie powinno być kłopotów ze znalezieniem punktu lepszego niż bieżący. Przy wymyślaniu kryterium stopu pomocny może być warunek stacjonarności gradientu wskazujący na możliwość konstrukcji kryterium stopu w oparciu o jakąś miarę „małości” gradientu. | ||
Wersja z 13:17, 10 paź 2006
 |
 |
 |
 |
 |
Algorytm może być:
a następnie przeszukiwać je tak jak poprzednio. |
 |
 |
Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm wymyślony przez:
|
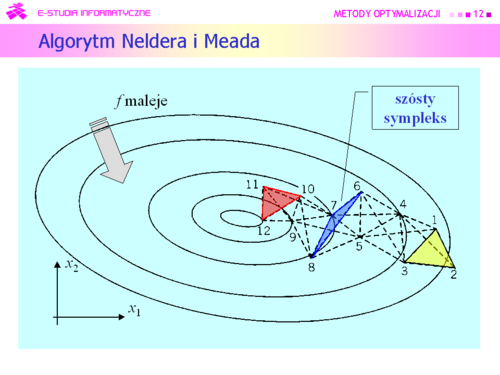 |
Dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo ładnie. |
 |
Metody oparte na takim rozumowaniu od połowy lat dziewięćdziesiątych XX w nazywa się:
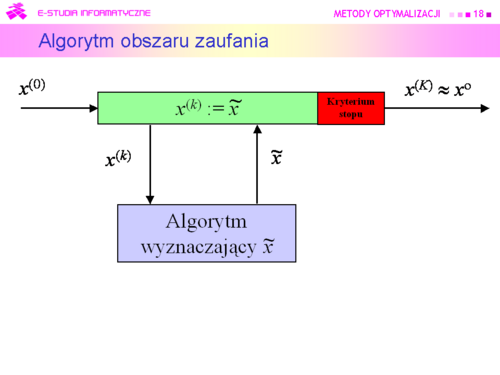
(Trust region methods) |
 |
 |
 |
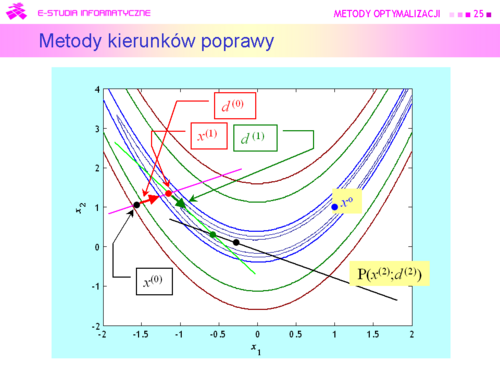
Tu oczywistym pomysłem jest wykorzystanie rozważań teoretycznych, pokazujących związek kierunku poprawy z gradientem (lemat 4.3).
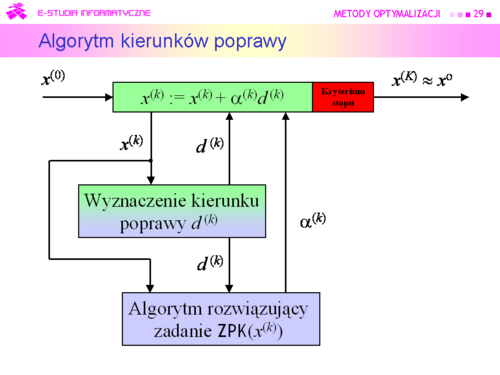
Algorytm będzie zatem wykorzystywał: |
 |
 |
 |
 |
Teraz zauważmy tylko, że test stopu powinien zawierać dwa warunki: jeden badający “optymalność” kolejnego punktu, a drugi określający maksymalną liczbę iteracji. |
 |
 |
 |
 |
 |
 |