MO Moduł 3: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 11: | Linia 11: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M3_Slajd3.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M3_Slajd3.png|thumb|500px]] | ||
|valign="top"|Funkcja oceny jest tu liniowa, bo jest oczywiste, że dodanie do niej dowolnej liczby nie zmienia rozważań (zmienia wartość funkcji wyboru w punkcie minimalizującym, która jest oczywiście od tej liczby zależna, ale rozwiązaniem zadania jest punkt minimalizujący, który jest taki sam !). | |valign="top"|Funkcja oceny jest tu liniowa, bo jest oczywiste, że dodanie do niej dowolnej liczby nie zmienia rozważań (zmienia wartość funkcji wyboru w punkcie minimalizującym, która jest oczywiście od tej liczby zależna, ale <u>rozwiązaniem zadania jest punkt minimalizujący</u>, który jest taki sam !). | ||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M3_Slajd4.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M3_Slajd4.png|thumb|500px]] | ||
|valign="top"|Zamiast „przy ograniczeniach” będziemy pisali | |valign="top"|Zamiast „przy ograniczeniach” będziemy pisali <math>\;\;\mathrm {p.o.}</math> | ||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M3_Slajd5.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M3_Slajd5.png|thumb|500px]] | ||
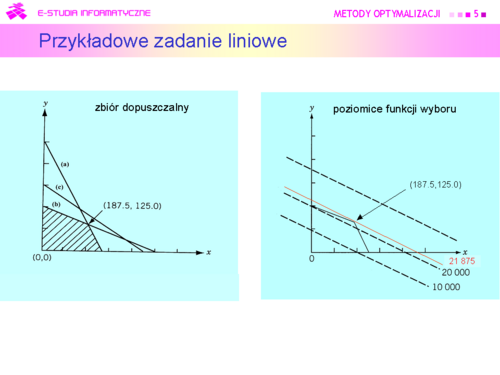
|valign="top"|Z rysunku wynika, że ograniczenie (c) nie jest potrzebne, oraz że zbiór dopuszczalny jest wielokątem. Linie poziomicowe funkcji liniowej to proste, zatem rozwiązanie leży w wierzchołku wielokąta (albo rozwiązań jest wiele i leżą na brzegu wielokąta, gdy poziomice są równoległe do stosownego ograniczenia). | |valign="top"|Z rysunku wynika, że ograniczenie (c) nie jest potrzebne, oraz że zbiór dopuszczalny jest wielokątem. Linie poziomicowe funkcji liniowej to proste, zatem rozwiązanie leży w wierzchołku wielokąta (albo rozwiązań jest wiele i leżą na brzegu wielokąta, gdy poziomice są równoległe do stosownego ograniczenia). | ||
| Linia 29: | Linia 29: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M3_Slajd6.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M3_Slajd6.png|thumb|500px]] | ||
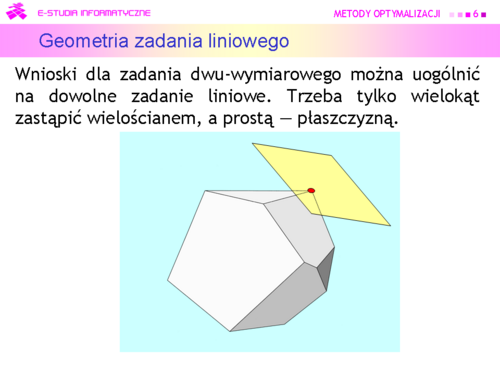
|valign="top"|W przestrzeni zmiennych zadania liniowego optymalizacji | |valign="top"|W przestrzeni zmiennych zadania liniowego optymalizacji | ||
*'''zbiór dopuszczalny to (hiper)wielościan''', | |||
*zbiór dopuszczalny to (hiper)wielościan, | *miejscem geometrycznym '''stałej wartości funkcji celu jest (hiper)-płaszczyzna''', a | ||
*miejscem geometrycznym stałej wartości funkcji celu jest (hiper)-płaszczyzna, a | *'''rozwiązanie zadania''' (o ile istnieje) '''leży w jego wierzchołku''' albo rozwiązań jest wiele i leżą na brzegu wielościanu albo na jego ścianie. | ||
*rozwiązanie zadania (o ile istnieje) leży w jego wierzchołku albo rozwiązań jest wiele i leżą na brzegu wielościanu albo na jego ścianie | |||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M3_Slajd7.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M3_Slajd7.png|thumb|500px]] | ||
|valign="top"|Na płaszczyźnie taki algorytm będzie działać, bo każdy wierzchołek ma tylko dwu sąsiadów, ale przy większej liczbie wymiarów będzie to bardzo powolne i nie wiadomo, czy algorytm się nie zapętli. | |valign="top"|Na płaszczyźnie taki algorytm będzie działać, bo każdy wierzchołek ma tylko dwu sąsiadów, ale przy większej liczbie wymiarów będzie to bardzo powolne i nie wiadomo, czy algorytm się nie zapętli. | ||
| Linia 46: | Linia 45: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M3_Slajd8.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M3_Slajd8.png|thumb|500px]] | ||
|valign="top"|W Polsce, nie bardzo wiadomo dlaczego, algorytm Dantziga nazywa się metodą sympleks, simpleksową, a nawet metodą sympleksów. | |valign="top"|W Polsce, nie bardzo wiadomo dlaczego, algorytm Dantziga nazywa się metodą sympleks, simpleksową, a nawet metodą sympleksów. | ||
| Linia 90: | Linia 89: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M3_Slajd15.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M3_Slajd15.png|thumb|500px]] | ||
|valign="top"|Dla równania | |valign="top"|Dla równania<center><math>Ax = b,</math></center> gdzie <math>x</math> jest wektorem <math>n</math> wymiarowym, a <math>b</math> wektorem <math>p</math> wymiarowym, '''macierzą bazową''' nazywa się każdą kwadratową <u>nieosobliwą</u> macierz <math>B</math>, którą da się utworzyć z <math>p</math> kolumn macierzy <math>A</math>. | ||
<math>Ax = b,</math> | |||
gdzie x jest wektorem n wymiarowym, a b wektorem p wymiarowym, macierzą bazową nazywa się każdą kwadratową nieosobliwą macierz B, którą da się utworzyć z p kolumn macierzy A. | |||
|} | |} | ||
| Linia 156: | Linia 150: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M3_Slajd25.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M3_Slajd25.png|thumb|500px]] | ||
|valign="top"|Główne problemy implementacyjne związane są z szybkością i dokładnością tego algorytmu. Najwięcej kłopotów jest w nim z odwracaniem kolejnych macierzy bazowych. Przypominamy, że numerycznie macierz odwraca się drogą faktoryzacji. | |valign="top"|Główne problemy implementacyjne związane są z szybkością i dokładnością tego algorytmu. Najwięcej kłopotów jest w nim z odwracaniem kolejnych macierzy bazowych. Przypominamy, że numerycznie macierz odwraca się drogą faktoryzacji. | ||
| Linia 162: | Linia 156: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M3_Slajd26.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M3_Slajd26.png|thumb|500px]] | ||
|valign="top"|Uznane pakiety komercyjne zawierające algorytm Simplex to np. CPLEX, MINOS, NAG, AMPL, MATLAB i Mathematica | |valign="top"|Uznane pakiety komercyjne zawierające algorytm Simplex to np. CPLEX, MINOS, NAG, AMPL, MATLAB i Mathematica | ||
Wersja z 12:01, 10 paź 2006
 |
 |
 |
Zamiast „przy ograniczeniach” będziemy pisali |
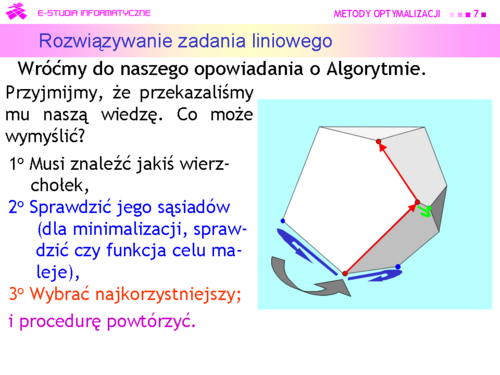 |
Na płaszczyźnie taki algorytm będzie działać, bo każdy wierzchołek ma tylko dwu sąsiadów, ale przy większej liczbie wymiarów będzie to bardzo powolne i nie wiadomo, czy algorytm się nie zapętli. |
 |
 |
 |
 |
 |
 |
 |
Dla równania |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Uznane pakiety komercyjne zawierające algorytm Simplex to np. CPLEX, MINOS, NAG, AMPL, MATLAB i Mathematica |
 |
 |
 |
 |
 |
 |
 |