MO Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 11: | Linia 11: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd3.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd3.png|thumb|500px]] | ||
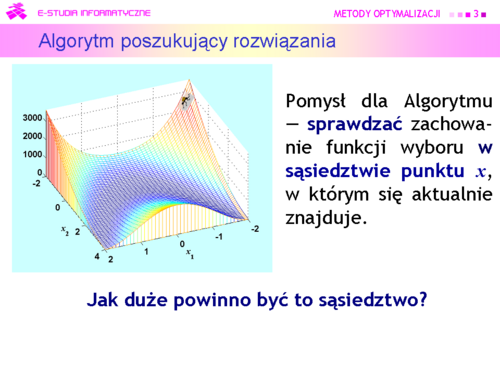
|valign="top"|Powróćmy do naszych rozważań z części drugiej wykładu trzeciego. | |valign="top"|Powróćmy do naszych rozważań z części drugiej wykładu trzeciego. | ||
Jak pamiętamy, Algorytm jest ślepy — nie może zobaczyć rzeźby trenu na którym się znajduje. | Jak pamiętamy, Algorytm jest ślepy — nie może zobaczyć rzeźby trenu na którym się znajduje. | ||
Na schodach szedł w prawo, potem w lewo — sprawdzał swoje otoczenie. Teraz otoczenie ma więcej wymiarów, ale pomysł może być ten sam — sprawdzać zachowanie funkcji wyboru w sąsiedztwie punktu <math>x</math>, w którym się aktualnie znajduje. | Na schodach szedł w prawo, potem w lewo — sprawdzał swoje otoczenie. Teraz otoczenie ma więcej wymiarów, ale pomysł może być ten sam — '''sprawdzać''' zachowanie funkcji wyboru w sąsiedztwie punktu <math>x</math>, w którym się aktualnie znajduje. | ||
Natychmiast pojawia się pytanie — jak duże powinno być to sąsiedztwo? | Natychmiast pojawia się pytanie — '''jak duże powinno być to sąsiedztwo?''' | ||
Udzielenie przemyślanej odpowiedzi nie jest zagadnieniem łatwym, ponieważ wielkość przeszukiwanego obszaru ma, intuicyjnie, wpływ, z jednej strony na szybkość znalezienia ekstremum mierzoną ilością sprawdzanych obszarów (im większy tym szybciej), a z drugiej na dokładność Algorytmu (przy ograniczonych możliwościach przeszukiwania — im mniejszy tym dokładniej). | Udzielenie przemyślanej odpowiedzi nie jest zagadnieniem łatwym, ponieważ wielkość przeszukiwanego obszaru ma, intuicyjnie, wpływ, z jednej strony na szybkość znalezienia ekstremum mierzoną ilością sprawdzanych obszarów (im większy tym szybciej), a z drugiej na dokładność Algorytmu (przy ograniczonych możliwościach przeszukiwania — im mniejszy tym dokładniej). | ||
| Linia 34: | Linia 34: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd6.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd6.png|thumb|500px]] | ||
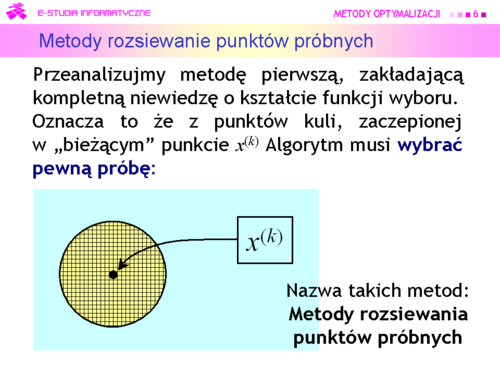
|valign="top"|Przeanalizujmy teraz sposób pierwszy, zakładający kompletną niewiedzę o kształcie funkcji wyboru. Oznacza to że z punktów kuli, zaczepionej w „bieżącym” punkcie <math>x^{(k)}</math> Algorytm musi wybrać pewną próbę, np. tworząc wielowymiarową siatkę i jej węzły uznać za próbę (podejście deterministyczne), czy też wygenerować próbę losowo, bacząc aby była rozłożona równomiernie (podejście probabilistyczne). | |valign="top"|Przeanalizujmy teraz sposób pierwszy, zakładający kompletną niewiedzę o kształcie funkcji wyboru. Oznacza to że z punktów kuli, zaczepionej w „bieżącym” punkcie <math>x^{(k)}</math> Algorytm musi '''wybrać pewną próbę''', np. tworząc wielowymiarową siatkę i jej węzły uznać za próbę (''podejście deterministyczne''), czy też wygenerować próbę losowo, bacząc aby była rozłożona równomiernie (''podejście probabilistyczne''). | ||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd7.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd7.png|thumb|500px]] | ||
|valign="top"|Algorytm może być: | |valign="top"|Algorytm może być: | ||
*'''ostrożny''' (wiem, że schody opadają w prawo, schodzę w prawo jeden stopień) i przyjąć <math>x^{M(k)}</math> za środek nowego otoczenia | *'''ostrożny''' (wiem, że schody opadają w prawo, schodzę w prawo jeden stopień) i przyjąć <math>x^{M(k)}</math> za środek nowego otoczenia | ||
<math>x^{(k+1)}=x^{M(k)}=\alpha (x^{M(k)}-x^{(k)})+x^{(k)}, \alpha=1</math> | <math>x^{(k+1)}=x^{M(k)}=\alpha (x^{M(k)}-x^{(k)})+x^{(k)}, \alpha=1</math> | ||
a następnie przeszukiwać je tak jak poprzednio. | a następnie przeszukiwać je tak jak poprzednio. | ||
| Linia 51: | Linia 52: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd8.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd8.png|thumb|500px]] | ||
|valign="top"|Algorytm może być też: | |valign="top"|Algorytm może być też: | ||
*'''odważny''' (wiem, że schody opadają w prawo, skaczę kilka stopni w prawo) i przesunąć środek kuli poszukiwań wzdłuż kierunku wyznaczonego przez różnicę wektorów <math>x^{M(k)}-x^{k}=d</math> , tzn. ustalić środek nowej kuli w punkcie | *'''odważny''' (wiem, że schody opadają w prawo, skaczę kilka stopni w prawo) i przesunąć środek kuli poszukiwań wzdłuż kierunku wyznaczonego przez różnicę wektorów <math>x^{M(k)}-x^{k}=d</math> , tzn. ustalić środek nowej kuli w punkcie | ||
<math>x^{M(k)}=\alpha (x^{M(k)}-x^(k))+x^{(k)}, \alpha>1</math> | <math>x^{M(k)}=\alpha (x^{M(k)}-x^(k))+x^{(k)}, \alpha>1</math>. | ||
|} | |} | ||
---- | ---- | ||
| Linia 65: | Linia 66: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd10.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd10.png|thumb|500px]] | ||
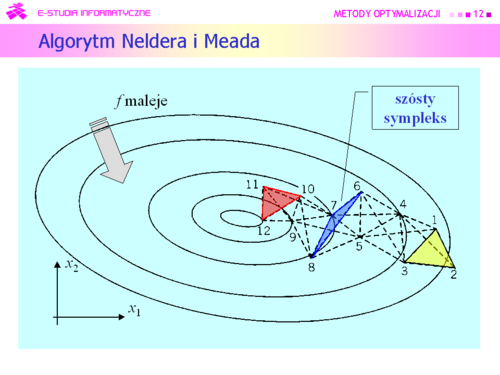
|valign="top"|Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm wymyślony przez: | |valign="top"|Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm wymyślony przez: | ||
| Linia 73: | Linia 74: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd11.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd11.png|thumb|500px]] | ||
|valign="top"|Nie będziemy zagłębiali się w szczegóły algorytmu Neldera i Meada (jak ustalić próbę początkową, jak będąc odważnym zachować niezbędny stopień ostrożności itd.) odsyłając Czytelnika np. do monografii A. Stachurski, A. Wierzbicki: Podstawy optymalizacji, Oficyna Wydawnicza PW 1999, rozdział 3.10. | |valign="top"|Nie będziemy zagłębiali się w szczegóły algorytmu Neldera i Meada (jak ustalić próbę początkową, jak będąc odważnym zachować niezbędny stopień ostrożności itd.) odsyłając Czytelnika np. do monografii A. Stachurski, A. Wierzbicki: ''Podstawy optymalizacji'', Oficyna Wydawnicza PW 1999, rozdział 3.10. | ||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd12.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd12.png|thumb|500px]] | ||
|valign="top"|Dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo ładnie. | |valign="top"|Dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo ładnie. | ||
| Linia 85: | Linia 86: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd13.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd13.png|thumb|500px]] | ||
|valign="top"|Metody oparte na takim rozumowaniu od połowy lat dziewięćdziesiątych XX w nazywa się: | |valign="top"|Metody oparte na takim rozumowaniu od połowy lat dziewięćdziesiątych XX w nazywa się: | ||
'''Metodami obszaru zaufania | '''Metodami obszaru zaufania''' | ||
(Trust region methods)''' | |||
'''(Trust region methods)''' | |||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd14.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd14.png|thumb|500px]] | ||
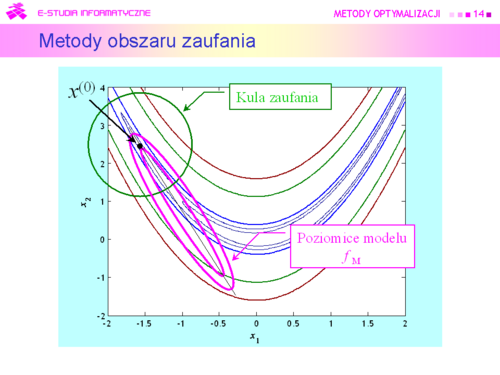
|valign="top"|Przyjmujemy zatem, że dookoła punktu bieżącego <math>x^{(k)}</math> została określona kula <math>\mathbb{K}\ (x, r)</math> i funkcja <math>x \mapsto f_M(x)</math> | |valign="top"|Przyjmujemy zatem, że dookoła punktu bieżącego <math>x^{(k)}</math> została określona kula <math>\mathbb{K}\ (x, r)</math> i '''funkcja''' <math>x \mapsto f_M(x)</math> '''będąca modelem zachowania się funkcji wyboru''' <math>f</math> '''w tej kuli''', modelem dużo prostszym w analizie niż funkcja oryginalna. Do określenia modelu możemy posłużyć się intuicją opartą na rozważaniach punktu drugiego, co jak pamiętamy przekłada się na przeświadczenie, że funkcja celu dobrze daje się przybliżyć funkcją kwadratową | ||
<math> | <math>x \mapsto x^TQx+c^Tx+\sigma</math> '''(APR)''' | ||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd15.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd15.png|thumb|500px]] | ||
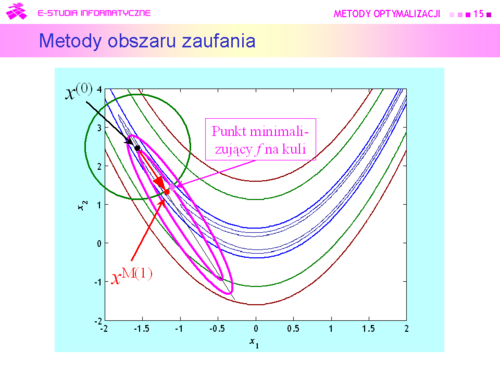
|valign="top"|W takiej sytuacji przeszukanie otoczenia może oznaczać tylko jedno | |valign="top"|W takiej sytuacji przeszukanie otoczenia może oznaczać tylko jedno — '''szukanie punktu''' <math>x^{M(k)}</math>, '''minimalizującego funkcję modelującą na kuli'''. | ||
Punkt ten oczywiście będzie się różnił od rzeczywistego minimum funkcji celu f na kuli zaufania, ale mamy nadzieję, że niewiele, a co ważniejsze będzie spełniona nierówność | Punkt ten oczywiście będzie się '''różnił''' od rzeczywistego minimum funkcji celu <math>f</math> na kuli zaufania, ale mamy nadzieję, że '''niewiele''', a co ważniejsze będzie spełniona nierówność | ||
<math>f(x^{M(k)})<f(x^{k-1})</math> | |||
<math>f(x^{M(k)}<f(x^{k-1})</math> | |||
oznaczająca, że funkcja celu z kroku na krok maleje. | oznaczająca, że funkcja celu z kroku na krok maleje. | ||
| Linia 114: | Linia 114: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd16.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd16.png|thumb|500px]] | ||
|valign="top"|Ponieważ punkt<math> x^{M(k)}</math> został wygenerowany w oparciu o model, to gdy kula jest za duża, może nie być właściwy | |valign="top"|Ponieważ punkt <math>x^{M(k)}</math> został wygenerowany w oparciu o model, to gdy kula jest za duża, może nie być właściwy — wartość funkcji celu może być w nim większa niż w punkcie centralnym kuli. Oznacza to, że w stosowny sposób '''trzeba dostosowywać promień kuli''' do zmienności funkcji celu. Zauważmy też, że przy takim podejściu, aby znaleźć rozwiązanie zadania optymalizacji bez ograniczeń trzeba rozwiązywać wielokrotnie zadanie z ograniczeniami ale z prostą funkcją wyboru — kwadratową funkcją aproksymującą. | ||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd17.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd17.png|thumb|500px]] | ||
|valign="top"|W świetle ostatniej uwagi jest oczywiste, że algorytmy wykorzystujące omawiane podejście mogły liczyć na sukces dopiero w momencie, kiedy opracowano efektywne algorytmy rozwiązywania występujących w nich zadań | |valign="top"|W świetle ostatniej uwagi jest oczywiste, że algorytmy wykorzystujące omawiane podejście mogły liczyć na sukces dopiero w momencie, kiedy opracowano efektywne algorytmy rozwiązywania występujących w nich zadań | ||
<math>f_M(x)=x^TQx+c^Tx+\sigma \rightarrow </math> min | |||
<math> | p.o. <math>(x-x^{(k)})^T(x-x^(k))\le r^2</math>, | ||
co nastąpiło w połowie lat siedemdziesiątych ubiegłego wieku. | |||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd18.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd18.png|thumb|500px]] | ||
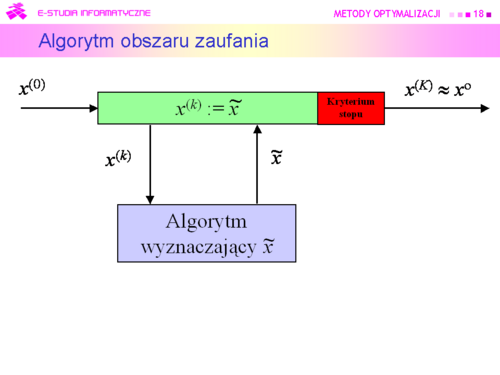
|valign="top"|'''Podstawowy algorytm obszaru zaufania''' | |valign="top"|'''Podstawowy algorytm obszaru zaufania''' | ||
| Linia 137: | Linia 138: | ||
Inicjalizacja | Inicjalizacja | ||
Wybierz punkt początkowy <math>x^{(0)}</math>. | Wybierz punkt początkowy <math>x^{(0)}</math>. | ||
Ustal początkowy obszar zaufania <math>T(x^{(0)}</math> | Ustal początkowy obszar zaufania <math>T(x^{(0)})</math>. | ||
Podstaw k := 0. | Podstaw <math>k := 0</math>. | ||
Kroki algorytmu | Kroki algorytmu | ||
#Dla punktu <math>x^{(k)}</math> wyznacz model <math>f_M(\cdot; x^{(k)})</math> funkcji celu w jego otoczeniu. | #Dla punktu <math>x^{(k)}</math> wyznacz model <math>f_M(\cdot; x^{(k)})</math> funkcji celu w jego otoczeniu. | ||
#Znajdź przybliżenie | #Znajdź przybliżenie <math>\tilde{x}^{(k)}</math> punktu | ||
#Sprawdź czy wielkość obszaru zaufania została wybrana właściwie. Jeżeli tak, podstaw <math> | <math>x^{M(k)}</math> = arg min<math>_{x\epsilon T(x^{(k)})}f_M(x;x^{(k)})</math>. | ||
#Zmniejsz obszar zaufania do TS, podstaw <math>T(x^{(k)}) := TS</math>, idź do 2. | #Sprawdź czy wielkość obszaru zaufania została wybrana właściwie. Jeżeli tak, podstaw <math>x^{(k)} :=\tilde x^{(k)}</math> , idź do 5. W przeciwnym przypadku idź do 4. | ||
#Zmniejsz obszar zaufania do <math>TS</math>, podstaw <math>T(x^{(k)}) := TS</math>, idź do 2. | |||
#Jeżeli spełnione jest kryterium stopu, to <math>x^{(k)}</math> przyjmij za rozwiązanie i stop. W przeciwnym przypadku idź do 6. | #Jeżeli spełnione jest kryterium stopu, to <math>x^{(k)}</math> przyjmij za rozwiązanie i stop. W przeciwnym przypadku idź do 6. | ||
#Sprawdź czy należy powiększyć obszar zaufania do TL. Jeżeli tak, podstaw <math>T(x^{(k)}) := TL</math>, idź do 7. W przeciwnym przypadku idź do 7. | #Sprawdź czy należy powiększyć obszar zaufania do <math>TL</math>. Jeżeli tak, podstaw <math>T(x^{(k)}) := TL</math>, idź do 7. W przeciwnym przypadku idź do 7. | ||
#Podstaw k := k + 1, idź do 1. | #Podstaw <math>k := k + 1</math>, idź do 1. | ||
Wyjaśnień wymagają kroki 2, 3, 6 i oczywiście kryterium stopu. | Wyjaśnień wymagają kroki '''2, 3, 6''' i oczywiście '''kryterium stopu'''. | ||
|} | |} | ||
| Linia 166: | Linia 168: | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd21.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd21.png|thumb|500px]] | ||
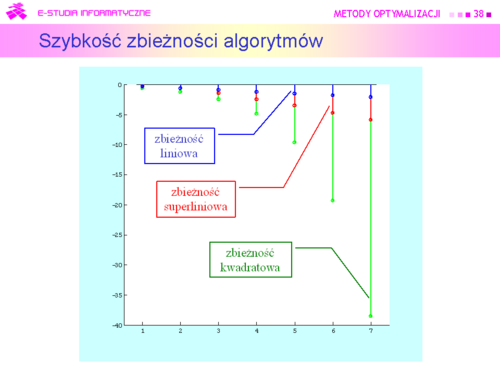
|valign="top"|Ciąg prostszych zadań daje ciąg rozwiązań <math> | |valign="top"|Ciąg prostszych zadań daje ciąg rozwiązań {<math> x^{(k)}</math>}<math>_{k = 0}^\infty}</math> Naturalne pytanie które postawiliśmy, to kiedy go uciąć – '''które <math>k</math> uznać za ostatnie''', dające rozwiązanie z dostateczną dokładnością. Był to zasygnalizowany problem testu stopu. Związane z tym problemem jest pytanie drugie – '''czy wygenerowany ciąg''' w ogóle '''jest zbieżny''', a gdy jest, to '''czy jego granica jest rozwiązaniem zadania optymalizacji ?''' Jest to pytanie teoretyczne i odpowiemy na nie po konkretyzacji algorytmu w wykładzie siódmym. | ||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width=" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd22.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd22.png|thumb|500px]] | ||
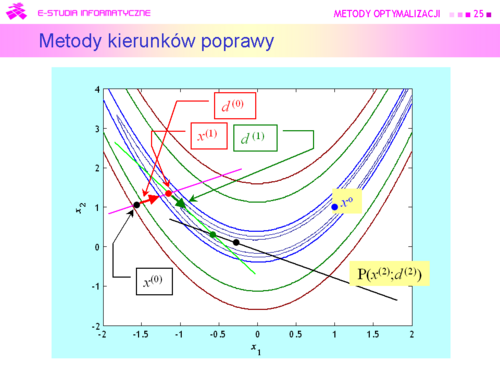
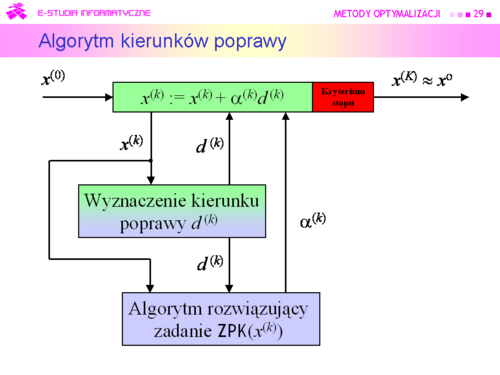
|valign="top"|Tu oczywistym pomysłem jest wykorzystanie rozważań teoretycznych, pokazujących związek kierunku poprawy z gradientem (lemat 4.3). | |valign="top"|Tu oczywistym pomysłem jest wykorzystanie rozważań teoretycznych, pokazujących związek kierunku poprawy z gradientem (lemat 4.3). | ||
Algorytm będzie zatem wykorzystywał: | Algorytm będzie zatem wykorzystywał: | ||
'''Metody kierunków poprawy''' | '''Metody kierunków poprawy''' | ||
Wersja z 12:27, 4 paź 2006
 |
 |
 |
 |
 |
Algorytm może być:
a następnie przeszukiwać je tak jak poprzednio. |
 |
 |
Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm wymyślony przez:
J. A. Neldera i R. Meada i opublikowany w 1965 r. |
 |
Dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo ładnie. |
 |
Metody oparte na takim rozumowaniu od połowy lat dziewięćdziesiątych XX w nazywa się:
Metodami obszaru zaufania (Trust region methods) |
 |
 |
 |
Tu oczywistym pomysłem jest wykorzystanie rozważań teoretycznych, pokazujących związek kierunku poprawy z gradientem (lemat 4.3).
Algorytm będzie zatem wykorzystywał: Metody kierunków poprawy |
 |
 |
 |
 |
Teraz zauważmy tylko, że test stopu powinien zawierać dwa warunki: jeden badający “optymalność” kolejnego punktu, a drugi określający maksymalną liczbą iteracji. |
 |
 |
 |
 |
 |
 |