GKIW Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 120: | Linia 120: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_16.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_16.png|400px]] | ||
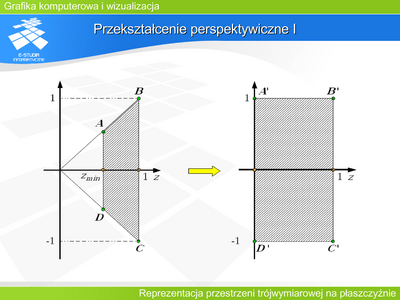
|valign="top"| | |valign="top"|Przekształcenie perspektywiczne I | ||
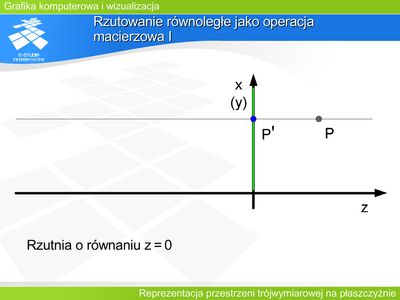
Zaproponowane macierze rzutowania, zarówno perspektywicznego jak równoległego mają jedną zerową kolumnę lub wiersz. Oznacza to że nie jest możliwe wyznaczenie macierzy odwrotnej. Czyli nie jest możliwe odtworzenie trzeciego wymiaru tylko i wyłącznie na podstawie rzutu obiektu. Oczywiście jest to zgodne definicją rzutowania: rzutem całej prostej rzutującej jest dokładnie jeden punkt. | |||
Często do następnych operacji (na przykład do eliminacji elementów zasłoniętych) niezbędna jest informacja o trzecim wymiarze (odległości od obserwatora - głębokości). Rozwiązanie tego problemu przynosi przekształcenie perspektywiczne. Jest to operacja, która pozwala wyznaczyć rzut perspektywiczny i jednocześni daje informację o odległości. | |||
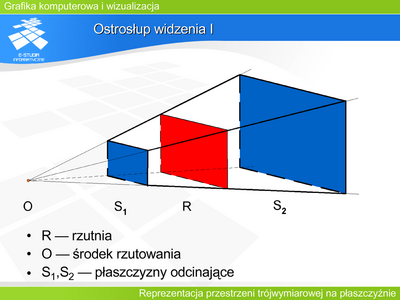
Jeśli rozpatrzymy znormalizowaną bryłę widzenia perspektywicznego – ostrosłup ścięty, to promienie rzutujące tworzą pęk prostych w wierzchołku tego ostrosłupa. Można dokonać przekształcenia, które przekształci ostrosłup ścięty na prostopadłościan. Wtedy pęk prostych (promieni rzutujących) stanie się zbiorem prostych równoległych. A to oznacza, że po takim zniekształceniu przestrzeni wszystkie punkty leżące na prostej rzutującej będą miały jednakowe współrzędne odpowiadające współrzędnym rzutu. | |||
|} | |} | ||
| Linia 127: | Linia 133: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_17.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_17.png|400px]] | ||
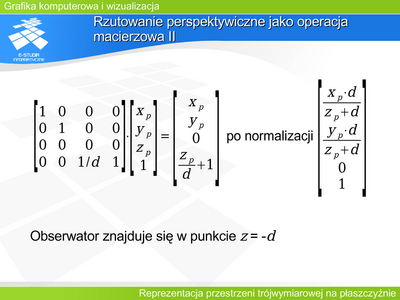
|valign="top"| | |valign="top"|Przekształcenie perspektywiczne II | ||
Macierz przekształcenia perspektywicznego wymaga normalizacji operacji. Wynik na rysunku jest podany z uwzględnieniem normalizacji. | |||
Jak widać współrzędne x i y obrazu punktu odpowiadają współrzędnym rzutu perspektywicznego przy założeniu, że środek rzutowania jest w początku układu współrzędnych. Jednocześnie współrzędna z obrazu daje informację o położeniu względem osi OZ. Warto zwrócić uwagę na fakt, że przekształcenie wartości głębokości jest operacją nieliniową, ale zachowującą porządek na prostej, co w zupełności wystarcza do oceny głębokości. | |||
|} | |} | ||
| Linia 134: | Linia 145: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_18.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_18.png|400px]] | ||
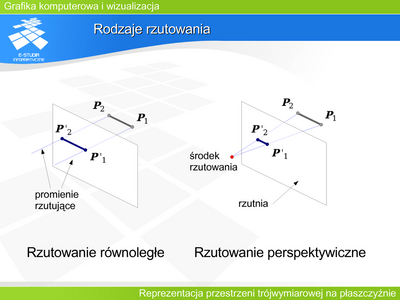
|valign="top"| | |valign="top"|Rzutowanie a fotografia, wirtualna kamera | ||
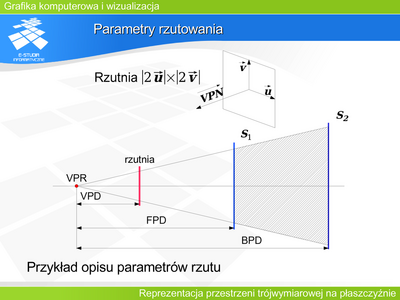
Translacja obiektu kamery w układzie współrzędnych świata, odpowiadająca przesuwaniu aparatu w dowolnym kierunku (przemieszczanie się fotografa). | |||
Obroty wokół osi własnego układu współrzędnych kamery, pozwalające symulować skierowanie aparatu w dowolnie wybranym kierunku. | |||
Zmiany kątów ostrosłupa widzenia np. poprzez definicję odległości rzutni o zadanym prostokącie obrazu od środka rzutowania (obserwatora). Odpowiada to zmianie ogniskowej (kąta „widzenia”) obiektywu. | |||
Związanie definicji kształtu ostrosłupa widzenia i obrotów z własnym układem współrzędnych wirtualnej kamery zapewnia wygodę manipulacji oraz zgodność symulacji z rzeczywistością. | |||
|} | |} | ||
| Linia 141: | Linia 158: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_19.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_19.png|400px]] | ||
|valign="top"| | |valign="top"|Ostrość w rzutowaniu | ||
Parametrem aparatu fotograficznego, o którym nie było dotychczas mowy, jest ostrość. Parametr ten nie daje się w prosty sposób przenieść na opis rzutowania. Ostrość zdjęcia jest wynikiem zależności między właściwościami optycznymi obiektywu, a odległością obiektu od obiektywu. Rzutowanie natomiast odwzorowuje wszystkie obiekty w sposób ostry. Niestety, nie jest to zaletą wirtualnej kamery, jeśli obraz ma być zgodny z naszym widzeniem, gdyż akomodacja oka powoduje powstanie widocznych sfer ostrości. Szczególnie jest to niekorzystne w sytuacji wykorzystywania grafiki komputerowej w kinematografii, gdzie nieostrość danego obiektu może być zamierzonym efektem reżysera. | |||
Rzeczywisty obiektyw aparatu daje ostry obraz punktu w dokładnie określonym miejscu – na płaszczyźnie powstawania obrazu. Zarówno bliżej jak i dalej obrazem punktu jest plamka rozproszenia (rozmyte koło) – stąd nieostry obraz. Analizę zjawiska przeprowadził Lommel w końcu XIX wieku. Zaproponował on pewne uproszczenia stosowane w opisie ostrości do dzisiaj.: | |||
- Plamka rozproszenia ma średnicę wprost proporcjonalną do odległości między płaszczyzną, na której powstała, a płaszczyzną ostrego obrazu. | |||
- Wewnątrz plamki rozproszenia jasność jest w przybliżeniu odwrotnie proporcjonalna do odległości od środka plamki. W przybliżeniu, gdyż w środku plamki jasność ma pewną skończoną wartość, natomiast na brzegu plami (w skończonej odległości równej promieniowi plamki) maleje do zera. | |||
- Zmiana ostrości nie powoduje zmian jasności całego obrazu, tylko zmianę rozkładu jasności. | |||
Stosowanym rozwiązaniem jest sztuczne rozmycie symulujące nieostrość w wybranych fragmentach obrazu. Dokonuje się tego albo stosując bufor akumulacji albo odpowiednie filtrowanie. Więcej na ten temat zainteresowani mogą przeczytać w pracy: Rokita P.: Problemy łączenia obrazów generowanych metodami grafiki komputerowej z obrazami rzeczywistymi. Prace naukowe. Elektronika. Politechnika Warszawska 2001. | |||
|} | |} | ||
| Linia 148: | Linia 173: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_20.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_20.png|400px]] | ||
|valign="top"| | |valign="top"|Wirtualne studio I | ||
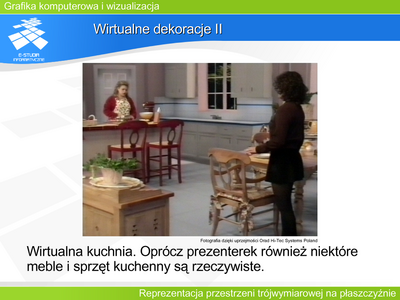
Umieszczenie w wyimaginowanym świecie wirtualnej kamery, która daje możliwość manipulacji zgodnie ze znanymi realiami pozwala łączyć obrazy rzeczywiste z wirtualnymi. Przykładem takiego „graficznego świata” jest wirtualne studio, coraz częściej wykorzystywane przez stacje telewizyjne. Zamiast budować dekoracje do nowego programu, tworzy się je za pomocą grafiki komputerowej. Program powstaje w ten sposób, że niezależnie prowadzi się dwie rejestracje. Rejestrację prezenterów (lub innych osób występujących) rzeczywistą kamerą oraz „rejestrację” wirtualnej dekoracji wirtualną kamerą. Obie kamery mają odpowiednio zgodne parametry funkcjonalne oraz w pełni zsynchronizowane ruchy. Oba obrazy składa się następnie techniką blue boxu, tworząc to, co potem oglądamy na ekranie. Oczywiście możliwe są dowolne warianty łączenia elementów rzeczywistych i wirtualnych łącznie z dowolnym zasłanianiem jednych przez drugie. | |||
Technika ta pozwala zaoszczędzić nie tylko pieniądze, czas i materiały przy tworzeniu dekoracji, pozwala też „zaoszczędzić” powierzchnię studia telewizyjnego, gdzie odbywa się realizacja programu. Oglądając program wierzymy w masywne dekoracje rozstawione na olbrzymiej przestrzeni, a w rzeczywistości prezenter może siedzieć w ciasnym wnętrzu. | |||
Zainteresowanych tematem wirtualnego studia zachęcamy do przeczytania pracy: Wojdała A., Gruszewski M., Olech R.: Real-Time Shadow Casting in Virtual Studio. Machine Graphics & Vision IPI PAN vol. 9, nos.1/2, 2000, ss.315-329. | |||
|} | |} | ||
Wersja z 21:41, 30 wrz 2006

|

|

|
|

|
|
|
|
|
|
|

|
|

|
|
|

|
|
|

|