MO Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 49: | Linia 49: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M4_Slajd9.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M4_Slajd9.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Z rozważań geometrycznych wiadomo, że iloczyn skalarny dwu wektorów jest ujemny wtedy gdy kąt miedzy nimi jest rozwarty. Tak też jest na rysunku dla wybranego wektora d. | ||
|} | |} | ||
---- | ---- | ||
| Linia 121: | Linia 121: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M4_Slajd21.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M4_Slajd21.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Uwaga: intuicyjnie wydaje się, że tezy powinny być zamienione miejscami! Konieczność sformułowania jak w lemacie wynika z faktu, że dla macierzy zerowej 0 mamy dla każdego <math>x: x^T0x^T = 0 \ge 0</math>, zatem macierz ta jest dodatnio (i ujemnie też!) półokreślona. | ||
|} | |} | ||
---- | ---- | ||
| Linia 277: | Linia 277: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M4_Slajd47.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M4_Slajd47.png|thumb|500px]] | ||
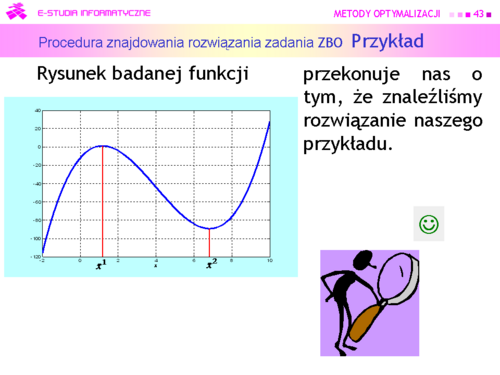
|valign="top"| | |valign="top"|Zatem, dla funkcji dostatecznie gładkich możemy sobie poradzić z zagadnieniem punktu szóstego procedury (teraz powinno być jasne, dlaczego jest tam wstawiona uwaga „gdy wiemy, że nasze zadanie ma rozwiązanie”). | ||
|} | |} | ||
---- | ---- | ||
| Linia 307: | Linia 307: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M4_Slajd52.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M4_Slajd52.png|thumb|500px]] | ||
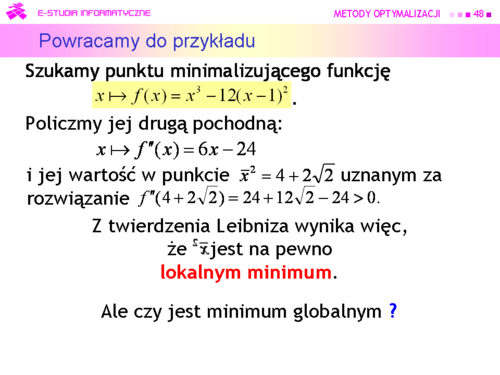
|valign="top"| | |valign="top"|Piękny rezultat teoretyczny, sprowadzający procedurę redukcji do układu równań wyłącznie do rachunków: liczenia pochodnych i rozwiązywania równań, czyli do takiego postępowania, które zastosowaliśmy z ochotą lecz błędnie w przykładzie. Trzeba tylko policzyć macierz Hessego by stwierdzić wypukłość funkcji celu i zastanowić się nad sposobem rozwiązania stosownych równań, ale odpadają zagadnienia związane z dowodem istnienia rozwiązania. | ||
|} | |} | ||
---- | ---- | ||
| Linia 313: | Linia 313: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M4_Slajd53.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M4_Slajd53.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Napisaliśmy, w zasadzie, ponieważ opracowano procedury automatycznego różniczkowania (nie mylić z procedurami symbolicznego różniczkowania), które przetwarzają kod wyliczający funkcję wyboru na kod wyliczający jej pochodne. Zatem wymaganie znajomości wzoru nie jest już takie kategoryczne | ||
|} | |} | ||
---- | ---- | ||
| Linia 319: | Linia 319: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M4_Slajd54.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M4_Slajd54.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Zauważmy, że jednym z plusów tej metody jest to, że idealnie nadaje się do, nazwijmy to tak, sprawdzania wiadomości i zdolności rachunkowych studentów. | ||
|} | |} | ||
---- | ---- | ||
| Linia 385: | Linia 385: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M4_Slajd65.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M4_Slajd65.png|thumb|500px]] | ||
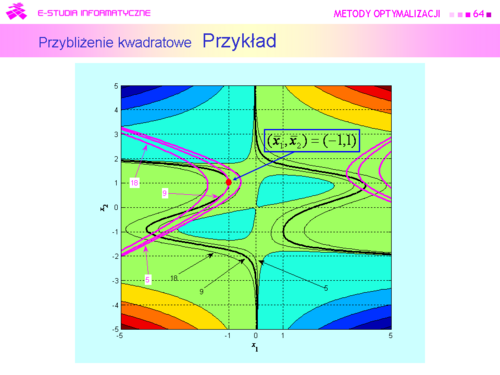
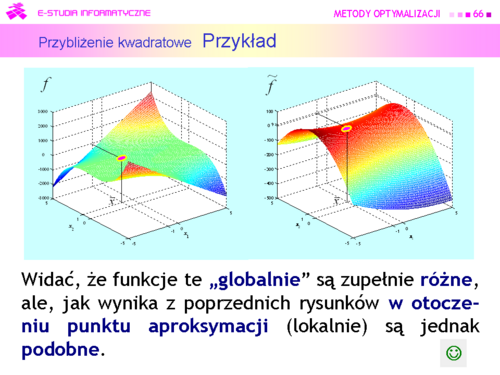
|valign="top"| | |valign="top"|Widać, że otoczenie, w którym aproksymację uznalibyśmy za dobrą nie jest duże i jego kształt jest zbliżony do elipsy o osiach nierównoległych do osi współrzędnych kartezjańskich. | ||
|} | |} | ||
---- | ---- | ||
| Linia 403: | Linia 403: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M4_Slajd68.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M4_Slajd68.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Korzystać z aproksymacji – nie korzystać ?''' | ||
Tego rodzaju dylemat jest typowy dla sytuacji, w której znajduje się twórca no-wych rozwiązań konstrukcyjnych – magister, a więc mistrz – a także twórca nowych teorii naukowych. Za podejściem optymisty opowiedział się Albert Einstein, który stwierdził, że “God is subtle but he is not malicious”. Co w naszym przypadku przekłada się na przeświadczenie, że nieliniowe zadania optymalizacji związane z rozwiązywaniem zagadnień praktycznych, są takie, że zręczne wykorzystanie możliwości jakie daje posługiwanie się aproksymacją (APR) pozwoli opracować skuteczne algorytmy ich rozwiązywania. Współcześni optymiści mają sławnego poprzednika – Izaaka Newtona, który wymyślił metodę stycznych rozwiązywania równań nieliniowych opartą o jeszcze prostszą aproksymację, bo ograniczoną tylko do składnika afinicznego. | |||
|} | |} | ||
---- | ---- | ||
| Linia 415: | Linia 418: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M4_Slajd70.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M4_Slajd70.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Intuicyjnie – dodanie członu afinicznego “przesuwa” formę kwadratową nie zmieniając jej kształtu, tzn. nie zmienia jej podstawowych własności | ||
|} | |} | ||
---- | ---- | ||
| Linia 445: | Linia 448: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M4_Slajd75.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M4_Slajd75.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Wektory własne nie są wyznaczone jednoznacznie''', i nie jest to przypadek. W terminologii używanej w teorii metod optymalizacji wektory własne wyznaczają tylko kierunki (proste). | ||
|} | |} | ||
---- | ---- | ||
| Linia 493: | Linia 496: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M4_Slajd83.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M4_Slajd83.png|thumb|500px]] | ||
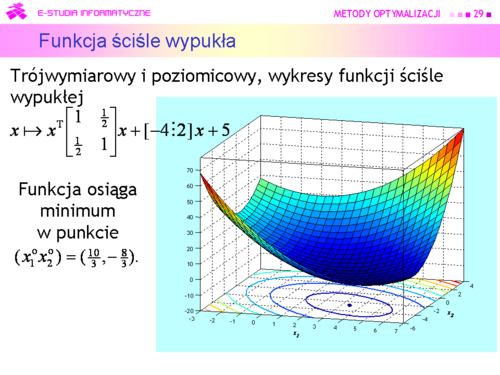
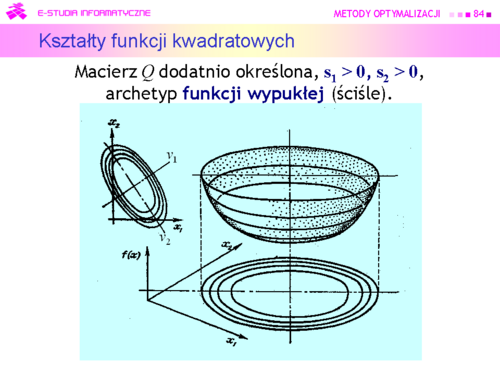
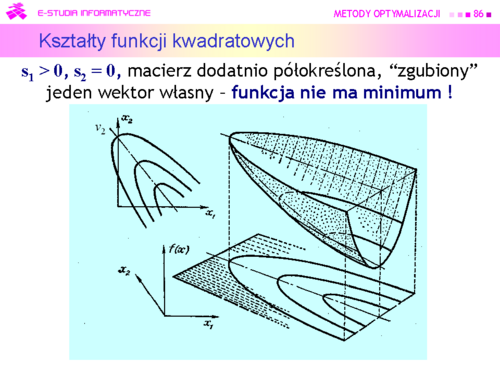
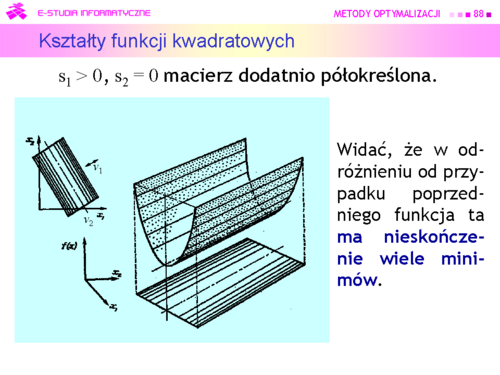
|valign="top"| | |valign="top"|Niestety, możemy narysować tylko funkcję dwu zmiennych (jak często mówimy, na płaszczyźnie). Przedstawmy zatem wykresy trójwymiarowe i poziomicowe dla pierwszych trzech przypadków, ponieważ funkcje określone ujemnie to “odwrócone w dół” funkcje określone dodatnio. | ||
|} | |} | ||
---- | ---- | ||
| Linia 559: | Linia 562: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M4_Slajd94.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M4_Slajd94.png|thumb|500px]] | ||
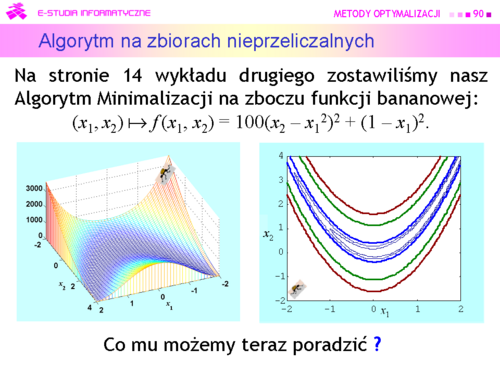
|valign="top"| | |valign="top"|Widać, ze funkcja Rosenbrocka jest dobrze dobrana jako “tor badania sprawności” dla różnych algorytmów. Tylko w centralnej części (tam gdzie nie ma minimum) jej uwarunkowanie jest mniejsze od pięciu, a w okolicy minimum jest większe od 500. | ||
|} | |} | ||
---- | ---- | ||
Wersja z 11:56, 27 wrz 2006
 |
 |
 |
 |
 |
 |
 |
 |
 |
Z rozważań geometrycznych wiadomo, że iloczyn skalarny dwu wektorów jest ujemny wtedy gdy kąt miedzy nimi jest rozwarty. Tak też jest na rysunku dla wybranego wektora d. |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Zauważmy, że jednym z plusów tej metody jest to, że idealnie nadaje się do, nazwijmy to tak, sprawdzania wiadomości i zdolności rachunkowych studentów. |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
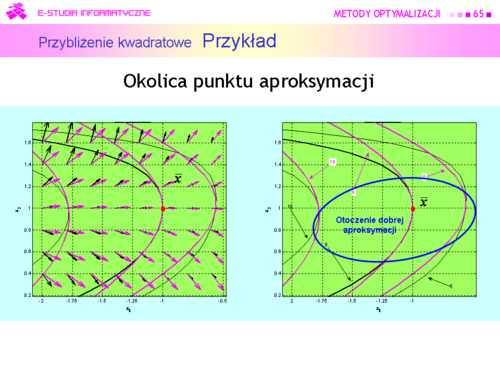 |
Widać, że otoczenie, w którym aproksymację uznalibyśmy za dobrą nie jest duże i jego kształt jest zbliżony do elipsy o osiach nierównoległych do osi współrzędnych kartezjańskich. |
 |
 |
 |
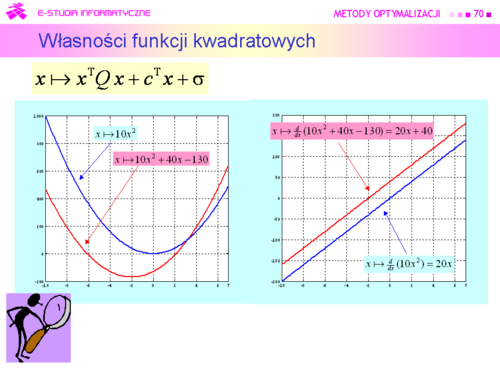 |
Intuicyjnie – dodanie członu afinicznego “przesuwa” formę kwadratową nie zmieniając jej kształtu, tzn. nie zmienia jej podstawowych własności |
 |
 |
 |
 |
 |
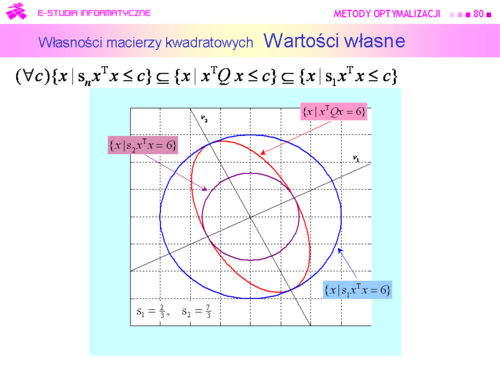
Wektory własne nie są wyznaczone jednoznacznie, i nie jest to przypadek. W terminologii używanej w teorii metod optymalizacji wektory własne wyznaczają tylko kierunki (proste). |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |






