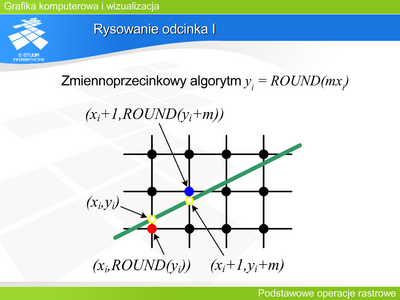
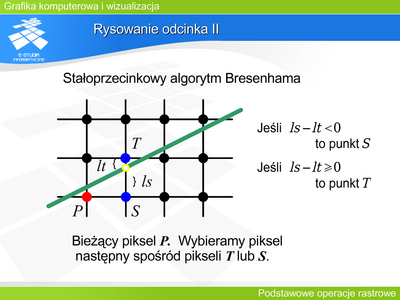
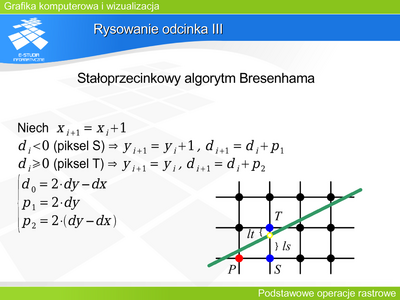
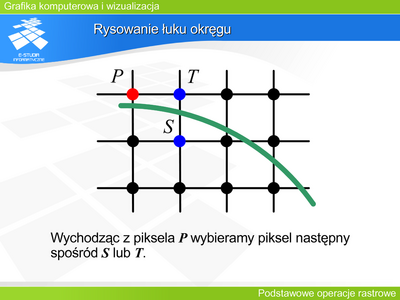
GKIW Moduł 3: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 133: | Linia 133: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd9.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd9.png|400px]] | ||
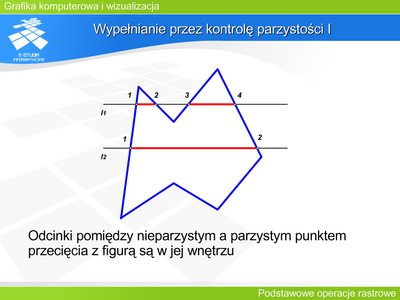
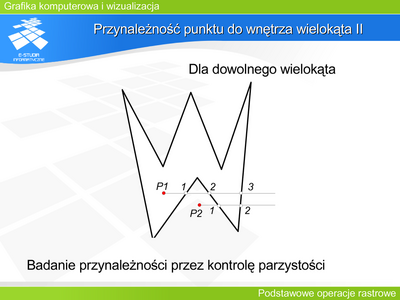
|valign="top"| | |valign="top"|Wypełnianie przez kontrolę parzystości wykorzystuje pewną właściwość przecięcia brzegu linią prostą. Jeśli punkty przecięcia ponumerujemy kolejnymi liczbami naturalnymi zgodnie z orientacją prostej (na rysunku od lewej do prawej dla prostej poziomej) i jeśli będziemy poruszać się po prostej zgodnie z jej orientacją to każde nieparzyste przecięcie będzie „wejściem” do wnętrza obszaru, natomiast każde parzyste będzie „wyjściem” na zewnątrz. Zatem, aby wypełnić obszar należy go przecięć prostymi odpowiadającymi kolejnym rzędom pikseli, a następnie wypełnić odcinkami pomiędzy każdym nieparzystym przecięciem, a najbliższym parzystym. | ||
|} | |} | ||
| Linia 141: | Linia 141: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd10.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd10.png|400px]] | ||
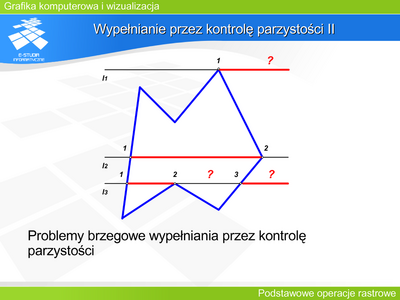
|valign="top"| | |valign="top"|Oczywiście należy zmodyfikować to postępowanie dla przypadków szczególnych, gdy punkt przecięcia jest jednocześnie lokalnym ekstremum brzegu, co zaburza prostą regułę parzystości. Lokalizacja lokalnego ekstremum możliwa jest na podstawie położenia końców przecinanych odcinków. Jeśli są po tej samej stronie prostej wypełniającej – przecinany punkt jest lokalnym ekstremum i nie należy jego liczyć przy analizie parzystości. | ||
Na rysunku prosta l2 przecina wielokąt w wierzchołku (punkt 2) ale jest to przecięcie zwykłe – pozostałe końce przecinanych boków są po przeciwległych stronach prostej l2. Prosta l3 również przecina wielokąt w wierzchołku (punkt 2) ale jest to ekstremum lokalne – pozostałe końce boków są po tej samej stronie prostej l3. | |||
|} | |} | ||
| Linia 148: | Linia 151: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd11.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd11.png|400px]] | ||
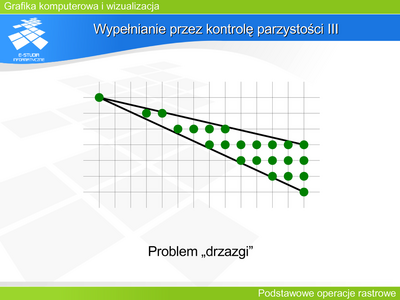
|valign="top"| | |valign="top"|W szczególnych przypadkach mogą pojawić się obszary nie dające się wypełnić w sposób spójny – problem „drzazgi”. Jedynym sposobem rozwiązania tego problemu jest nadpróbkowanie. Należy spróbkować i wypełnić drzazgę z większą rozdzielczością, a następnie uśrednić barwę/luminancję wracając do rozdzielczości rastra. | ||
|} | |} | ||
| Linia 155: | Linia 159: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd12.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd12.png|400px]] | ||
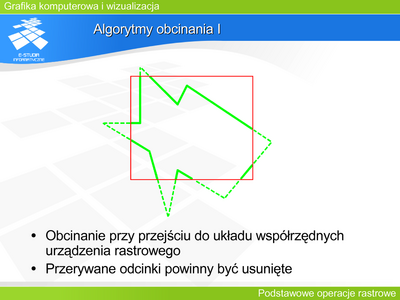
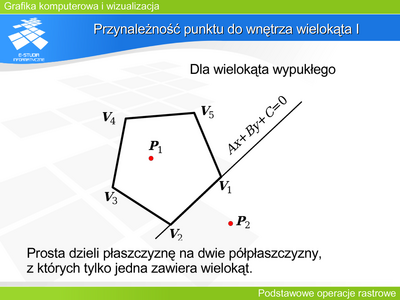
|valign="top"| | |valign="top"|Większość rysowanych obiektów jest definiowana w rzeczywistym układzie kartezjańskim. Przedstawienie takiego obiektu na ekranie monitora (lub z wykorzystaniem innego urządzenia) wymaga określenia fragmentu, który jest obrazowany. Jeśli tylko część prymitywu jest zobrazowana, to oprócz algorytmu rysowania prymitywu jest potrzebny algorytm obcinania go do widocznego fragmentu. | ||
|} | |} | ||
| Linia 162: | Linia 167: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd13.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd13.png|400px]] | ||
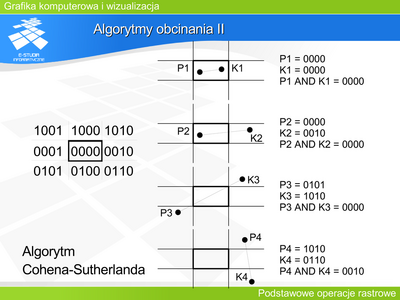
|valign="top"| | |valign="top"|Algorytm Cohena-Sutherlanda (1974) służy do obcinania odcinków do prostokątnego okna. Oznacza to, że należy wybrać odcinki (lub ich fragmenty) do obcięcia na podstawie położenia ich końców. | ||
Płaszczyzna została podzielona na 9 obszarów . Prostokąt centralny odpowiada obszarowi okna. Jednocześnie krawędzie okna wyznaczają cztery proste: prawą, lewą, górna i dolną. Każdemu obszarowi został przypisany czterobitowy kod. Kolejne bity kodu określają poziome i pionowe pasy. Operacja AND przeprowadzona na kodach końców odcinka pozwala odrzucić te odcinki, które na pewno są poza oknem. Spośród pozostałych odcinków należy wybrać te, które rzeczywiście mają wspólne punkty z oknem oraz przyciąć do jego rozmiaru. Operacja AND pozwala w tym przypadku wybrać prostą obcinającą. | |||
Jeśli wynik operacji AND jest różny od zera – należy odrzucić odcinek jako nie mający na pewno punktów wspólnych z oknem. | |||
Jeśli wynik operacji AND jest zerowy – odcinek może przecinać okno. | |||
W takiej sytuacji należy rozważyć przypadek szczególny gdy kody obu końców są zerowe (punkty P1 i K1 na rysunku), wtedy cały rysunek leży wewnątrz okna. | |||
Natomiast jeśli kody końców są niezerowe to określają one którymi prostymi należy przyciąć odcinek. Odcinek <math>\displaystyle \overline{P2P2}\,</math> należy przyciąć prostą prawą (K2=0010). Odcinek <math>\displaystyle \overline{P3P3}\,</math> prostymi lewą i dolną (P3=0101) oraz prawą i górną (K3=1010). | |||
|} | |} | ||
| Linia 169: | Linia 184: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd14.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd14.png|400px]] | ||
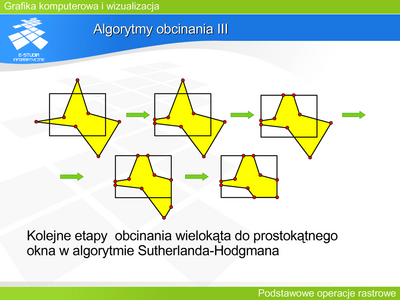
|valign="top"| | |valign="top"|W przypadku obcinania wielokąta, zastosowanie algorytmu obcinania odcinków przynosi tylko połowiczny sukces. Wielokąt tworzy bowiem zbiór uporządkowanych wierzchołków. Każdy wierzchołek jest początkiem pewnego boku i jednocześnie jest końcem poprzedniego boku w danym uporządkowaniu. Potraktowanie boków wielokąta jako zbioru odcinków i przycięcie ich powoduje, że tracimy informacje o ich połączeniach. | ||
Przykładem algorytmu rozwiązującego ten problem jest algorytm Sutherlanda-Hodgmana obcinania wielokąta. | |||
Niech kolejne wierzchołki wielokąta tworzą listę cykliczną | |||
Obcinanie odbywa się kolejno dla prostych zawierających boki okna w ustalonym porządku – np. tak jak na rysunku zgodnie z ruchem wskazówek zegara poczynając od krawędzi lewej. W każdym kroku algorytmu rozpatrywany jest jeden wierzchołek leżący poza oknem przycinania. Wierzchołek taki jest usuwany z listy ale w jego miejsce wstawiane są wierzchołki „odpowiadające mu” na brzegu okna. Oczywiście należy wziąć pod uwagę również i takie przypadki, w których dodany wierzchołek będzie leżał na prostej zawierającej bok okna ale będzie to wierzchołek, który zostanie również usunięty np. w następnym kroku. Z drugiej strony możliwy jest także przypadek, kiedy kolejne wierzchołki wielokąta leżą na zewnątrz okna i wtedy kilka z nich może zostać zastąpionych jednym punktem na brzegu okna. | |||
|} | |} | ||
| Linia 176: | Linia 198: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd15.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd15.png|400px]] | ||
|valign="top"| | |valign="top"|Algorytm Cohena-Sutherlanda bardzo efektywnie klasyfikuje odcinki i jednocześnie jest bardzo prosty w implementacji. Powoduje to, że jest chyba najczęściej stosowanym algorytmem przycinania odcinków do prostokątnego okna. | ||
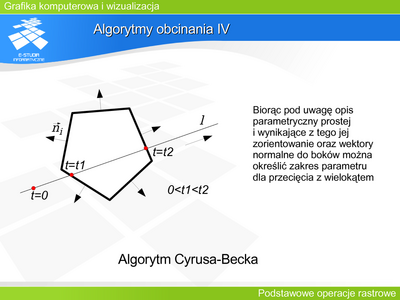
Ma jednak jedną wadę. Często odcinki są przycinane kilka razy (różnymi prostymi) zanim uzyskają końcową postać. Z punktu widzenia wyznaczania przecięcia nie jest to efektywne. W 1978 roku Cyrus i Beck zaproponowali całkowicie inne podejście do problemu obcinania. | |||
Jeśli opiszemy prostą parametrycznie to wzrost parametru określi naturalny zwrot prostej. Niech punkty P0 i Pk odpowiadają odpowiednio parametrom t=0 i t=tk dla k>0. Wektor <math>\displaystyle \overline{P0Pk}\,</math> określa zwrot prostej. Można przeanalizować iloczyn skalarny tego wektora i wektora normalnego (skierowanego na zewnątrz) do boku wielokąta. | |||
Jeśli <math>\displaystyle \overline{P0Pk}\circ \overrightarrow{n}_i>0</math> to parametr tk określa punkt Pk.który może być „maksymalnym” punktem przecięcia z wielokątem (np. punkt dla t=t2 na rysunku). | |||
Jeśli <math>\displaystyle \overline{P0Pk}\circ \overrightarrow{n}_i<0</math> to parametr tk określa punkt Pk.który może być „minimalnym” punktem przecięcia z wielokątem (np. punkt dla t=t1 na rysunku). | |||
Cyrus i Beck zaproponowali efektywny zestaw operacji parametrycznych do analizy całego wielokąta. Algorytm ten został w 1984 roku rozszerzony Lianga i Barsky’ego do ogólnego przypadku 2D obcinania prostymi równoległymi do osi układu współrzędnych oraz 3D obcinania płaszczyznami prostopadłymi do osi układu współrzędnych. | |||
|} | |} | ||
| Linia 183: | Linia 216: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd16.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd16.png|400px]] | ||
|valign="top"| | |valign="top"|Geometria obliczeniowa (ang. computational geometry) jest stosunkowo nową dziedziną informatyki. Z jednej strony jest często traktowana jako narzędzie niezbędne do realizacji algorytmów w grafice komputerowej, z drugiej pozwoliła również wprowadzić do grafiki nowe struktury danych lub je usystematyzować. Niektóre zagadnienia takie jak wyznaczenie wypukłej otoczki zbioru punktów (wypukłej skorupki) albo triangulacja wielokąta stanowią samodzielne problemy geometrii obliczeniowej i Czytelnik może znaleźć ich rozwiązania w podręcznikach z tej dziedziny. | ||
|} | |} | ||
| Linia 190: | Linia 224: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd17.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd17.png|400px]] | ||
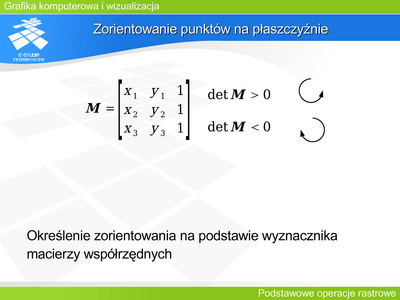
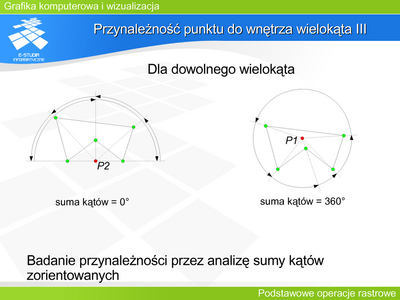
|valign="top"| | |valign="top"|Częstym problemem jest konieczność uporządkowania punktów w układzie biegunowym. Wyznaczenie kąta na podstawie współrzędnych kartezjańskich wymagałoby użycia funkcji trygonometrycznych, co znacznie spowalniałoby rozwiązanie zadania. Funkcja alfa daje możliwość porównania kątów bez wyznaczania ich wartości. Należy jednak pamiętać, że wartość funkcji alfa nie jest liniowo związana z wartością kąta i próba szacowania kąta na tej podstawie byłaby poważnym błędem. | ||
|} | |} | ||
Wersja z 09:45, 27 wrz 2006

|
|
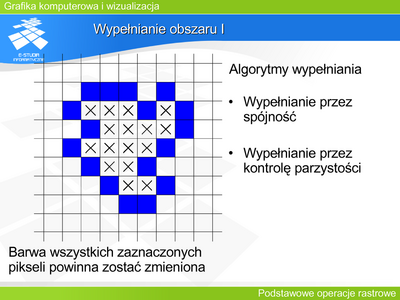
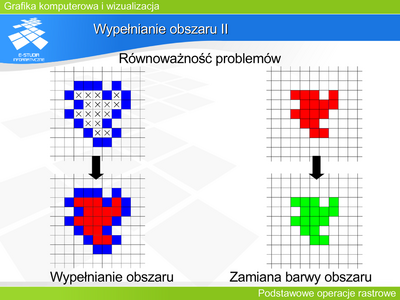
Analogicznym zadaniem do wypełniania obszaru jest zmiana barwy w danym obszarze. Zadania są równoważne. Algorytm rozwiązujący jedno z nich może posłużyć do rozwiązania drugiego. |
|
|
|
|

|