GKIW Moduł 3: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 44: | Linia 44: | ||
:set_pixel(x,y); | :set_pixel(x,y); | ||
:'''while''' (x<xend) '''do begin''' | :'''while''' (x<xend) '''do begin''' | ||
::x := x+1; | |||
::'''if''' (d<0) d := d+p1; | |||
::'''else begin''' | |||
:::d := d+p2; | |||
:::y := y+1; | |||
::'''end''' | |||
::set_pixel(x,y); | |||
:'''end''' | |||
'''end''' | |||
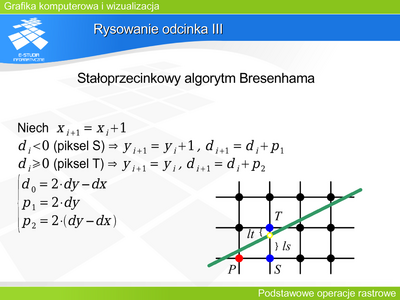
Algorytm taki wykorzystujący tylko operacje całkowite jest również użyteczny w rozwiązaniach sprzętowych. | |||
|} | |} | ||
| Linia 53: | Linia 62: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd4.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd4.png|400px]] | ||
|valign="top"| | |valign="top"|Niestety korzystanie z rastra również i w przypadku rysowania odcinka może prowadzić do pewnych problemów. | ||
Pierwszym jest fakt, że odcinek może nie być symetryczny gdy zamienimy końce startowe. Problem ten wymaga korekty podejmowania decyzji dla d=0 w zależności od wzrostu lub spadku wartości współrzędnych. | |||
Poważniejszym problemem jest zmiana jasności. Oba odcinki na rysunku składają się z 7 punktów. Tylko że odcinek po przekątnej rastra jest <math>\sqrt{2}\,</math> razy dłuższy od odcinka poziomego. Jest to problem związany ze skończoną rozdzielczością rastra i podobnie jak usuwanie wrażenia schodków odcinka rozwiązuje się go zmieniając barwy pikseli sąsiednich. | |||
|} | |} | ||
| Linia 60: | Linia 74: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd5.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd5.png|400px]] | ||
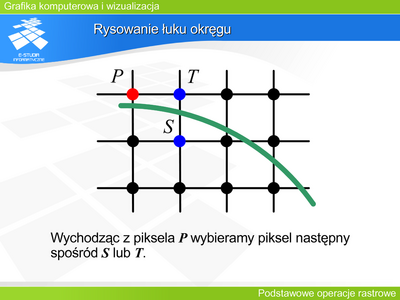
|valign="top"| | |valign="top"|Na podobnej zasadzie jak rysowanie odcinka, Bresenham opracował algorytm rysowania łuku okręgu. Oczywiście zmieniają się w tym przypadku warunki wyboru pikseli, ale algorytm ten również wykorzystuje tylko operacje na liczbach całkowitych. | ||
Przy okazji rysowania okręgu warto zwrócić uwagę na parametr charakteryzujący proporcje boków rastra pikseli w pionie i w poziomie, czyli aspekt. Jeśli proporcje rozdzielczości dla kart graficznych 1024x768 wynoszą 4:3, natomiast 1280x1024 wynoszą 5:4, to jeśli chcemy wyświetlić takie obrazy na tym samym monitorze, to proporcje trzeba przeliczyć także w odległości między pikselami. Inaczej narysowany okrąg albo w jednym albo w drugim przypadku będzie miał kształt elipsy. | |||
|} | |} | ||
| Linia 67: | Linia 84: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd6.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd6.png|400px]] | ||
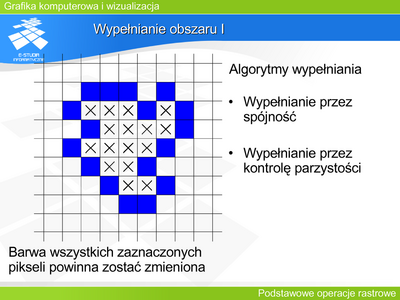
|valign="top"| | |valign="top"|Wypełnianie obszaru jest drugim po rysowaniu odcinka lub łuku, najczęściej występującym problemem związanym z prymitywami. Zadanie dla szczególnych przypadków (np. dla prostokąta) jest zadaniem trywialnym. Natomiast w ogólnym przypadku algorytm powinien pracować poprawnie dla dowolnego wielokąta (także wklęsłego), również dla wielokątów z „dziurami”. | ||
|} | |} | ||
| Linia 74: | Linia 92: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd7.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd7.png|400px]] | ||
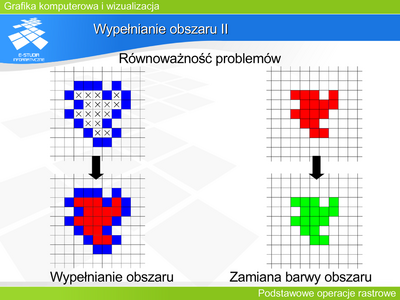
|valign="top"| | |valign="top"|Analogicznym zadaniem do wypełniania obszaru jest zmiana barwy w danym obszarze. Zadania są równoważne. Algorytm rozwiązujący jedno z nich może posłużyć do rozwiązania drugiego. | ||
|} | |} | ||
| Linia 81: | Linia 100: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd8.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd8.png|400px]] | ||
|valign="top"| | |valign="top"|Można zauważyć, że jeśli wybierzemy jeden punkt, który jest wewnątrz wypełnianego obszaru, to punkt sąsiedni będzie również punktem wewnątrz albo będzie punktem brzegowym. | ||
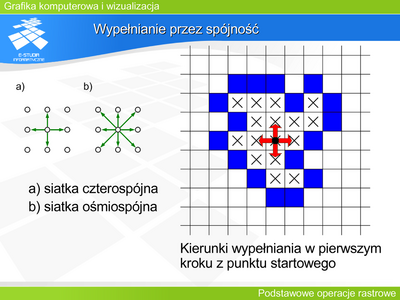
Wypełnianie przez spójność zakłada znajomość punktu startowego (tzw. „ziarna”) wewnątrz obszaru. Punkt ten jest wypełniany, a następnie startując z niego wypełniamy punkty sąsiednie (jeśli oczywiście istnieją – jeśli nie są już wypełnione, ani nie są punktami granicznymi obszaru). Jednocześnie punkty sąsiednie stają się wyjściowymi dla wypełniania w następnym kroku. Procedura ta jest powtarzana dopóki można wskazać punkty wyjściowe (niewypełnione) wewnątrz obszaru. | |||
Warto zwrócić tutaj uwagę na problem sąsiedztwa i konieczność dostosowania do niego kształtu brzegu. Można wyróżnić dwa przypadki. Gdy ruchy po mapie pikseli mogą odbywać się analogicznie do ruchów wieży po szachownicy – wtedy piksel ma 4 sąsiadów – siatka jest czterospójna. Gdy dodamy do tego jeszcze ruchy na ukos (odpowiada to kierunkom ruchów hetmana w szachach), to piksel ma 8 sąsiadów – siatka jest ośmiospójna. Czytelnik może przeanalizować jak powinien wyglądać rozkład pikseli brzegu dla obu przypadków aby stanowił on figurę zamkniętą z punktu widzenia możliwości ruchu. | |||
Algorytm wypełniania przez spójność dla siatki czterospójnej. | |||
Przyjęto: c_b – barwa brzegu, c_f – barwa wypełnienia | |||
'''procedure''' wypełnij1(x,y) | |||
'''begin''' | |||
:set_pixel(x,y,c_f); | |||
:'''if''' (barwa(x-1,y) inna niż c_b i inna niż c_f) wypełnij1(x-1,y); | |||
:'''if''' (barwa(x+1,y) inna niż c_b i inna niż c_f) wypełnij1(x+1,y); | |||
:'''if''' (barwa(x,y-1) inna niż c_b i inna niż c_f) wypełnij1(x,y-1); | |||
:'''if''' (barwa(x,y+1) inna niż c_b i inna niż c_f) wypełnij1(x,y+1); | |||
'''end''' | |||
Czytelnik może zaproponować korektę obejmującą siatkę ośmiospójną. | |||
Zaproponowana postać algorytmu wypełniania przez spójność jest algorytmem rekurencyjnym. Daje to łatwość opisu ale także problemy realizacyjne. Z tego powodu znane są wersje niniejszego algorytmu w postaci nierekurencyjnej. | |||
Algorytm wypełniania przez spójność jest czasem nazywany algorytmem przez sianie (punkt startowy jest „ziarnem”). | |||
|} | |} | ||
| Linia 89: | Linia 134: | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd9.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd9.png|400px]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
Wersja z 09:36, 27 wrz 2006

|
|
Analogicznym zadaniem do wypełniania obszaru jest zmiana barwy w danym obszarze. Zadania są równoważne. Algorytm rozwiązujący jedno z nich może posłużyć do rozwiązania drugiego. |
|
|
|
|
|
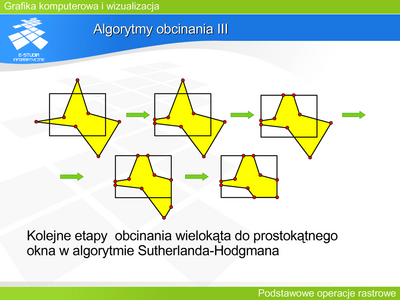
|
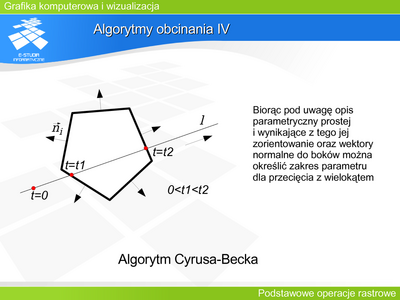
|

|

|
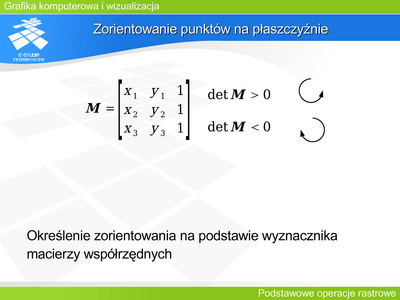
|
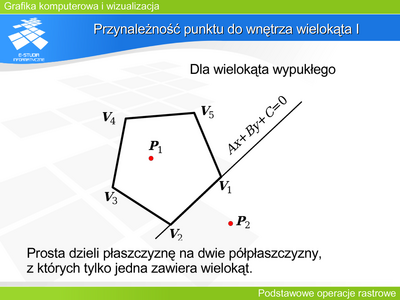
|
|
|

|