GKIW Moduł 3: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 8: | Linia 8: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd0.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd0.png|400px]] | ||
|valign="top"| | |valign="top"|Tworzenie obrazu na monitorze lub urządzeniu drukującym wymaga wypełnienia wybranego obszaru pikseli określonymi barwami w taki sposób, aby powstał zamierzony rysunek. Korzystając z edytora graficznego wybieramy pewne obiekty podstawowe – tak zwane prymitywy (np. odcinek) i żądamy narysowania ich w określonym miejscu. Nie zastanawiamy się w tym momencie nad tym, że żądanie to, z pozoru bardzo proste, wymaga rozwiązanie wielu problemów geometrycznych oraz opracowania skutecznych i szybkich algorytmów. I to bez względu na to czy będzie to realizowane przez odpowiednią bibliotekę czy tez sprzętowo przez kartę graficzną | ||
|} | |} | ||
| Linia 15: | Linia 16: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd1.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd1.png|400px]] | ||
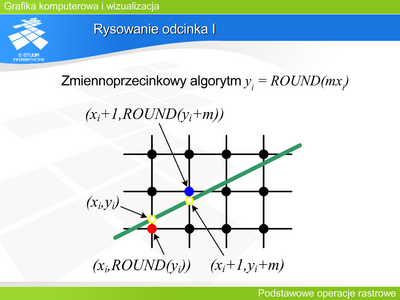
|valign="top"| | |valign="top"|Jednym z podstawowych problemów tego typu jest '''zadanie narysowania odcinka na mapie pikseli'''. Najprostszym rozwiązaniem wydaje się poprowadzenie prostej przez końce odcinka i opisanie jej równaniem <math>y=m\cdot x</math>. Następnie wyznaczenie wartości <math>y_i\,</math> dla całkowitych wartości <math>x_i\,</math> odpowiadających kolejnym kolumnom pikseli. Jeśli teraz przybliżymy współrzędne <math>y_i\,</math> do wartości całkowitej, to otrzymamy współrzędne dla kolejnych pikseli tworzących odcinek tzn. <math>y_i=ROUND(m\cdot x_i)</math> , gdzie <math>ROUND()\,\,</math> jest operacją zaokrąglania do najbliższej wartości całkowitej. Tak skonstruowany algorytm przyrostowy ma podstawową wadę. Wymaga operacji zmiennopozycyjnych (mnożenia, dodawania, zaokrąglania). | ||
|} | |} | ||
| Linia 22: | Linia 24: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd2.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd2.png|400px]] | ||
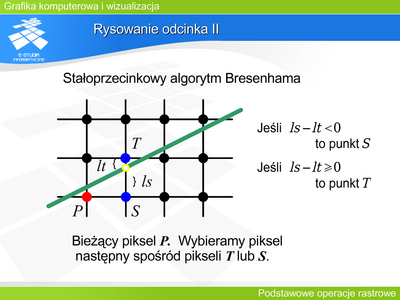
|valign="top"| | |valign="top"|Rozwiązanie oparte w całości na arytmetyce stałopozycyjnej zaproponował Bresenham w 1965 roku. Jest to algorytm przyrostowy, w którym jedna współrzędna np. x wzrasta w każdym kroku o 1, tzn. <math>x_{i+1}=x_i+1</math> . Bez zmniejszania ogólności można przyjąć, że wystarczy opracować algorytm dla nachylenia odcinka od 0 do 1. (Jest to 1/8 układu współrzędnych. Dla innych wartości można bowiem odpowiednio zamienić zmienne lub znaki przed nimi.) Wzrost y w takim przypadku zależy od wyboru piksela (S lub T), który jest bliżej teoretycznej prostej. O wyborze decyduje zmienna kontrolna d, która jest uaktualniana w każdym kroku. | ||
|} | |} | ||
| Linia 29: | Linia 32: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd3.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M3_Slajd3.png|400px]] | ||
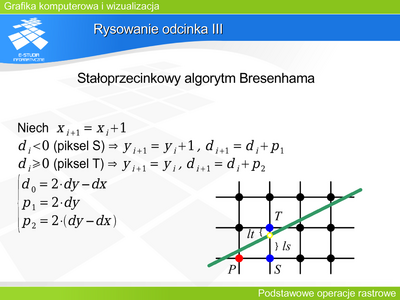
|valign="top"| | |valign="top"|Pełny algorytm Bresenhama dla x2>x1, y2>y1, 0<m<1 wyglądałby tak: | ||
'''procedure Bresline''' (x1,x2, y2,y2,) | |||
'''begin''' | |||
:dx := x2-x1; dy := y2-y1 | |||
:p1 := 2*dy-dx; p2 := 2*(dy-dx); | |||
:x := x1; y := y1; | |||
:xend := x2; | |||
:set_pixel(x,y); | |||
:'''while''' (x<xend) '''do begin''' | |||
|} | |} | ||
Wersja z 09:29, 27 wrz 2006

|

|
|
|
|
|
|
|
|
|
|
|
|

|

|
|
|
|
|

|